Результаты решения задач синтеза управления, обеспечивающего ограниченность на конечном интервале для примера 2-го порядка

Рассмотрим снова пример из п.3.1, в котором вместо конкретной нелинейности присутствует неопределенная нелинейность , удовлетворяющая неравенству (3.2) с параметрами и и . Пусть заданы матрицы 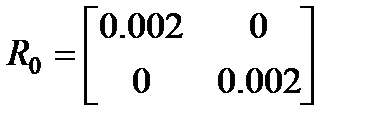, , 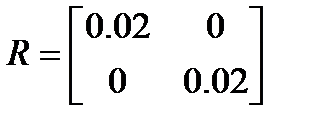определяющие множество 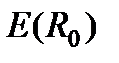начальных отклонений и множество 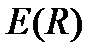допустимых траекторий. На основании теоремы 4 для синтеза управления, обеспечивающего ограниченность относительно заданных множеств 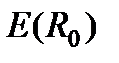, 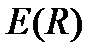была решена задача минимизации следа матрицы Q эллипсоида, ограничивающего выход 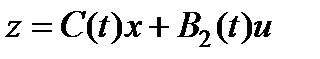при ограничениях (4.4). В результате получены коэффициенты K₂₁=[–7.5929 –25.2643] регулятора и матрица 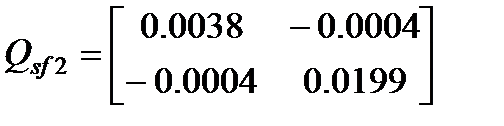инвариантного эллипсоида состояний, минимизирующая след матрицы ограничивающего выход эллипсоида, при следующих значениях параметров: P₁=1, α= 0.1, β₁ =0.0433, g₁ =1. При этих значениях условие (4.5) удовлетворяется на любом заданном интервале, как конечном, так и бесконечном. Поэтому полученный регулятор обеспечивает ограниченность замкнутой системы относительно заданных множеств 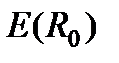и на любом заданном интервале. На рисунке 4.1 представлен переходный процесс в системе с синтезированным регулятором при действии возмущения. Матрица замкнутой системы имеет собственные значения [–0.2264 ± 0.9046i].

Также была решена задача минимизации следа матрицы эллипсоида, ограничивающего выход 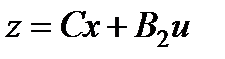при ограничениях (4.4) при заданных P₁=10, g₁ =1, d=1. В результате получены коэффициенты K₂₂=[–3.2964 –10.1826] регулятора и матрица 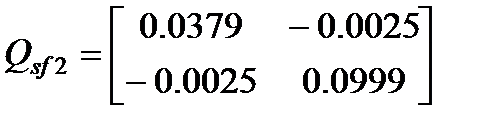инвариантного эллипсоида состояний, минимизирующая след матрицы ограничивающего выход эллипсоида, при следующих значениях параметров: α= 0.1, β₁ = 0.2879. При этих значениях условие (4.5) удовлетворяется при любом заданном интервале, как конечном, так и бесконечном. Полученный регулятор обеспечивает ограниченность замкнутой системы относительно заданных множеств 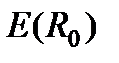и на любом заданном интервале. На рисунке 4.2 представлен переходный процесс в системе с синтезированным регулятором при действии возмущения. Матрица замкнутой системы имеет собственные значения [–0.3347±9.8479].

Рисунок 4.1. Переходный процесс в системе с регулятором K₂₁ с при начальных отклонениях x₀=[5 2] и действии возмущения w=sin(cos(3*t)).

Рисунок 4.2. Переходный процесс в системе с регулятором K₂₂ с при начальных отклонениях x₀=[5 2] и действии возмущения w=sin(cos(3*t)).

Ниже представлен текст программы для синтеза регулятора, обеспечивающего ограниченность замкнутой системы.

%-----модель маятника с неопределенной нелинейностью -------

%-----синтез из условия ограниченности на конечном интервале

%--Исходные данные --

global ABK D CF q bet mu1 F

n=2;n1=n;

w=0.5; mu1=1;

A = [0 1; 0 0];

B1 = [0; 1];

D=[0; 1]/10;

C=[1 0;0 1;0 0];

CF=[1 0]; Bf=[];

R0=eye(2)/500;

S0=eye(2)*0.1;

R=eye(2)/50;

B2=[0; 0;1]/100;

D2=[0; 1;0]/100;

F=[0; -w*w];

% Решение линейных матричных неравенств (Регулятор по состоянию для ограниченности на конечном интервале, стационарный случай)

min_tr_Q=1.e7;

alf=0.1;

gam1=1;

p1=10;

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Ys(1, n1) ;

variable bet1 ;

variable Zs(1,1) symmetric;

% variable gam1;

%variable p1;

minimize( trace(C*Qs*C'+C*Ys'*B2'+B2*Ys*C'+B2*Zs*B2'))

%minimize( trace(Qs))

%minimize( gam1)

subject to

%gam1>0;

Qs >= R0; Qs<=R;

[A*Qs + Qs*A'+B1*Ys+Ys'*B1'+bet1*(F*F')+alf*Qs D*p1 Qs*CF';

p1*D' -gam1*p1 0;

CF*Qs 0 -bet1/mu1]<= 0; %условие асимптотич устойчивости

[Zs Ys;

Ys' Qs]>=0;

cvx_end

Qsf2 = double(Qs)

Y2=double(Ys)

K2=Y2/Qsf2

Z2=double(Zs)

%trZ=trace(C*Qsf2*C'+C*Y2'*B2'+B2*Y2*C'+B2*Z2*B2');

trZ=trace(Qsf2);

ABK2=A+B1*K2;

4.6. Результаты решения задач синтеза управления, обеспечивающего Н_¥ свойство системы 2-го порядка

На основе теоремы 5 при решении задачи 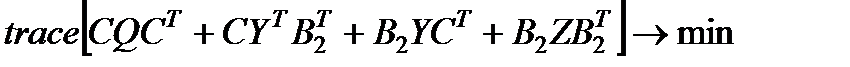с ограничениями (4.20), (4.21) при g=1.9, β=0.05 был получен регулятор с постоянными коэффициентами K₃₁=[–5.0405 –33.5269], обеспечивающий Н_¥ свойство системы (4.16) при всех нелинейностях из (4.17). Матрица обеспечивает минимум следа матрицы ограничивающего эллипсоида для выхода. Матрица замкнутой системы 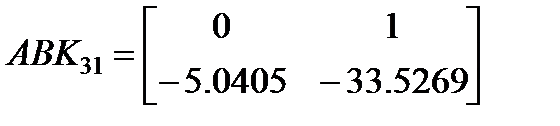имеет собственные значения [–0.1510, –33.3759]. Также при решении той же самой задачи при g=1.2, β=0.1111 был получен регулятор с постоянными коэффициентами K₃₂ =[–11.6575 –15.4229], обеспечивающий Н_¥ свойство системы (4.16) при всех нелинейностях из (4.17). В данном случае матрица 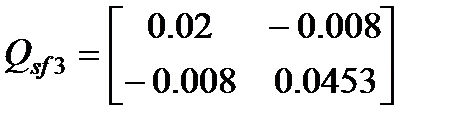. Матрица замкнутой системы 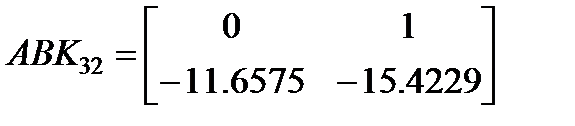имеет собственные значения [-–0.7971, –14.6258]. На рисунках 4.3 и 4.4показаны переходные процессы в исходной нелинейной системе с синтезированными регуляторами K₃₁ и K₃₂ соответственно при действии возмущения w=sin(cos(3*t).

Текст программы синтеза регулятора на основе решения задачи оптимизации следа матрицы при ограничении на степень g подавления начальных отклонений и неопределенных возмущений (на H_¥ критерий качества) представлен ниже.

% Решение линейных матричных неравенств (H-inf Регулятор по состоянию)

gam3=1.2;

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Ys(1, n1) ;

variable bet3 ;

minimize( trace(C*Qs*C'+C*Ys'*B2'+B2*Ys*C'+B2*Zs*B2'))

subject to

Qs >= S0/10/gam3

[A*Qs + Qs*A'+B1*Ys+Ys'*B1'+bet3*(F*F') D Qs*C'+Ys'*B2' Qs*CF';

D' -gam3 D2' 0

C*Qs+B2*Ys D2 -eye(3) zeros(3,1);

CF*Qs 0 zeros(1,3) -bet3/mu1]<= 0; %условие асимптотич устойчивости

[Zs Ys;

Ys' Qs]>=0;

cvx_end

Qsf3 = double(Qs)

Y3=double(Ys)

K3=Y3/Qsf3

ABK3=A+B1*K3

eig(ABK3)

figure(4)

y=Mayat_Integr_01(n1,x0,w,K3,0,50);

-1

t

x1,x2

Рисунок 4.3. Переходный процесс в системе с регулятором K₃₁ с при начальных отклонениях x₀=[5 2] и действии возмущения w=sin(cos(3*t)).

Рисунок 4.4. Переходный процесс в системе с регулятором K₃₂ с при начальных отклонениях x₀=[5 2] и действии возмущения w=sin(cos(3*t))

На основе теоремы 5 при решении задачи с ограничениями (4.20), (4.21) при β=0.0836 был получен регулятор с постоянными коэффициентами K₄=[–34.9030 –82.5244], обеспечивающий Н_¥ свойство системы (4.16) min (g) = 1.0162 при всех нелинейностях из (4.17). При этом матрица . Матрица замкнутой системы 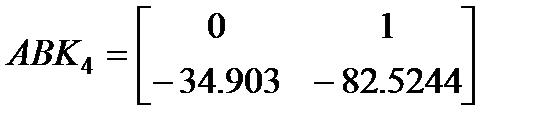имеет собственные значения [–0.4251, –82.0993]. На рисунке 4.5 показан переходный процесс в исходной нелинейной системе с синтезированным регулятором.

Рисунок 4.5. Переходный процесс в системе с регулятором K₄ с при начальных отклонениях x₀=[5 2] и действии возмущения w=sin(cos(3*t))

Ниже представлен текст программы для синтеза регулятора, обеспечивающего минимум g (H_¥ критерию качества).

% Решение линейных матричных неравенств (H-inf Регулятор по состоянию)

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Ys(1, n1) ;

variable bet4 ;

variable gam4;

minimize(gam4)

subject to

Qs >= eye(2)/100;

[A*Qs + Qs*A'+B1*Ys+Ys'*B1'+bet4*(F*F') Qs*CF' D Qs*C'+Ys'*B2';

CF*Qs -bet4/mu1 0 zeros(1,3)

D' 0 -gam4 D2';

C*Qs+B2*Ys zeros(3,1) D2 -eye(3)]<= 0;

cvx_end

Qsf4 = double(Qs)

Y4=double(Ys)

K4=Y4/Qsf4

ABK4=A+B1*K4

eig(ABK4)

figure (5)

y=Mayat_Integr_01(n1,x0,w,K4,0,50);

Также на основе теоремы 5 при решении задачи с ограничениями (4.20), (4.21) на интервале [0,3c] был получен регулятор с зависимыми от времени коэффициентами K(t), обеспечивающий Н_¥ свойство системы (4.16) при всех нелинейностях из (4.17). При этом начальная матрица задавалась как 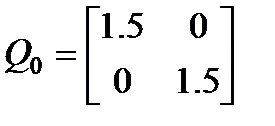. На рисунке 4.6 показаны эллипсы, получаемые в результате решения задачи оптимизации на заданном интервале. Пунктирной линией показан начальный эллипс, сплошными линиями показаны эллипсы, получаемые последовательно на каждом шаге дискретизации при решении задачи оптимизации. Красным цветом показан эллипс, полученный на последнем шаге дискретизации при t=3c. На рисунке 4.7 показаны графики изменения коэффициентов усиления регулятора и параметра β при решении задачи оптимизации на рассматриваемом интервале.

Рисунок 4.6. Эллипсы, получаемые в результате оптимизации следа матрицы эллипса, ограничивающего выход системы

На рисунке 4.8 показаны эллипсы, получаемые в результате решения задачи минимизации g с ограничениями (4.20), (4.21) на заданном интервале. Пунктирной линией показан начальный эллипс, сплошными линиями показаны эллипсы, получаемые последовательно на каждом шаге дискретизации при решении задачи оптимизации. Красным цветом показан эллипс, полученный на последнем шаге дискретизации при t=3c. На рисунках 4.9 и 4.10 показаны графики изменения параметров β, g и коэффициентов усиления регулятора при минимизации g на рассматриваемом интервале.

Рисунок 4.7. Изменение коэффициентов усиления регулятора и параметра β при решении задачи оптимизации на интервале [0,3c]

Для синтеза регулятора на основе решения задачи 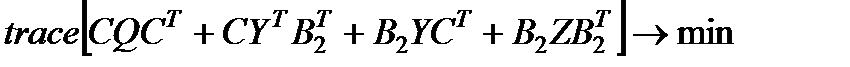с ограничениями (4.20) (на H_¥ критерий качества) и (4.21) на интервале [0,3c] использовалась программа, текст которой представлен ниже.

% Решение дифференциальных линейных матричных неравенств (Регулятор по состонию)

k=1; kend=31; e=0.1;

alf=0.1; t(k)=0; Q0=R+eye(2)/2;

figure (6)

KK1=[];KK2=[];betk=[];

while k<kend

E = ellipsoid(Q0);

% pEs = projection(E, BB);

plot(E, 'b');grid on;hold on;

t(k)=(k-1)*e;

Rt=eye(2)/(100*e);

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Zs;

variable Ys5(1, n1) ;

variable bet5 ;

minimize( trace(C*(Q0-Qs*e)*C'+C*Ys5'*B2'+B2*Ys5*C'+B2*Zs*B2'))

subject to

(Q0-Qs*e)>=eye(2)*1e-6;

Qs>=Q0*e/2;

[Qs+A*(Q0-Qs*e) + (Q0-Qs*e)*A'+B1*Ys5+Ys5'*B1'+bet5*(F*F') D (Q0-Qs*e)*CF';

D' -1/(1+d) 0

CF*(Q0-Qs*e) 0 -bet5/mu1]<= 0; %условие асимптотич устойчивости

[Zs Ys5;

Ys5' (Q0-Qs*e)]>=0;

cvx_end

Qsf5 = double(Qs);

Y5=double(Ys5);

bet05=double(bet5);

betk(k)=bet05;

Q0=Q0-Qsf5*e

E = ellipsoid(Q0);

plot(E, 'b');grid on;hold on;

K5=Y5/Q0;

KK1(k)=K5(1);

KK2(k)=K5(2);

ABK5=A+B1*K5;

tk=k*e

k=k+1;

end;

E = ellipsoid(Q0);

plot(E, 'r');grid on;hold on;

figure (7)

plot(t,betk,'r');grid on;hold on;

plot(t,KK1,'b');grid on;hold on;

plot(t,KK2,'p');grid on;hold on;

Рисунок 4.8. Эллипсы, получаемые в результате минимизации g на интервале [0,3c]

Рисунок 4.9. Изменение коэффициентов усиления регулятора и параметров β и g при решении задачи минимизации g на интервале [0,3c]

Рисунок 4.10. Изменение коэффициентов усиления регулятора при решении задачи минимизации g на интервале [0,3c]

Для синтеза регулятора на основе решения задачи минимизации g (H_¥ критерия) с ограничениями (4.20), (4.21) на заданном интервале использовалась программа, текст которой представлен ниже.

% Синтез управления по H inf критерию с помощью ДЛМН

k=1;

kend=31;

e=0.1;

alf=0.1;

t(k)=0;

figure (8)

Q06=Qsf4+eye(2)/20;

KK1=[];KK2=[]; betk=[];gm=[];t=[];

while k<kend

E = ellipsoid(Q06);

% pEs = projection(E, BB);

plot(E, 'b');grid on;hold on;

t(k)=(k-1)*e;

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Ys(1, n1) ;

variable bet6 ;

variable gam6;

minimize(gam6)

subject to

Qs >= eye(2)*1e-8;

Q06>=Qs*e;

[Qs+A*(Q06-Qs*e)+(Q06-Qs*e)*A'+B1*Ys+Ys'*B1'+bet6*(F*F') (Q06-Qs*e)*CF' D (Q06-Qs*e)*C'+Ys'*B2';

CF*(Q06-Qs*e) -bet6/mu1 0 zeros(1,3);

D' 0 -gam6 D2';

C*(Q06-Qs*e)+B2*Ys zeros(3,1) D2 -eye(3)]<= 0;

cvx_end

Qsf6 = double(Qs);

Y6=double(Ys);

bet06=double(bet6);

betk(k)=bet06;

Q06=Q06-Qsf6*e

K6=Y6/Q06;

gm(k)=gam6;

KK1(k)=K6(1);

KK2(k)=K6(2);

ABK6=A+B1*K6;

tk=k*e

k=k+1;

end;

E = ellipsoid(Q06);

plot(E, 'r');grid on;hold on;

figure (9)

plot(t,KK1,'b');grid on;hold on;

plot(t,KK2,'p');grid on;hold on;

figure (10)

plot(t,betk,'r');grid on;hold on;

plot(t,gm,'g');grid on;hold on;