Реакция на произвольное воздействие

Для решения дифференциального уравнения (нахождения реакции системы) с помощью преобразования Лапласа необходимо:

- найти корни характеристического уравнения ;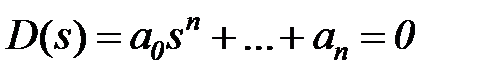

- найти изображение реакции умножением ПФ на изображение входа по Лапласу Y(s) = W(s)×X(s) и записать его в виде суммы простых дробей по теореме разложения в соответствии с корнями характеристического уравнения;

- найти коэффициенты числителей дробей (вычеты в полюсах);

- найти оригинал для каждой дроби по таблице соответствия и запи­сать конечное решение в виде суммы отдельных оригиналов.

Рекомендуется:

а) перед вычислением корней обязательно нормировать ПФ по старшему коэффициенту при sⁿ знаменателя;

б) не сокращать существующие нули и полюса с положительной действительной частью, ведущие к неустойчивости системы, если их части не являются целыми числами; остальные нули и полюса могут быть сокращены перед переходом во временную область;

в) для кратных полюсов записывать дробями все степени корня от наибольшей до первой в порядке их убывания;

г) комплексные сопряженные корни представлять одним общим квадратным трехчленом.

После разложения на простые дроби и вычисления вычетов по­лезно проверить правильность результата. Первое правило проверки – сумма дробей правой части должна быть равна изображению в левой части равенства. Второе правило проверки – сумма всех составляю­щих оригинала при t = 0 (начальное значение оригинала) в соответст­вии со свойствами преобразования Лапласа должна быть равна .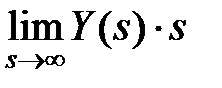

Пример 1. Используя преобразование Лапласа, найти оригинал реакции на воздействие e^–2t системы с ПФ W(s) = 4e^-s/(s + 2). Находим изображение по Лапласу входного воздействия X(s) = 1/(s + 2), умножаем его на передаточную функцию системы, получаем изображение реакции

.

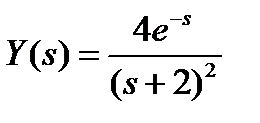При переходе от изображения к оригиналу коэффициент 4 сохраняется, полюс -2 образует составляющую e^–2t, а поскольку он кратный (два одинаковых корня), то появляется составляющая t, и, наконец, оператор сдвига e^–sτ при τ = 1 с создаёт запаздывание во времени, которое отображается скачком со сдвигом вида 1(t – τ) или, в данном случае, 1(t – 1). Окончательно оригинал равен y(t) = 4te^–2t×1(t – 1).

Пример 2. Найти начальное, конечное значения и аналитическую запись для оригинала, если изображение по Лапласу отклика системы равно F(s) = 3/s/(s + 1).

Начальное значение оригинала (при t = 0₊) вычисляется как предел 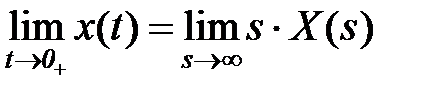, для производной по времени n-го порядка от функции x(t) производится умножение изображения на sⁿ⁺¹, т.е. 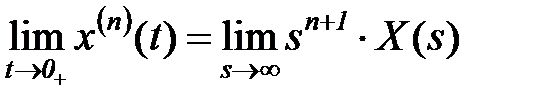. Поэтому

.

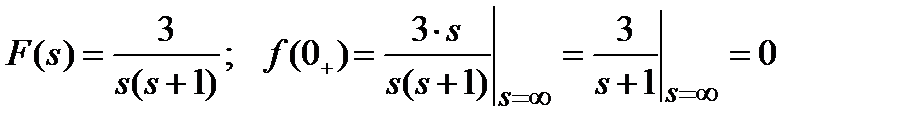Конечное значение оригинала (при t = ∞) для устойчивых систем также вычисляется как предел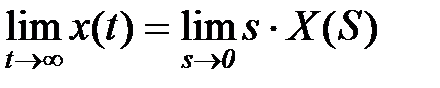

.

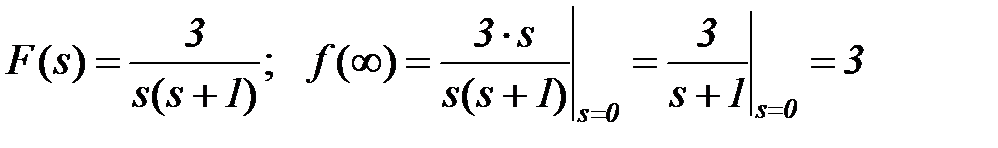Для полной записи оригинала разлагаем изображение на простые дроби в соответствии с полюсами, находим вычеты a и b в полюсахметодом подстановки полюсов (приложение Б)

.

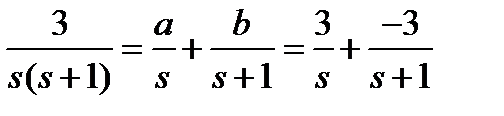По таблице соответствия оригиналов и изображений (приложение А) записываем оригинал в виде формулы f(t) = 3 – 3e^–t. Проверка: при t = 0 значение оригинала равно нулю, при t = ∞ соответственно 3.