Время жизни как случайная величина
В основе страхования жизни, как и любого другого вида страхования, лежит принцип распределения убытков одного лица, с которым произошел страховой случай, на большое число участников страхования, с которыми в рассматриваемый момент времени такой случай не произошел. Неопределенность момента смерти является основным фактором риска при страховании жизни. Относительно момента смерти отдельного человека нельзя сказать ничего определенного. Однако если участники страхования представляют собой большую однородную группу людей, и мы не интересуемся судьбой отдельных людей из этой группы, то в этом случае применим аппарат теории вероятностей как науки о массовых случайных явлениях, обладающих свойством устойчивости. Тогда продолжительность жизни можно рассматривать как случайную величину 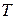 .
.
Функция выживания
В теории вероятностей распределение случайной величины 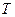 описывается функцией распределения
описывается функцией распределения 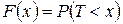 .
.
В актуарной математике принято работать не с функцией распределения, а с дополнительной функцией распределения 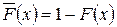 . Применительно к продолжительности жизни
. Применительно к продолжительности жизни 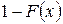 – это вероятность того, что человек доживет до возраста
– это вероятность того, что человек доживет до возраста  лет.
лет.
Функция
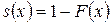
называется функцией выживания: 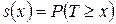 .
.
Функция выживания обладает следующими свойствами:
1. 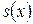 убывает (при
убывает (при 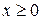 );
);
2. 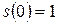 ;
;
3. 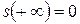 ;
;
4. 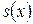 непрерывна.
непрерывна.
Одним из источников данных, необходимых для проведения актуарных расчетов по страхованию жизни, являются таблицы продолжительности жизни. Эти таблицы составляются по данным о смертности населения и о его возрастном составе. В таблицах продолжительности жизни обычно считают, что существует некоторый предельный возраст 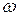 (как правило
(как правило 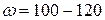 ) и соответственно
) и соответственно 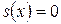 при
при 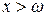 . При описании смертности аналитическими законами обычно считают, что время жизни неограниченно, однако подбирают вид и параметры законов так, чтобы вероятность жизни свыше некоторого возраста была ничтожно мала.
. При описании смертности аналитическими законами обычно считают, что время жизни неограниченно, однако подбирают вид и параметры законов так, чтобы вероятность жизни свыше некоторого возраста была ничтожно мала.
Функция выживания имеет простой статистический смысл. Допустим, производится наблюдение за группой из 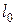 новорожденных (как правило
новорожденных (как правило 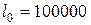 ) и имеется возможность фиксировать моменты их смерти. Обозначим число живых представителей этой группы в возрасте
) и имеется возможность фиксировать моменты их смерти. Обозначим число живых представителей этой группы в возрасте  через
через 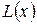 . Тогда
. Тогда
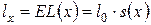 .
.
Таким образом, функция выживания 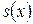 равна средней доле доживших до возраста
равна средней доле доживших до возраста  из некоторой фиксированной группы новорожденных.
из некоторой фиксированной группы новорожденных.
В актуарной математике часто работают не с функцией выживания 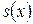 , а с величиной
, а с величиной 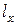 (зафиксировав начальный размер группы
(зафиксировав начальный размер группы 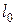 ).
).
Кривая смертей
В теории вероятностей непрерывную случайную величину удобнее описывать плотностью распределения 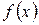 . В актуарной математике график плотности продолжительности жизни
. В актуарной математике график плотности продолжительности жизни 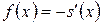 (или, что практически то же, график функции
(или, что практически то же, график функции 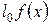 ) называют кривой смертей.
) называют кривой смертей.
Величина 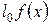 имеет простой статистический смысл. Рассмотрим среднее число представителей исходной группы в
имеет простой статистический смысл. Рассмотрим среднее число представителей исходной группы в 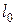 новорожденных, умерших в возрасте
новорожденных, умерших в возрасте  лет. Эта величина обозначается
лет. Эта величина обозначается  и равна
и равна 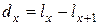 . Тогда
. Тогда 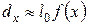 .
.
Функция выживания 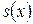 может быть восстановлена по плотности:
может быть восстановлена по плотности:
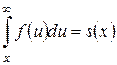 ,
,
так что кривая смертей может быть использована в качестве первичной характеристики продолжительности жизни.
Интенсивность смертности
Величина
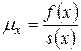
называется интенсивностью смертности. Для человека, дожившего до  лет, при малых
лет, при малых  величина
величина 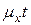 приближенно выражает вероятность смерти в интервале
приближенно выражает вероятность смерти в интервале 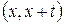 .
.
Поскольку функция выживания 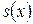 может быть восстановлена по интенсивности смертности:
может быть восстановлена по интенсивности смертности:
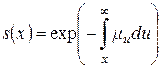 ,
,
то интенсивность смертности может быть использована в качестве первичной характеристики продолжительности жизни.
Макрохарактеристики продолжительности жизни
С практической точки зрения важны следующие макрохарактеристики смертности:
1. среднее время жизни
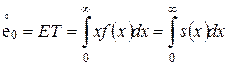 ,
,
2. дисперсия времени жизни
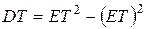 ,
,
где 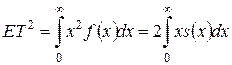 ,
,
3. медиана времени жизни 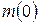 , которая определяется как корень уравнения
, которая определяется как корень уравнения
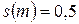 .
.
Медиана времени жизни – это возраст, до которого доживает ровно половина представителей исходной группы новорожденных.
Аналитические законы смертности
Во многих случаях для упрощения расчетов, теоретического анализа и т.п. удобнее описать эмпирические функции выживания или интенсивности смертности с помощью аналитических законов. Преимуществом аналитических законов является то, что для них вероятностные характеристики продолжительности жизни можно быстро вычислять по небольшому числу параметров. А также использовать в случаях, когда доступные данные немногочисленны.
Простейшее приближение было введено в 1729г. де Муавром, который предложил считать, что время жизни равномерно распределено на интервале 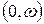 , где
, где 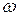 – предельный возраст. В модели де Муавра при
– предельный возраст. В модели де Муавра при 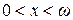
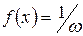 ,
, 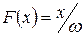 ,
, 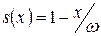 ,
, 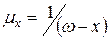 .
.
Сравнение графиков этих функций с реальными графиками функции выживания 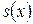 , функции смертей
, функции смертей 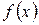 , интенсивности смертности
, интенсивности смертности 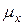 показывает, что закон де Муавра является не очень хорошим приближением. Например, первая формула означает, что кривая смертей
показывает, что закон де Муавра является не очень хорошим приближением. Например, первая формула означает, что кривая смертей 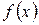 является горизонтальной линией, в то время как эмпирические данные указывают на пик в районе 80 лет.
является горизонтальной линией, в то время как эмпирические данные указывают на пик в районе 80 лет.
В модели, которую предложил в 1825г. Гомпертц, интенсивность смертности 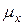 приближается показательной функцией вида
приближается показательной функцией вида 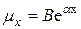 , где
, где 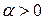 и
и 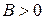 – некоторые параметры. Соответствующая функция выживания имеет вид
– некоторые параметры. Соответствующая функция выживания имеет вид
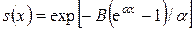 ,
,
а кривая смертей 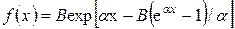 .
.
Мэйкхам в 1860 г. обобщил предыдущую модель, приблизив интенсивность смертности 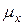 функцией вида
функцией вида 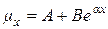 . Постоянное слагаемое
. Постоянное слагаемое 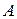 позволяет учесть риски для жизни, связанные с несчастными случаями (которые мало зависят от возраста), в то время как слагаемое
позволяет учесть риски для жизни, связанные с несчастными случаями (которые мало зависят от возраста), в то время как слагаемое 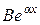 учитывает влияние возраста на смертность. В этой модели
учитывает влияние возраста на смертность. В этой модели
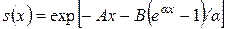 ,
,
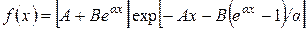 .
.
Второй закон Мэйкхама, введенный в 1889 году, приближает интенсивность смертности 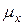 функцией вида
функцией вида 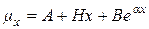 . В этой модели
. В этой модели
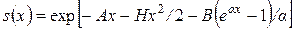 ,
,
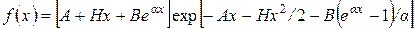 .
.
Вейбулл в 1939 году предложил приближать интенсивность смертности 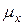 более простой степенной функцией вида
более простой степенной функцией вида 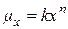 . В этой модели
. В этой модели
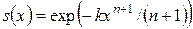 ,
, 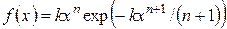 .
.
В модели Эрланга интенсивность смертности 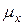 приближается функцией вида
приближается функцией вида 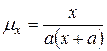 . В этой модели
. В этой модели
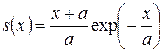 ,
, 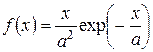 .
.
