Феноменологический подход
Микронаправление
В основе этого подхода лежит знание структуры элементов изучаемой системы, например, о молекулах, об атомах или даже о более мелких частицах. Используя законы физики, в том числе и механики, находятся общие законы поведения макросистем. В этом подходе используются модели , упрощающие применение общих законов природы.
В рамках этого направления существуют различные методы изучения:
· Динамический (механический) метод
Используются механические законы в рамках некоторых простых моделей и конкретные параметры (координаты, скорости, импульсы, энергия и т.д.). Затем устанавливается связь найденных параметров с параметрами состояния ТДС.
· Статистический метод
Этот метод НЕ ИСПОЛЬЗУЕТ конкретных моделей и значений механических параметров, в этом случае исследователя интересует распределения параметров. Поскольку если есть функция распределения некоего параметра (например, скорости), то можно вычислить среднее значение этого параметра и связать с параметрами состояния ТДС.
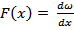 где ω– вероятность, то можно найти среднее значение этого параметра:
где ω– вероятность, то можно найти среднее значение этого параметра:
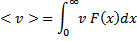
Таким образом, каждый параметр, характеризующий состояние системы, можно усреднить: 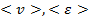 … (
… ( 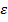 - энергия системы)
- энергия системы)
К плюсам этого метода можно отнести:
- можно применять любые законы, не только общие (в том числе и квантовые)
- этот метод позволяет предсказать, как будут протекать процессы в заданной системе с определенной вероятностью
Феноменологический подход
В основе этого подхода лежит эксперимент и использование макропараметров. Например для газа– давления (p), объема (V), температуры (T), массы (m), количества вещества … Затем экспериментально находятся взаимосвязи между этими макропараметрами, при этом не используется никаких моделей. При помощи такого подхода был выведен законы идеального газа закон Менделеева - Клапейрона:
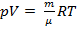 , где
, где 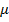 – молярная масса,
– молярная масса, 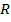 – универсальная газовая постоянная.
– универсальная газовая постоянная.
При любом анализе термодинамической системы необходимо знать:
Основные положения молекулярно-кинетической теории:
1. Все вещества состоят из атомов и молекул;
2. Эти атомы и молекулы находятся в непрерывном хаотическом движении, которое не прекращается ни при каких условиях
3. Атомы и молекулы взаимодействуют между собой с силами притяжения и отталкивания.
Помимо этих основных положений, для изучения статистической физики также пригодятся:
Закон сохранения и превращения энергии: 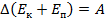 Второй закон Ньютона:
Второй закон Ньютона: 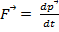
Закон сохранения импульса: 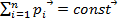
Теперь более подробно остановимся на основных положениях молекулярно-кинетической теории. Первое положение, в общем
очевидно.
Молекулярно-тепловое движение
Что касается второго положения, то тут необходимо заметить, что тепловое движение и хаотичное движения по своей сути не равносильны. Поскольку элементы системы могут обмениваться энергией (это интуитивно понятно), то энергию хаотичного движения логично представить в виде следующей формулы: 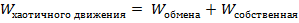 , причем вторая часть
, причем вторая часть 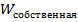 слагаемого не подлежит обмену (следовательно,
слагаемого не подлежит обмену (следовательно, 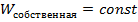 ), а первая может быть взята (отдана )в систему. Как раз первая составляющая -
), а первая может быть взята (отдана )в систему. Как раз первая составляющая - 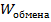 – и есть тепловая энергия.
– и есть тепловая энергия.
Рассмотрим отдельно кинетическую энергию системы 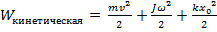 , причем
, причем 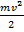 – составляющая, отвечающая за поступательное движение,
– составляющая, отвечающая за поступательное движение, 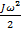 – за вращательное движение,
– за вращательное движение, 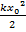 – за колебательное. Даже из этого выражения можно выразить целых 9 независимых параметров, характеризующих
– за колебательное. Даже из этого выражения можно выразить целых 9 независимых параметров, характеризующих 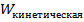 :
:
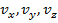
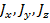
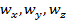
Для данной системы эти независимые параметры можно считать координатами. Если обобщить данный факт, то можно ввести следующее: число независимых переменных, определяющих состояние системы, – есть число степеней свободы. Таким образом, если 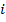 – число степеней свободы для одного элемента, то
– число степеней свободы для одного элемента, то 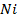 – число степеней свободы всей системы (в ней
– число степеней свободы всей системы (в ней 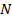 элементов). Таким образом, мы получаем фазовое пространство, в котором каждая точка характеризуется большим чистом координат (подробнее о фазовом пространстве будет позднее). Главное, что мы получаем крайне сложную задачу по поиску закономерностей в термодинамической системе.
элементов). Таким образом, мы получаем фазовое пространство, в котором каждая точка характеризуется большим чистом координат (подробнее о фазовом пространстве будет позднее). Главное, что мы получаем крайне сложную задачу по поиску закономерностей в термодинамической системе.
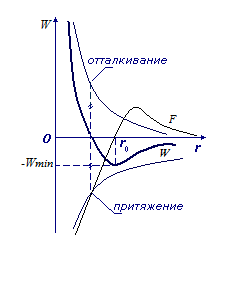 Перейдем теперь к третьему пункту в основных положениях МКТ – к силам. Формула Леннарда-Джонсона описывает энергию взаимодействия между молекулами:
Перейдем теперь к третьему пункту в основных положениях МКТ – к силам. Формула Леннарда-Джонсона описывает энергию взаимодействия между молекулами:
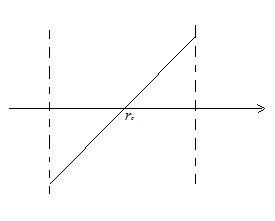
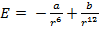 , где a и b – некоторые константы. Отсюда можно найти силу взаимодействия между молекулами:
, где a и b – некоторые константы. Отсюда можно найти силу взаимодействия между молекулами: 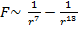 , где
, где 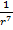 – как раз составляющая, отвечающая за силы притяжения, а
– как раз составляющая, отвечающая за силы притяжения, а 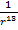 – за силы отталкивания.
– за силы отталкивания.
Рассмотрим расстояния 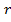 , близкие к
, близкие к 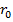 . В окрестности этой точки график функции
. В окрестности этой точки график функции 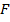 близок к отрезку прямой, проходящей через
близок к отрезку прямой, проходящей через 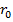 . Таким образом:
. Таким образом:
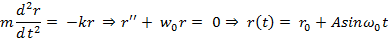
В результате получаем, что характер движения около 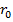 – колебательный. Это характерно для твердых тел. В жидкости характер движения молекул – колебательный с перескоком в новое положение. В газе
– колебательный. Это характерно для твердых тел. В жидкости характер движения молекул – колебательный с перескоком в новое положение. В газе 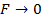 и, следовательно, в газе молекула движется поступательно от одного соударения до другого.
и, следовательно, в газе молекула движется поступательно от одного соударения до другого.
Равновесное состояние ТДС. Температура.
ТДС находится в равновесном состоянии, если при неизменных внешних условиях она может находиться в этом состоянии сколь угодно долго.
Если один из параметров, характеризующих систему ( 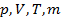 ) постоянен при неизменных внешних условиях, то система равновесна по этому параметру (речь как раз идет об изопроцессах: при постоянной температуре – изотерма, при постоянном давлении – изобара и т.п.)
) постоянен при неизменных внешних условиях, то система равновесна по этому параметру (речь как раз идет об изопроцессах: при постоянной температуре – изотерма, при постоянном давлении – изобара и т.п.)
Если все макропараметры неизменны и одинаковы во всех точках системы, то замкнутая система находится в равновесном состоянии. Пусть имеется две термодинамические системы, причем они взаимодействуют только через линию соприкосновения. Системы не могут реагировать химически, не могут расширяться одна за счёт другой, не могут обмениваться массой и энергией движения, как единого целого. Т. е, можно обмениваться только энергией теплового движения:  .
.
Статистическая физика утверждает, что равновесное состояние по  наступит, когда:
наступит, когда: 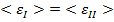 , где
, где 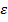 – средняя энергия одной молекулы.
– средняя энергия одной молекулы.
Например, для идеального газа (математическая модель газа, в которой предполагается, что потенциальной энергией взаимодействия молекул можно пренебречь по сравнению с их кинетической энергией, между молекулами не действуют силы притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями) будет верно: 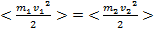
Таким образом, равновесный параметр - 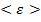 будет равен
будет равен 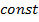 .
.
Но средняя энергия не очень удобный параметр для практических измерений и сложно связан с другими параметрами состояния ТДС. Было предложено ввести некоторый параметр, пропорциональный средней энергии системы в равновесном состоянии: 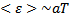 Удобным коэффициентом оказался a=
Удобным коэффициентом оказался a= 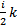 . Тогда
. Тогда 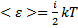 , где Т- абсолютная температура.
, где Т- абсолютная температура.
Замечание: 1. Для установления состояния равновесия необходимо некоторое время. Если две термодинамические системы обмениваются энергией, то время выравнивание температур (а следовательно, и средних энергий молекул) называется временем релаксации. Например, необходимо некоторое время, чтобы получить точные данные при помощи термометра.
2. Принцип температуры является содержанием нулевого начала термодинамики: Нулевое начало термодинамики (общее начало термодинамики) — физический принцип, утверждающий, что вне зависимости от начального состояния изолированной системы в конце концов в ней установится термодинамическое равновесие, а также что все части системы при достижении термодинамического равновесия будут иметь одинаковую температуру.
Раздел 2. Динамическая теория идеального газа.
2.1 Давление и среднее энергия молекул газа. Основное уравнение МКТ идеального газа. Изопроцессы.
Рассмотрим моноскоростной пучок молекул, ударяющийся об стенку (скорость молекул перпендикулярна поверхности стенки). Молекулы долетают до стенки площади 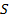 и абсолютно упруго отскакивают от нее.
и абсолютно упруго отскакивают от нее.
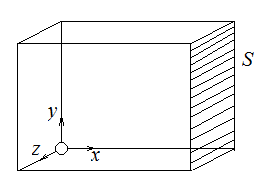
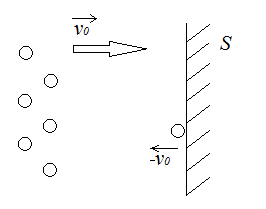
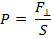 Найдем давление
Найдем давление 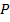 , оказываемое этим пучком на стенку. Разность импульсов для каждой молекулы равна:
, оказываемое этим пучком на стенку. Разность импульсов для каждой молекулы равна:
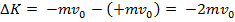 ⇒ стенка получает импульс
⇒ стенка получает импульс 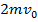 от одной молекулы. Известно, что
от одной молекулы. Известно, что 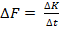 . За время
. За время 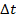 будет пройден путь
будет пройден путь 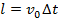 . Таким образом, все молекулы в объеме
. Таким образом, все молекулы в объеме 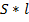 успеют ударить стенку. Итак,
успеют ударить стенку. Итак, 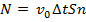 , где
, где 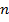 – концентрация. Отсюда
– концентрация. Отсюда 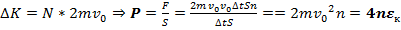
Но в идеальном газе все молекулы движутся хаотично и непрерывно, следовательно, по каждому из 6 возможных направлений единовременно движется 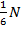 молекул.
молекул.
Тогда:
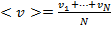
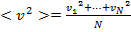
Тогда 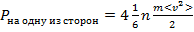 . С учетом того, что
. С учетом того, что 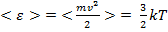 , получаем:
, получаем:
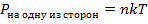 , где
, где 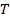 – макропараметр, температура.
– макропараметр, температура.
Правильность полученного результата можно проверить по закону Менделеева - Клапейрона, который является чисто экспериментальным, и, следовательно, независимым от проделанных выше умозаключений:
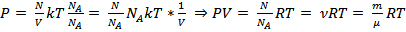 , что верно.
, что верно.
Мы получили основное уравнение молекулярно-кинетической теории: 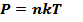 Полученное уравнение позволяет получить и другие уравнения состояния идеального газа. Например,можно выделить следующие изопроцессы:
Полученное уравнение позволяет получить и другие уравнения состояния идеального газа. Например,можно выделить следующие изопроцессы:
1. Изотермический: 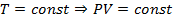 (разумеется, если также соблюдены следующие условия:
(разумеется, если также соблюдены следующие условия: 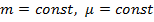 . 2. Изобарический:
. 2. Изобарический: 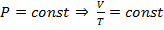 (при
(при 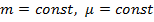 ).
).
3. Изохорический: V=Const→ 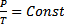 (при
(при 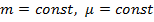 ).
).
Замечание: можно проверить единицы измерения. Энергия и работа измеряются в джоулях. 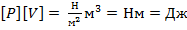 – итак, что в основном уравнении МКТ в левой части стоит нечто, измеряющееся в джоулях. Очевидно, что это – некоторая энергия, причем зависит она только от макропараметров системы. С другой стороны,
– итак, что в основном уравнении МКТ в левой части стоит нечто, измеряющееся в джоулях. Очевидно, что это – некоторая энергия, причем зависит она только от макропараметров системы. С другой стороны, 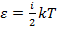 – энергия, которая, которая зависит от микропараметров:
– энергия, которая, которая зависит от микропараметров: 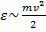 , то есть энергия – это функция микропараметров. Отсюда ясно видна связь между микро- и макропараметрами.
, то есть энергия – это функция микропараметров. Отсюда ясно видна связь между микро- и макропараметрами.
 2.2 Столкновения молекул. Средняя длина свободного пробега молекул. Явления переноса в газах: диффузия, внутренне трение, теплопроводность.
2.2 Столкновения молекул. Средняя длина свободного пробега молекул. Явления переноса в газах: диффузия, внутренне трение, теплопроводность.
| α |
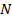 молекул. Пусть
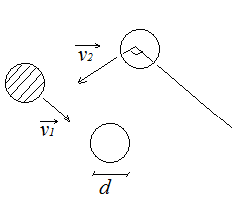
молекул. Пусть 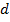 – диаметр одной молекулы. Предположим, что все молекулы покоятся, а одна, за которой мы наблюдаем, движется с относительной скоростью. Введем относительная скорость:
– диаметр одной молекулы. Предположим, что все молекулы покоятся, а одна, за которой мы наблюдаем, движется с относительной скоростью. Введем относительная скорость: 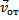 =
= 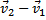
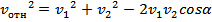
Но поскольку молекул в настоящей системе слишком много, то в реальности исследователь имеет дело лишь со средней скоростью:
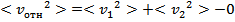
(0 возникает, поскольку угол 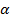 лежит от
лежит от 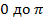 , следовательно, среднее значение косинуса равно 0). Тогда
, следовательно, среднее значение косинуса равно 0). Тогда
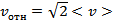 - тепловая относительная скорость. Теперь пусть все молекулы, кроме одной, покоятся.
- тепловая относительная скорость. Теперь пусть все молекулы, кроме одной, покоятся.
Тогда за одну секунду молекула столкнется со всеми молекулами в объеме 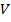 :
: 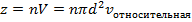
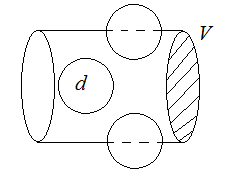 Таким образом,
Таким образом, 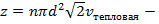 число столкновений за одну секунду, причем
число столкновений за одну секунду, причем 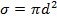 – это сечение столкновений (это понятие ввел академик Семёнов)
– это сечение столкновений (это понятие ввел академик Семёнов)
Если в качестве примера газовой смеси
взять воздух, то для него:
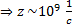 |
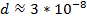
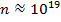
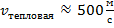
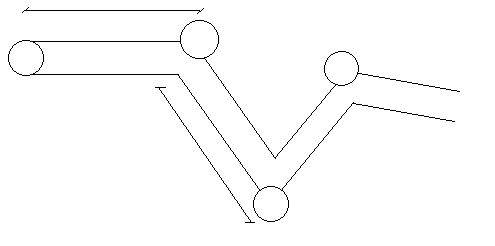 Найдем среднюю длину свободного пробега
Найдем среднюю длину свободного пробега 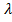 – то есть
– то есть
длину среднего пути, проходимого молекулой без столкновений.
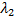 |
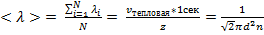 Отсюда получаем:
Отсюда получаем: 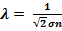 –микропараметр. Осталось выяснить, как этот микропараметр связан с макропараметрами, и какими именно. Среднюю длину свободного пробега можно также очевидно выразить через макропараметры:
–микропараметр. Осталось выяснить, как этот микропараметр связан с макропараметрами, и какими именно. Среднюю длину свободного пробега можно также очевидно выразить через макропараметры: 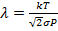 , где
, где 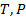 – макропараметры.
– макропараметры. Рассмотрим зависимость длины свободного пробега от температуры и давления.
· Зафиксируем 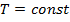 . Если увеличить
. Если увеличить 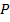 (например, увеличить количество частиц, то есть увеличить концентрацию), то
(например, увеличить количество частиц, то есть увеличить концентрацию), то 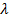 , очевидно, уменьшится.
, очевидно, уменьшится.
· Теперь нагреваем замкнутый фиксированный объем 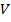 .
.
То есть  . Чисто теоретически
. Чисто теоретически 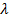 меняться не должно. Но практически это не так. Надо обратить внимание на диаметр молекулы
меняться не должно. Но практически это не так. Надо обратить внимание на диаметр молекулы 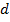 . Он является динамическим.
. Он является динамическим.
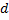 |
Эффективный диаметр молекулы – это наименьшее расстояние, на которое могут сблизиться центры молекул. Но при увеличении температуры в системе увеличивается тепловая скорость молекул, следовательно, эффективный диаметр уменьшается, и, следовательно, 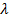 увеличивается.
увеличивается.
λ
Т
Явление переноса в газах. Диффузия.
Диффузия – это явление распространения молекул примеси в газовой среде (в общем случае это может быть и жидкость, и твердые тела) от точки ввода. При этом для воздуха верно:

Исследуем распространение молекул примеси вдоль одной оси (затем продолжим для всех направлений)
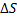 |
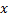 |
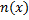 |
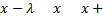 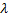 |
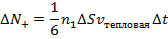
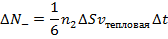
При этом первое выражение используется для подсчета числа молекул, движущихся в положительном направлении оси ox, второе – в отрицательном. Таким образом, можно подсчитать число молекул, проходящее через площадку 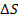 в единицу времени:
в единицу времени:
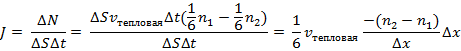
Отсюда получаем следующую формулу: 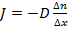 , где
, где 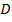 – это коэффициент диффузии, а
– это коэффициент диффузии, а 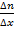 – это так называемый градиент концентрации. Поскольку
– это так называемый градиент концентрации. Поскольку 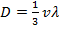 (это следует из того, что
(это следует из того, что 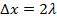 ), то из очевидной связи микропараметров
), то из очевидной связи микропараметров 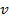 и
и 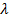 от макропараметров:
от макропараметров: 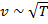 и
и 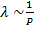 следует зависимость коэффициента диффузии от макропараметров (от температуры и давления): при увеличении температуры коэффициент диффузии увеличивается. С интуитивной точки зрения это понятно: запах распространяется быстрее при более высокой температуре. Аналогично – при уменьшении давления.
следует зависимость коэффициента диффузии от макропараметров (от температуры и давления): при увеличении температуры коэффициент диффузии увеличивается. С интуитивной точки зрения это понятно: запах распространяется быстрее при более высокой температуре. Аналогично – при уменьшении давления.
Внутреннее трение газа (вязкость)
Проведем следующий эксперимент: возьмем два цилиндра различного диаметра, поместим один внутрь другого, внешний цилиндр начнем вращать с некоторой скоростью 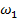 , внутренний цилиндр покоится. Однако, через
, внутренний цилиндр покоится. Однако, через
некоторое время внутренний цилиндр также придет в движение и начнет вращаться, несмотря на то, что видимого приложения силы к нему нет. Отсюда вывод, что на внутренний цилиндр каким-то образом влияет среда между двумя цилиндрами, а именно – воздух.
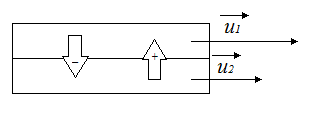
У каждого слоя молекул в этой воздушной прослойке имеется
своя скорость: у слоя, вплотную примыкающего к внешнему цилиндру, будет скорость 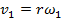 , у слоя, примыкающего к внутреннему цилиндру -
, у слоя, примыкающего к внутреннему цилиндру - 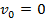 .
.
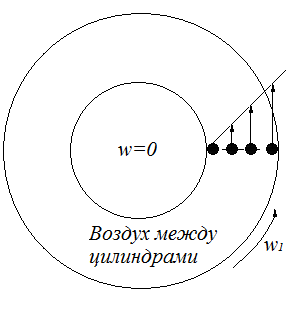 Пусть имеется два соседних слоя молекул, у первого слоя скорость
Пусть имеется два соседних слоя молекул, у первого слоя скорость 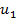 , а у второго -
, а у второго - 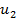 . Молекулы вследствие теплового движения перемещаются между слоями. Обозначим направление от второго слоя к первому как положительное, обратно – отрицательное. Поскольку мы рассматриваем идеальный газ, то имеют место только силы соударения молекул, никаким иным способом они не взаимодействуют. По второму закону Ньютона:
. Молекулы вследствие теплового движения перемещаются между слоями. Обозначим направление от второго слоя к первому как положительное, обратно – отрицательное. Поскольку мы рассматриваем идеальный газ, то имеют место только силы соударения молекул, никаким иным способом они не взаимодействуют. По второму закону Ньютона: 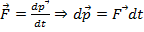
 Таким образом, единственный способ в данной ситуации привести в движение более медленные слои воздуха – это передать им некоторый импульс. Покажем, что изменение импульса действительно имеет место быть.
Таким образом, единственный способ в данной ситуации привести в движение более медленные слои воздуха – это передать им некоторый импульс. Покажем, что изменение импульса действительно имеет место быть.
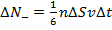
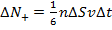
+Таким образом, у потоков, несмотря на одинаковое количество переходящих друг в друга частиц, разное количество направленного движения: 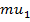 и и 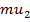 . Тогда можно найти изменение импульса за некоторое время: . Тогда можно найти изменение импульса за некоторое время: |
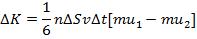
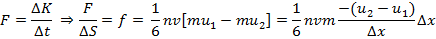
где 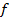 – сила внутреннего трения. Поскольку
– сила внутреннего трения. Поскольку 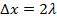 , получаем:
, получаем: 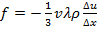 , где
, где 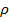 – плотность. Или:
– плотность. Или:
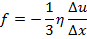 где
где 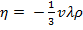 – коэффициент внутреннего трения,
– коэффициент внутреннего трения, 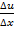 – градиент скорости направленного движения слоев.
– градиент скорости направленного движения слоев.
Таким образом, сила внутреннего трения прямо пропорциональна градиенту скорости направленного движения слоев, или, иными словами, сила внутреннего трения прямо пропорциональна переносимому импульсу направленного движения из слоя в слой.
Параметр 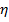 определяет физические свойства газа и называется вязкостью. Очевидно, что
определяет физические свойства газа и называется вязкостью. Очевидно, что 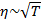
Теплопроводность
Из закона Менделеева - Клапейрона путем нахождения дифференциала от обеих частей равенства следует: 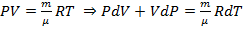 , где
, где 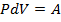 – некоторая работа, а
– некоторая работа, а 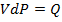 – некоторое количество тепла (та самая часть энергии хаотического движения, которой могут обмениваться атомы и молекулы и, следовательно, целые системы).
– некоторое количество тепла (та самая часть энергии хаотического движения, которой могут обмениваться атомы и молекулы и, следовательно, целые системы).
Существует три основных классических способа передачи тепла от тела к телу:
· Теплопроводность (при непосредственном контакте)
· Конвекция (перемешивание слоев жидкости или газа)
· Излучение
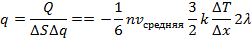 |
 L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEADv9by8AA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERP32vCMBB+F/wfwgm+aeooY1SjiDDY02Ct6/PRnE2x uZQk09q/3gwGe7uP7+ftDqPtxY186Bwr2KwzEMSN0x23Cs7V++oNRIjIGnvHpOBBAQ77+WyHhXZ3 /qJbGVuRQjgUqMDEOBRShsaQxbB2A3HiLs5bjAn6VmqP9xRue/mSZa/SYsepweBAJ0PNtfyxCurW TvX3ZvBG2z7nz+lRnV2n1HIxHrcgIo3xX/zn/tBpfpbD7zPpArl/AgAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEADv9by8AAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA== " stroked="f" strokeweight=".5pt">
L t1UKDXHTtVBSKC5JzEtJzMnPS7VVqkwtVrK34+UCAAAA//8DAFBLAwQUAAYACAAAACEADv9by8AA AADcAAAADwAAAGRycy9kb3ducmV2LnhtbERP32vCMBB+F/wfwgm+aeooY1SjiDDY02Ct6/PRnE2x uZQk09q/3gwGe7uP7+ftDqPtxY186Bwr2KwzEMSN0x23Cs7V++oNRIjIGnvHpOBBAQ77+WyHhXZ3 /qJbGVuRQjgUqMDEOBRShsaQxbB2A3HiLs5bjAn6VmqP9xRue/mSZa/SYsepweBAJ0PNtfyxCurW TvX3ZvBG2z7nz+lRnV2n1HIxHrcgIo3xX/zn/tBpfpbD7zPpArl/AgAA//8DAFBLAQItABQABgAI AAAAIQDw94q7/QAAAOIBAAATAAAAAAAAAAAAAAAAAAAAAABbQ29udGVudF9UeXBlc10ueG1sUEsB Ai0AFAAGAAgAAAAhADHdX2HSAAAAjwEAAAsAAAAAAAAAAAAAAAAALgEAAF9yZWxzLy5yZWxzUEsB Ai0AFAAGAAgAAAAhADMvBZ5BAAAAOQAAABAAAAAAAAAAAAAAAAAAKQIAAGRycy9zaGFwZXhtbC54 bWxQSwECLQAUAAYACAAAACEADv9by8AAAADcAAAADwAAAAAAAAAAAAAAAACYAgAAZHJzL2Rvd25y ZXYueG1sUEsFBgAAAAAEAAQA9QAAAIUDAAAAAA== " stroked="f" strokeweight=".5pt">  |
 |
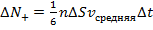
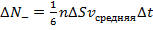
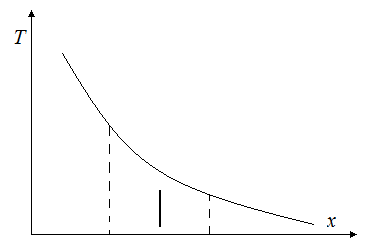
Таким образом: 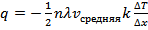 или
или 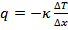 , где
, где 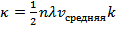 – коэффициент теплопроводности.
– коэффициент теплопроводности.
Раздел 3. Основы статистического описания термодинамических систем
3.1 Основные понятия. Микро- и макропараметры состояния. Равновесные состояния системы. Понятие фазового пространства и его свойства.
Введем некоторые основные понятия (некоторые из них могут повторяться с тем, что уже было раньше, но большей частью это либо новые, либо углубленные понятия).
Термодинамическая система – это любая система (то есть любое тело), состоящая из множества частиц (то есть макротело).
Существуют параметры, характеризующие эту термодинамическую систему:
- микропараметры (величины, которые характеризующие состояние элементов системы)
- макропараметры (характеризуют состояние всей системы или ее частей)
К примерам первых можно отнести скорость одной молекулы, а вторых – массу системы, давление, температура.
Для описания замкнутости или не замкнутости используются так называемые внешние и внутренние параметры.
Цель и применение статистического метода:
В случае статистического метода не используются параметры отдельных частиц, ищутся общие закономерности для всех частиц сразу, микропараметры не нужны сами по себе, их используют только для нахождения распределений микропараметров по их значениям. Целью метода является нахождение общих закономерностей при помощи знаний законов статистической физики.
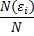 |
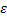 |
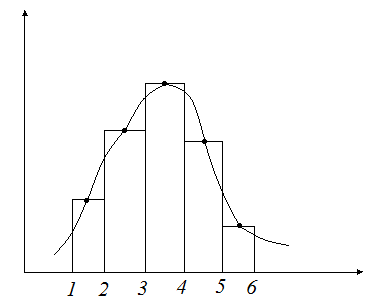
Пусть мы можем измерить в термодинамической системе относительное число частиц с определенной энергией (энергией, входящий в определенный интервал) – получится гистограмма определенного вида (смотри рисунок). Эта операция вычисления относительного числа частиц с определенной энергией повторяется много раз. Получаемая гистограмма будет колебаться около одного (наивероятнейшего) положения некоторой кривой. Тогда будет возможно найти средние значения 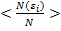 , для
, для
i-того интервала энергий, которые будут устойчивыми. Таким образом, мы будем находить некоторое соответствие относительного числа частиц определённому интервалу энергий. Это соответствие в виде графика, аналитического закона или в другой форме и есть распределение частиц по энергиям.
Среди всевозможных распределений существует такое распределение, которое реализуется наибольшим числом микросостояний элементов системы. Это распределение и является наиболее вероятным, равновесным.
Равновесное состояние (в статистическом смысле) – это такое состояние системы, которое характеризуется наибольшим числом микросостояний. В таком случае говорят, что система находится в равновесии.
Например, 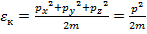 . Если выбрать определенный интервал энергий, то найдутся разные числа
. Если выбрать определенный интервал энергий, то найдутся разные числа
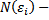 разные частицы (i) , с разными значениями составляющих импульсов, дающие одинаковое значение энергии.
разные частицы (i) , с разными значениями составляющих импульсов, дающие одинаковое значение энергии.
Более того, само значение импульса или энергии, если абстрагироваться от обычных систем координат, можно воспринимать как координату. Строго говоря, координатами (то есть состояниями) в системе может являться все, что угодно. Так возникает понятие фазового пространства.
Фазовое пространство – это пространство, координатами которого являются микропараметры термодинамической системы.
Если какая-то величина 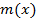 может принимать какие-то значения от
может принимать какие-то значения от 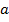 до
до 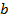 , то тогда можно представить одномерное фазовое пространство. Причем точные знания параметров не нужны, достаточно просто разбить ось на небольшие отрезки
, то тогда можно представить одномерное фазовое пространство. Причем точные знания параметров не нужны, достаточно просто разбить ось на небольшие отрезки 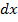 – достаточно малые значения, причем именно
– достаточно малые значения, причем именно 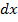 – будет являться элементом фазового пространства, иначе говоря – элементом объема фазового пространства.
– будет являться элементом фазового пространства, иначе говоря – элементом объема фазового пространства.
Также можно представить двумерное фазовое пространство 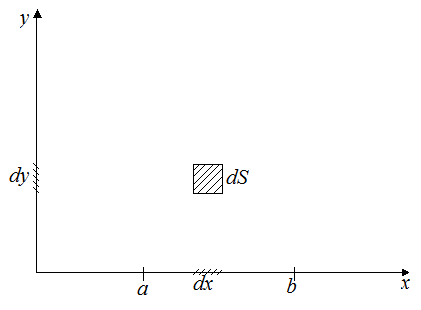 . В таком случае у нас имеется величина
. В таком случае у нас имеется величина 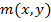 и объемом фазового пространства будет являться
и объемом фазового пространства будет являться 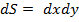
Аналогично – и для пространств с большей размерностью. Для объема фазового пространства характерно перемножение объемов фазовых пространств меньших размерностей.
Это свойство мультиплексности: объемы умножаются.
Перейдем теперь к энергетическому состоянию. В этом случае для каждого элемента системы будет 6 независимых координат:
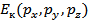
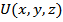 Образуемое этим шестью координатами фазовое пространство называется
Образуемое этим шестью координатами фазовое пространство называется
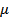 – пространством. Элементом объема такого пространства будет являться выражение вида:
– пространством. Элементом объема такого пространства будет являться выражение вида:
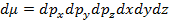
Причем это пространство можно разбить на два подпространства, 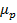 и
и 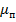 , объем которых будет соответственно:
, объем которых будет соответственно: 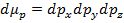 и
и 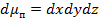 .
.
В конечном итоге мы всегда можем подобрать наиболее удобное для решения определенной задачи фазовое пространство и разбить его именно на те подпространства, которые будут наиболее легки в понимании и расчетах.
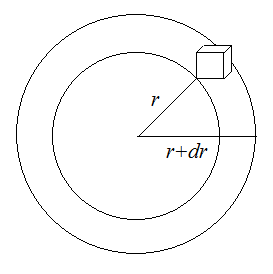 Например, рассмотрим некоторый шар, радиус которого будет составлять R. Если нам захочется вести некоторые вычисления в самом примитивном фазовом пространстве – геометрическом, то в качестве объема фазового пространства придется взять элементарный «кубик», который будет крайне неудобен при описании величин являющихся функцией радиуса (r). Но если в качестве элемента объема фазового пространства взять элементарный объем шарового слоя толщиной
Например, рассмотрим некоторый шар, радиус которого будет составлять R. Если нам захочется вести некоторые вычисления в самом примитивном фазовом пространстве – геометрическом, то в качестве объема фазового пространства придется взять элементарный «кубик», который будет крайне неудобен при описании величин являющихся функцией радиуса (r). Но если в качестве элемента объема фазового пространства взять элементарный объем шарового слоя толщиной 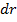 :
: 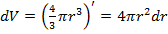 , то есть
, то есть 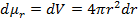 , что намного удобнее первоначального способа. Таким образом, всегда можно определить наиболее удобный элемент фазового пространства
, что намного удобнее первоначального способа. Таким образом, всегда можно определить наиболее удобный элемент фазового пространства
3.2 Элементы теории вероятностей. Случайные величины и их описание. Функция распределения. Средние значения, математическое ожидание, дисперсия и флуктуация. Биномиальное распределение. Распределение в системах с большим количеством элементов. Распределения Пуассона и Гаусса.
Случайное событие – это событие, которое может произойти, а может и не произойти.
Регулярное (достоверное) событие – событие, которое происходит всегда.
Невозможное событие – событие, которое никогда не происходит.
Случайная величина – это количественная величина, характеризующая некоторое случайное событие. Для того, чтобы задать случайную величину, недостаточно просто задать ее значения, необходимо знать вероятность того, что она примет это значение.
Вероятность определяется как величина 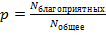 при достаточно больших
при достаточно больших 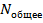 .
.
Свойства вероятности:
1. 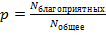
2. Сумма вероятностей: s New Roman" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="24"/><w:sz-cs w:val="24"/></w:rPr><m:t>+p(C)</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></wx:sect></w:body></w:wordDocument>"> 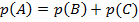 – вероятность того, что произойдет событие
– вероятность того, что произойдет событие 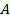 , заключающееся в том, что произойдет либо
, заключающееся в том, что произойдет либо 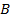 , либо
, либо 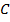 (речь идет о несовместных событиях).
(речь идет о несовместных событиях).
3. Произведение вероятностей: 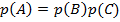 – вероятность того, что произойдет событие
– вероятность того, что произойдет событие 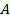 , заключающееся в том, что произойдет и
, заключающееся в том, что произойдет и 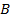 , и
, и 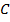 (события совместимы).
(события совместимы).
4. Условие нормировки: если случайных событий 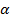 штук и только этим исчерпываются все значения случайной величины:
штук и только этим исчерпываются все значения случайной величины:  , которые случайная величина принимает с вероятностями
, которые случайная величина принимает с вероятностями 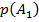 , … ,
, … , 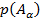 , то тогда выполняется условие нормировки:
, то тогда выполняется условие нормировки: 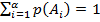
Следствие: если событие 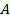 реализуется с вероятностью
реализуется с вероятностью 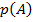 , то событие
, то событие 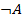 (обратное А) реализуется с вероятностью
(обратное А) реализуется с вероятностью 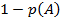 .
.
