Цифрами на графике обозначены результаты пловцов (секунды), соответствующие значениям скорости плавания (м/с) по оси ординат
Практически это сводится к отысканию наиболее подходящего в каждом конкретном случае вида математической функции, отражающей динамику наблюдаемого процесса. В нашем примере такой функцией может быть линейная или степенная (последняя дает более корректные результаты). Плавно продолжая линию за пределы анализируемого ряда данных (см. пунктир на графике) или рассчитав и подставив в уравнение функции соответствующие числовые значения, мы получаем возможность судить о вероятном результате будущего олимпийского чемпиона.
Следует отметить, что при длительной экстраполяции (на 6-8 лет вперед) часто наблюдается расхождение прогнозируемых результатов с реальными. Это обусловлено несколькими факторами:
1) появлением принципиально новых тренировочных программ, позволяющих существенно повысить уровень специальной подготовленности спортсмена;
2) появлением выдающихся личностей – спортивных талантов, расширяющих представление о человеческих возможностях;
3) условиями проведения крупнейших международных состязаний, которые могут существенно отличаться от обычных.
Выбор типа эктраполяционной функции зависит от задач прогнозирования, спортивной дисциплины. В каждом конкретном случае могут быть подобраны наиболее эффективные математические формулы. Практика показала, что в циклических видах спорта для прогнозирования олимпийских и мировых достижений могут применяться следующие элементарные функции:
Линейная: y=a0+a1x (1)
Степенная: y=axb (2)
Экспонента: y=ae-bx (3)
Квадратичная: y=a0+a1x+a2x2 (4)
где y – прогнозируемый результат; x - время; a, a0, a1, a2 – расчетные коэффициенты уравнения; b – расчетный показатель степени; e – основание логарифмов.
Процедура прогнозирования с помощью математических методов всегда дополняется содержательным анализом исходных и получаемых результатов, внесением в прогноз необходимых корректив путем экспертных суждений – мнений опытных специалистов в данном виде спорта.
В работе со спортивным резервом практическую значимость для тренера приобретает прогноз многолетней динамики спортивного результата. Как правило, на кривой, отражающей многолетнюю возрастную динамику, различают два участка:
1. соответствующий периоду базовой подготовки юных спортсменов, от начала регулярных тренировочных занятий (9-10 лет у девочек, 10-11 лет у мальчиков) до первых больших успехов (14-15 лет у девушек, 16-17 лет у юношей);
2. относящийся к периоду оптимальных возможностей демонстрации максимально высоких результатов и совпадающий с этапом высшего спортивного мастерства.
Для математического описания индивидуальной многолетней динамики спортивных результатов оправдано применение экспоненциального уравнения вида:
y = K – ae-bx
где y – результат в отдельно взятом году; K – предельный результат данного спортсмена; a – прирост результатов за анализируемый период; b – константа скорости прироста результатов; e – основание логарифмов; x – количество лет от начала тренировки.
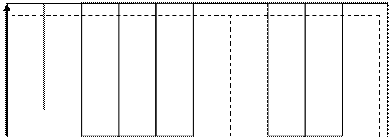
Экспоненциальная зависимость хорошо соответствует реальности: наиболее высокие темпы прироста результатов наблюдаются на этапе базовой подготовки, совпадающем с пубертатным ускорением роста и формирования организма; на этапе высшего спортивного мастерства спортивные достижения могут долгое время удерживаться примерно на одном уровне. На рисунке 8 для примера показана экспонента, отражающая возрастную динамику результатов спортсменки (мастер спорта в плавании вольным стилем) за 9 лет занятий.
 | |||
 | |||






 В С
В С
 | |||||
 | |||||
 |

 А
А
 |
9 10 11 12 13 14 15 16 17 18
Возраст, лет
Рисунок 8. Возрастная динамика спортивных результатов на дистанции 100 метров вольным стилем (в пересчете на скорость плавания) спортсменки Х. за 9-ти летний период занятий и теоретическое отображение экспоненциальной кривой.
