Задания для самостоятельного решения

МЕТОД МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ

Это метод доказательства некоторого утверждения для любого натурального n, основанный на следующем принципе:

Если утверждение верно для n = 1 (базис индукции),

и из справедливости его для n = k (предположение индукции),

вытекает справедливость этого утверждения для n = k + 1 (индукционный шаг),

то оно верно для всех n.

Часто доказательство по индукции имеет форму «спуска»:

Если утверждение верно для n=1

и (при n>1) из справедливости его для всех k < n

следует справедливость для k = n,

то утверждение верно для всех n.

Замечание!

Иногда удобно начать индукцию не с n = 1, a c n = 0 или с некоторого n = n₀.

Принцип индукции эквивалентен аксиоме:

«В любом множестве натуральных чисел есть наименьшее»

ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ

ЗАДАЧА 1

Доказать, что 1² + 2² + 3² + …+ n² = 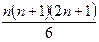для любого натурального n.

Доказательство:

1. Базис индукции

Проверим справедливость утверждения при n = 1.

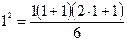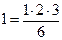, , 1 = 1 – верно.

2. Предположение индукции

Предположим, что утверждение верно при n = k, т.е. справедливо равенство

1² + 2² + 3² + …+ k² = .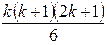

3. Индукционный шаг

Докажем, что утверждение верно и при n=k+1, т.е.

1² + 2² + 3² + …+ k² + (k + 1)² = .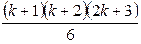

Действительно, 1² + 2² + 3² + …+ k² + (k + 1)² = 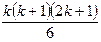+ (k + 1)² = =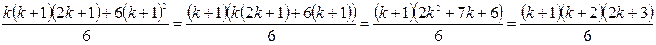

Таким образом, доказана справедливость утверждения

1² + 2² + 3² + …+ n² = 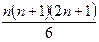для любого натурального n.

ЗАДАЧА 2

Доказать, что (3²ⁿ⁺¹ + 40n – 67) : 64 при любом натуральном n.

Доказательство:

1. Базис индукции

Проверим справедливость утверждения при n = 1.

(3^2×1+1 + 40×1 – 67) = 27 + 40 – 67 = 0,

0 : 64 – верно.

2. Предположение индукции

Предположим, что утверждение верно при n = k,

т.е. справедливо (3^2k+1 + 40k – 67) : 64

3. Индукционный шаг

Докажем, что утверждение верно и при n = k + 1, т.е. (3^2(k+1)+1 + 40(k + 1) – 67) : 64.

Действительно,

3^2(k+1)+1 + 40(k + 1) – 67 = 3^2k+3 + 40k – 27 = 9×(3^2k+1 + 40k – 67) – 320k +576 =

= 9×(3^2k+1 + 40k – 67) – 64×(5k – 9).

Так как каждое слагаемое делится на 64, то и вся сумма делится на 64.

Таким образом, доказана справедливость утверждения (3²ⁿ⁺¹ + 40n – 67) : 64

для любого натурального n.

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ

1. Докажите, что при каждом натуральном n число 13×(–50)ⁿ + 17×40ⁿ – 30 делится на 1989.

2. Докажите, что сумм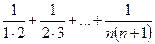а равна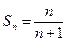

3. Докажите неравенство Бернулли: (1 + a)ⁿ > 1 + na, где a > –1, a ¹ 0, n – натуральное число, большее 1.

4. Докажите, что при любом натуральном n

1³ + 2³ + … + n³ = (1 + 2 + … + n)².

5. Докажите, что число (1 + 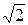)²⁰¹² представляется в виде а + b 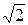, где а и b – взаимно простые числа.

6. Докажите, что при любом натуральном n справедливо равенство

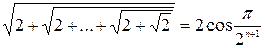
7. Докажите методом математической индукции:

а) 1×4 + 2×7 + 3×10 + …+ n(3n+1) = n(n+1)².

б) (n+1)×(n+2)×…×(n+n)=2ⁿ×1×3×5×…×(2n – 1).

в) .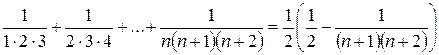

г) .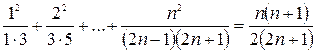

д) 2×1² + 3×2² + …+(n+1)n²= .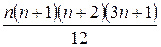

е)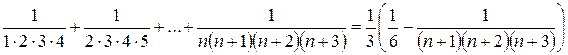

8. Последовательность {a_n} задана рекуррентным способом: а₁=1, а₂=1 и а_n+2=a_n+1+ 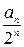для n ³ 1. Докажите, что a_n < 3 при всех n.

9. Числа а₁, а₂, …, a_n таковы, что 0 £ а₁ £ а₂ £ 2а₁, а₂ £ а₃ £ 2а₂, …, a_n–1 £ a_n £ 2a_n–1. Докажите, что в суммме S = ± a₁ ± a₂ ± … ± a_n можно так выбрать знаки, чтобы было 0 £ S £ a₁.

10. На плоскости дан набор из n векторов, длина каждого из которых не превосходит единицы. Докажите, что, заменив некоторые векторы из этого набора на противоположные, можно получить набор векторов, сумма которых имеет длину, не превосходящую .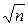

11. Последовательность а₁, а₂, а₃, … образована по следующему правилу:

а₁ = 1, а₂ = а₁ + 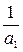, …, а_n = a_n–1 + .

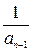Докажите, что а₁₀₀ > 14.