Приложение I. ПОГРЕШНОСТИ ПРЯМЫХ И КОСВЕННЫХ ИЗМЕРЕНИЙ
Измерения физических величин являются одной из важнейших задач физического эксперимента.
Физическая величина – это количественная характеристика процесса, явления или свойства материи. Физическая величина должна иметь определение, содержащее однозначный способ экспериментального нахождения или её расчёта в реальной ситуации.
Измерить физическую величину – значит узнать, сколько раз содержится в ней однородная с ней величина, принятая за единицу измерения.
В результате измерения физической величины получается значение физической величины – именованное число, состоящее из числа и наименования той меры, которой была измерена физическая величина.
1. Прямые и косвенные измерения
Прямыми называют такие измерения, в результате которых непосредственно определяется искомая величина – измерение длины линейкой или штангенциркулем, измерение времени секундомером, температуры – термометром и т.д.
Косвенными называют такие измерения, в которых искомую величину рассчитывают по формуле через величины, полученные в результате прямых измерений.
Примеры косвенно измеряемых величин:
а) объем шара - при прямом измерении его диаметра рассчитывают по формуле  ;
;
б) ускорение силы тяжести при прямом измерении периода  и длины
и длины  математического маятника находят из выражения
математического маятника находят из выражения  ;
;
в) длину световой волны с помощью дифракционной решетки определяют по формуле  , где угол дифракции
, где угол дифракции  получают в результате прямых измерений и т.д.
получают в результате прямых измерений и т.д.
При измерениях неизбежны погрешности. Они обусловлены следующим:
а) недостатками применяемого метода измерения, например, упущением какого-то фактора или неточностью теории, лежащей в основе эксперимента. Это погрешности метода;
б) несовершенством конструкции и неточностью изготовления измерительного инструмента, например, линейки или прибора (гальванометра и т.д.). Это инструментальные погрешности. Следует отметить, что абсолютно точное изготовление инструментов, приборов невозможно;
в) ошибками, возникающими в процессе наблюдений.
2.Абсолютная и относительная погрешности
Из-за наличия погрешностей искомая величина (например, длина, скорость, момент инерции, электрическое сопротивление, длина волны и т.д.) должна быть выражена через величины, полученные в результате наблюдений, и рассчитанную погрешность.
Различают абсолютную и относительные погрешности. Строго говоря, абсолютной погрешностью надо называть величину
 , (1)
, (1)
равную разности истинного значения  искомой величины и какого-то конкретного результата
искомой величины и какого-то конкретного результата 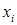 единичного наблюдения (например, пятого, т.е. с
единичного наблюдения (например, пятого, т.е. с  =5).
=5).
Однако не всегда абсолютная погрешность достаточно полно характеризует точность измерений. Так, если при измерении длины комнаты в 5м мы допустим ошибку в 0.5см, то это будет вполне приемлемая точность.
Точностью называют качество измерений, отражающее близость результатов к истинному значению измеряемой величины (количественно точность может быть представлена как величина, обратная относительной погрешности).
Но если с такой же абсолютной погрешностью измерить диаметр карандаша (он около 0.8см), то интуитивно ясно, что точность будет очень низкой. Как же это выразить количественно? Ответ на подобный вопрос позволяет дать относительная погрешность, которую определяют выражением
 , (2)
, (2)
то есть через отношение абсолютной погрешности (результата наблюдения)  к искомой величине
к искомой величине  .
.
Примечание. На практике относительную погрешность определяют через отношение абсолютной или полной погрешности результата серии наблюдений к среднему значению для серии
 . (2,а)
. (2,а)
На примере вышеприведенного измерения длины комнаты  (т.е. 0.1%). Но для диаметра карандаша
(т.е. 0.1%). Но для диаметра карандаша  (т.е. 62.5%). Последняя точность неудовлетворительна.
(т.е. 62.5%). Последняя точность неудовлетворительна.
3.Доверительные границы. Доверительная вероятность (коэффициент надежности)
Опыт показывает, что погрешности могут иметь как положительные, так и отрицательные знаки. Это означает, что величины, полученные в результате наблюдений, будут принимать значения как большие, так и меньшие  , а именно: от
, а именно: от  до
до  .
.
Этот интервал
 , (3)
, (3)
в который должно укладываться большинство значений 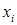 , называют доверительными границами, а
, называют доверительными границами, а  – погрешностью результата наблюдений или измерений.
– погрешностью результата наблюдений или измерений.
В общем случае погрешности имеют случайный характер, поэтому мы можем говорить лишь о вероятности попадания величины 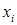 в доверительные границы (3), то есть о доверительной вероятности (коэффициенте надежности)
в доверительные границы (3), то есть о доверительной вероятности (коэффициенте надежности)  . Допустим, что доверительная вероятность
. Допустим, что доверительная вероятность  =0.97. Это означает, что при достаточно большом числе серий, например, по 100 наблюдений в каждой, в среднем в доверительные границы (3) попадает по 97 величин
=0.97. Это означает, что при достаточно большом числе серий, например, по 100 наблюдений в каждой, в среднем в доверительные границы (3) попадает по 97 величин 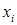 . Отметим, что
. Отметим, что  выбирается экспериментатором самостоятельно. Для наших задач предпочтительно задавать
выбирается экспериментатором самостоятельно. Для наших задач предпочтительно задавать  =0,95.
=0,95.
4.Задача обработки результатов наблюдений
Обратим теперь внимание на то, что ни искомая величина  , ни погрешность
, ни погрешность  , ни доверительная вероятность
, ни доверительная вероятность  неизвестны (правда, последней можно задаться!). Следовательно, задача измерений включает:
неизвестны (правда, последней можно задаться!). Следовательно, задача измерений включает:
а) нахождение величины, близкой по значению с  (искомой величины), и
(искомой величины), и
б) оценку доверительных границ полученных результатов при определенной доверительной вероятности  .
.
5. Систематические и случайные погрешности
Для математической обработки результатов наблюдений и оценки погрешностей весьма существенно то, что погрешности бывают двух видов – систематические и случайные. (Отдельный вид случайных погрешностей, называемых грубыми или просто – промахами – будет рассмотрен на конкретном примере в упр.1 лабораторной работы 1-1). Грубые ошибки (промахи) – ошибки, обусловленные неисправностью средств измерений, неправильным считыванием результата, резкими неучтенными изменениями условий измерений, результатом просчета. Их можно исправить при более тщательном повторении опытов или расчетов.
А. Систематические – это такие погрешности, величина и знак которых в течение эксперимента остаются неизменными, или изменяются по известному закону, который можно установить при анализе методики проведения эксперимента. Эти погрешности существуют при любом измерении.
Систематические погрешности могут быть обусловлены весьма разными причинами, например, недоучетом некоторых постоянно действующих факторов – архимедовой силы (при взвешивании тел в воздухе) или неравноплечности весов, земного магнетизма (при измерении магнитных полей), неточности установки нуля прибора или самого прибора (например, по уровню) и т.д.
Б. Случайные погрешности – это такие погрешности, которые обусловлены рядом мелких, случайно действующих причин, например: небольшими вибрациями почвы и стен зданий; некоторым непостоянством напряжения в электросети; несовершенством процесса отсчета показаний по шкалам приборов во время наблюдений и т.д. Случайные погрешности устранить невозможно, однако их надо уметь рассчитывать, иначе нельзя решить задачу измерений. Влияние случайной погрешности на оценку истинного значения измеряемой величины можно уменьшить многократным повторением измерения.
Отличительные черты случайных погрешностей:
а) они имеют как положительные, так и отрицательные знаки;
б) при весьма большом числе наблюдений абсолютные погрешности одинаковые по модулю, но с противоположными знаками встречаются, как правило, одинаково часто;
в) чем больше (по модулю) величина случайной погрешности, тем она встречается реже.
6. Однократные и многократные измерения
