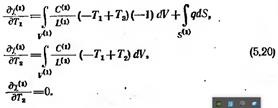Простой пример: перенос тепла в стержне
Глава 5
РАССМОТРЕНИЕ НЕКОТОРЫХ КРАЕВЫХ ЗАДАЧ
С ПОМОЩЬЮ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
В двух предыдущих главах рассматривался вопрос о том, как аппроксимировать непрерывную функцию на отдельном элементе. Кроме того, было показано, как из результатов, полученных для сдельных элементов, составляется множество кусочно-непрерывных функций, необходимое для аппроксимации данной непрерывной функции на всей области. Это множество кусочно-непрерывных функций определяется числовыми значениями узловых величин-. Наша конечная цель — получить для узловых величин такие числовые значения, при которых соотношения для элементов очень точно аппроксимируют некоторый важный физический параметр. На ранней стадии развития метода конечных элементов узловые значения определялись минимизацией интегральной величины, связанной с физическим процессом. В задачах механики деформируемого тела, например, минимизировалась потенциальная энергия системы. В результате уравнения, определяющие элементы, сводились к системе алгебраических уравнений равновесия, которые можно разрешить относительно узловых перемещений. В задачах теории поля (перенос тепла, течение грунтовых вод, расчет магнитных полей и др.) минимизировался некоторый функционал. Этот функционал обладает тем свойством, что любая минимизирующая его функция удовлетворяет как исходным дифференциальным уравнениям, так и 1 различным условиям. Позднее для вывода системы уравнений, определяющих узловые значения, стали использоваться методы взвешенных невязок. Один из них, метод Галёркина, обсуждается в гл. 17.
В данной главе дается вывод уравнений метода конечных элементов, основанный на минимизации некоторой интегральной величины. Мы начнем с рассмотрения небольшого примера, который иллюстрирует вывод уравнений для узловых значений искомой величины в задачах теории поля. Затем на том же примере мы покажем, что процесс минимизации может быть завершен до вычисления интегралов по элементам. После рассмотрения примера дается общий вывод уравнений метода конечных элементов для трехмерных задач теории поля. Глава завершается общим выводом уравнений метода конечных элементов для задач теории упругости. Окончательные результаты как для задач теории поля, так и для задач теории упругости представлены в виде поверхностных и объемных интегралов, которые вычисляются при рассмотрений конкретных областей применения.
При последующем обсуждении предполагается наличие некоторых предварительных знаний стандартной терминологии рассматриваемого материала. Размерности различных величин вместе с их общепринятыми обозначениями приводятся в главах прикладного характера.
Простой пример: перенос тепла в стержне
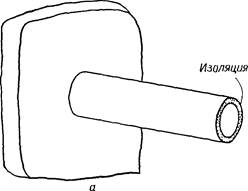 |
Лучше всего процесс минимизации можно проиллюстрировать при рассмотрении простой геометрической фигуры. Рассмотрим одномерный поток тепла в стержне с теплоизолированной боковой поверхностью (фиг. 5.1,а)‘>. К закрепленному в стене
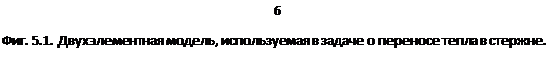 т,
т, 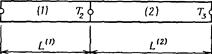
стержня подводится тепловой поток заданной интенсивности q. На свободном конце стержня происходит конвективный обмен тепла. Коэффициент теплообмена h, температура окружающей среды Гоо, °С. Стержень теплоизолирован, так что потерь тепла через боковую поверхность не происходит.
Или в бесконечной пластине. Прим. ред.
Запишем дифференциальное уравнение для распределения температуры внутри стержня:

с граничными условиями
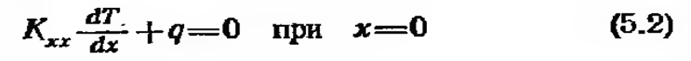
и
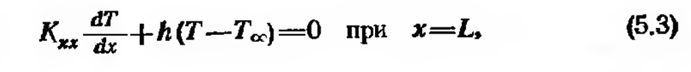
где Кхх — коэффициент теплопроводности материала стержня. Тепловой поток q положителен, если тепло отводится от стержня.
Уравнение (5.1) с приведенными граничными условиями имеет единственное решение. Оно является отправной точкой при получении численного решения методом конечных разностей. Другой метод решения задач переноса тепла основан на вариационном подходе. В вариационном исчислении устанавливается, что для минимизации функционала
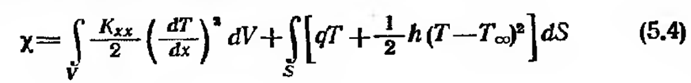
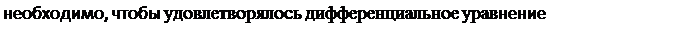

с граничными условиями
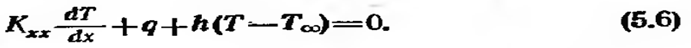
Уравнения (5.5) и (5.6) идентичны исходным уравнениям (5.1) — (5.3), поэтому любое распределение температуры, при котором функционал 1, определяемый формулой (5.4), становится минимальным, также удовлетворяет дифференциальным уравнениям и, таким образом, является решением исходной задачи. Оба граничных условия (5.2) и (5.3) содержатся в (5.6), так как поверхностный интеграл в (5.4) должен быть разбит на два интеграла по каждой из торцовых поверхностей стержня.
о Введение в этот предмет дано в приложении А.
Уравнение (5.4) служит отправной точкой для определения температуры в каждом узле. Мы минимизируем функционал (5.4), используя множество функций элементов, каждая из которых определена на отдельном элементе и выражена через узловые значения. Узловые значения 7’р—неизвестные величины в- нашей формулировке. Так как они определяют значение функционала х, минимизация x должна быть проведена по этим величинам.
Реализация метода конечных элементов начинается с определения подобластей и их узловых точек. Стержень может быть разбит на два линейных элемента (фиг. 5.1,6) с узловыми значениями Ti, Т2 и Г3. Температура внутри элементов находится из формул 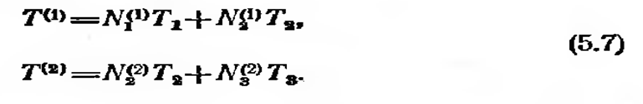 Соответствующие функции формы определены соотношениями
Соответствующие функции формы определены соотношениями
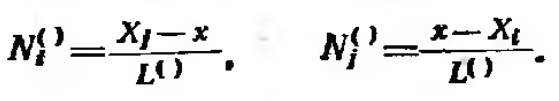
Для рассматриваемого примера функционал представляет собой сумму следующих интегралов:
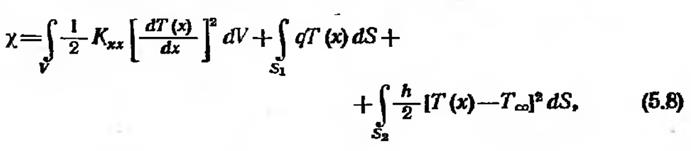 где S1 и S2 — площади поверхностей, на которых заданы q и h. Значение функционала х получается подстановкой температуры Т(х) и вычислением интегралов.
где S1 и S2 — площади поверхностей, на которых заданы q и h. Значение функционала х получается подстановкой температуры Т(х) и вычислением интегралов.
Поверхностные интегралы легко вычисляются, так как подынтегральным выражениям соответствуют узловые значения. Начнем с интеграла, включающего тепловой поток q:
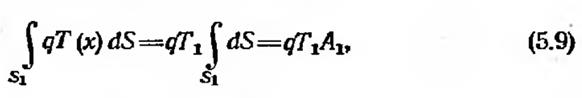
где A1 — площадь поперечного сечения стержня, соответствующая первому узлу. Функция, описывающая изменение температуры Т(х), принимает постоянное значение Т1 в точках сечения, соответствующего первому узлу. Рассмотрим поверхностный интеграл, включающий коэффициент теплообмена h:
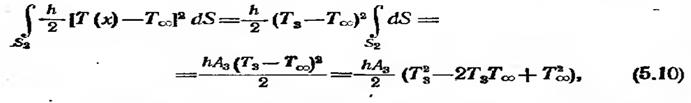 где Аз площадь поперечного сечения стержня и Tз —температура в третьем узле.
где Аз площадь поперечного сечения стержня и Tз —температура в третьем узле.
Объемный интеграл в (5.8) содержит производную от температуры. Дифференцируя (5.7), имеем 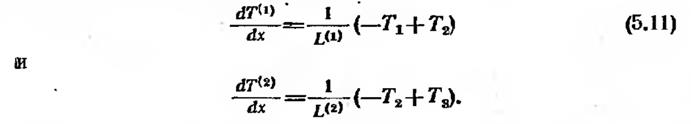
Объемный интеграл должен быть разбит на два интеграла, потому что выражение для dT/dx не сохраняет непрерывности по объему тела в целом. Разделение, подстановка и интегрирование дают
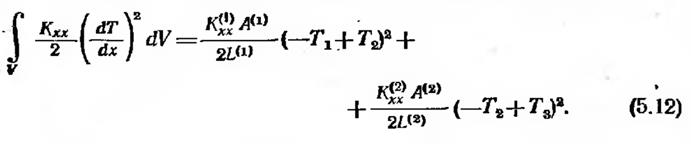
При вычислении интеграла предполагалось, что площадь поперечного сечения каждого элемента посюянна, так что dV=A(e)dx.
Представление объемного интеграла по области в виде суммы интегралов, каждый из которых вычисляется по отдельному элементу, позволяет рассматривать различные свойства материала для различных элементов. Это является важной особенностью метода конечных элементов.
Значение функционала % получается сложением выражений (5.9), (5.10) и (5.12). В результате получается выражение для этого функционала через узловые значения температуры:
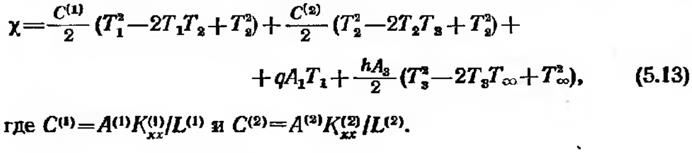 Правильными значениями Т1, T2 и T3 являются те, при которых величина x минимальна, поэтому
Правильными значениями Т1, T2 и T3 являются те, при которых величина x минимальна, поэтому
 |
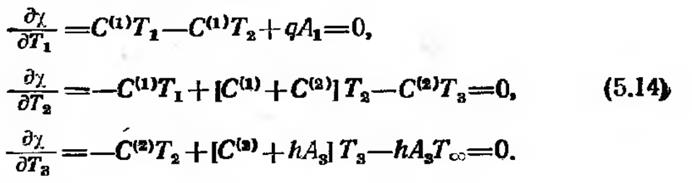
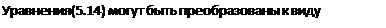
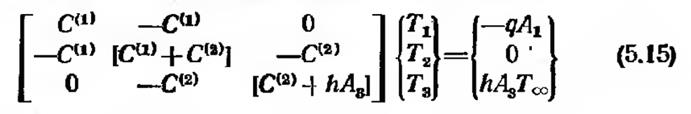
или к более общей матричной форме
[К] {T}-{F}.
Матрицу коэффициентов [/(] в формуле (5.16) обычно называют глобальной матрицейы жесткости. Более уместным было бы назвать ее глобальной матрицей теплопроводности, поскольку мы имеем дело с задачей переноса тепла. Векторный столбец {F} есть глобальный вектор нагрузки.
Последний шаг нашего анализа заключается в задании конкретных значений для физических характеристик материала и получении числовых значений температуры Т1, Т2 и Т3. Пусть
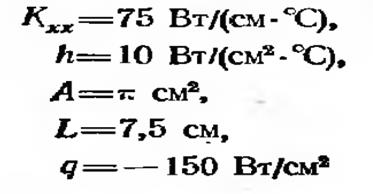
(минус поставлен потому, что тепло подводится к телу) и Т<х,= — 40 °С. Вычисляем коэффициенты
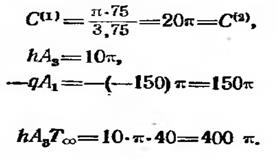
|
|
|
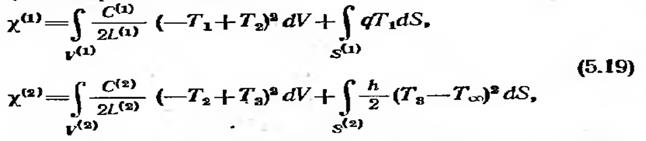
|
|
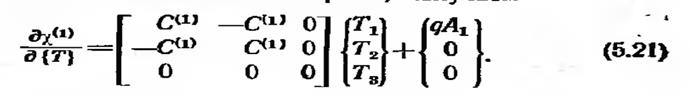
Дифференцируя вторую компоненту , имеем
 |
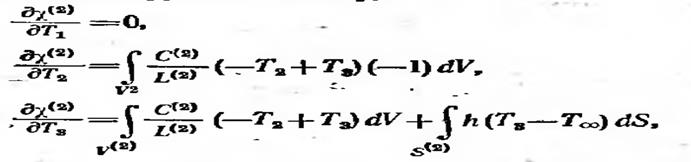
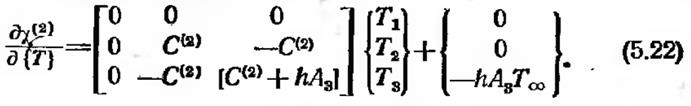
Для минимизации x по узловым значениям необходимо, чтобы выполнялось равенство
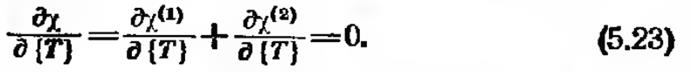
Поэтому если сложить выражения (5.21) и (5.22) и результат приравнять нулю, то получим желаемую систему уравнений
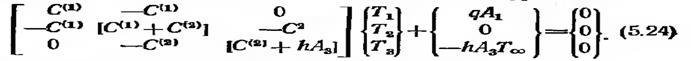
Эта система идентична системе уравнений (5.15).
В изложенном подходе к процессу минимизации важно именно то, что система уравнений может быть получена для отдельных элементов. Суммирование по элементам в соответствии с формулой (5.23) представляет собой очень удобную для машинной реализации процедуру.

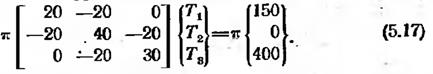 Этим уравнениям удовлетворяют следующие узловые значения температуры: Т1 = 7О, T2 = 62,5, Т3=55.
Этим уравнениям удовлетворяют следующие узловые значения температуры: Т1 = 7О, T2 = 62,5, Т3=55. 
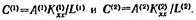 Продифференцируем теперь каждую компоненту x по всем узловым значениям. Начнем с х(1):
Продифференцируем теперь каждую компоненту x по всем узловым значениям. Начнем с х(1):