Логарифмически нормальное (логнормальное) распределение

При логарифмически нормальном распределении нормально распределенным является логарифм (lg t) случайной величины T, а не сама эта величина.

Логарифмически нормальное распределение во многом более точно, чем нормальное описывает наработку до отказа тех объектов, у которых отказ возникает вследствие усталости, например, электронных ламп, подшипников качения и пр.

Если величина lg t имеет нормальное распределение с параметрами: МО U и СКО V, то величина T считается логарифмически нормально распределенной с ПРО, описываемой:

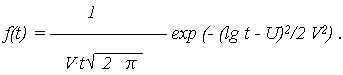(7.7)

Параметры U и V по результатам испытаний принимаются:

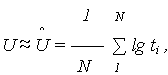	(7.8)
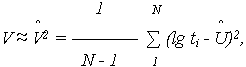	(7.9)

где 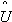и - оценки параметров U и V.

Показатели надежности можно рассчитать по приведенным в разделе 6 выражениям, пользуясь табулированными функциями f(x) и, соответственно, F(x) и 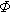(x) для нормального распределения при x = (lg t - U) / V.

Графики изменения показателей надежности при логарифмически нормальном распределении приведены на рис. 7.2.

Числовые характеристики наработки до отказа:

- средняя наработка (МО наработки) до отказа

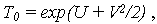(7.10)

Рис. 7.2

- дисперсия наработки до отказа

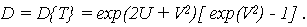(7.11)

Гамма–распределение

Случайная величина наработки до отказа T имеет гамма-распределение с параметрами α (масштабный параметр) и β (параметр формы), где α, β > 0, причем β – целое число, если ее ПРО описывается выражением:

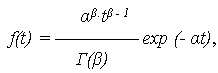(7.12)

где Г(β) = (β - 1)! – гамма-функция Эйлера. Очевидно, что при β = 1 выражение (7.12) упрощается до вида (7.1), соответствующего экспоненциальному распределению.

Гамма-распределение наиболее хорошо описывает распределение суммы независимых случайных величин, каждая из которых распределена по экспоненциальному закону.

При больших β гамма-распределение сходится к нормальному распределению с параметрами: a = β α, b = β / α².

Графики изменения показателей надежности при гамма-распределении приведены на рис. 7.3.

Числовые характеристики наработки до отказа:

- средняя наработка (МО наработки) до отказа

T0 = β/ α,

(7.13)

- дисперсия наработки до отказа

D = D{T} = β/ α2.

(7.14)

Помимо рассмотренных законов распределения, в качестве моделей надежности объектов могут использоваться и другие, например: распределение Вейбулла, хорошо описывающее наработку объектов до отказа по усталостным разрушениям, распределение Релея, распределение Эрланга и др.

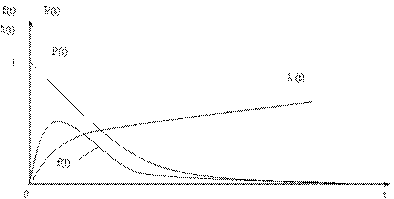
Рис. 7.3

Контрольные вопросы и задачи:

1. Как описывается изменение плотности распределения отказов при экспоненциальном распределении наработки до отказа?

2. Получите расчетное выражение для ВБР, ВО и ИО при экспоненциальном распределении наработки до отказа?

3. Как связаны числовые характеристики наработки до отказа с интенсивностью отказов при экспоненциальном распределении наработки до отказа?

4. Для описания надежности каких объектов используется логарифмически-нормальное распределение?

5. Какой из параметров в выражении плотности распределения отказов при гамма-распределении наработки является параметром формы и параметром масштаба? Известно, что серийно выпускаемая деталь имеет экспоненциальное распределение наработки до отказа с параметром 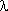= 10 ^-5 час^-1. Деталь используется конструктором при разработке нового прибора. Назначенный ресурс прибора предполагается T_н = 10⁴ час. Определить интересующую конструктора:

1) среднюю полезную наработку детали к моменту T_н;

2) вероятность того, что деталь безотказно проработает в интервале наработки [0, T_н];

3)вероятность того, что деталь безотказно проработает в интервале наработки [10 ³, 10 ⁴ час]?

Ответы: 1) 9.5 · 10 ³ час, 2) 0.905, 3) 0.914.

6. На сборку прибора поступила деталь, прошедшая испытания на надежность. Известно, что наработка до отказа детали подчиняется экспоненциальному распределению с параметром 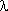= 5*10 ^-5 час ^-1. Определить вероятность того, что при монтаже прибора в него будут поставлены детали, наработка до отказа которых будет находиться в интервале [10 ³, 10 ⁴час]?

Ответ: 0.345.