Закон распределения случайной величины

Содержание

Введение…………………………………………………………………………...3

1. Случайные величины……………………………………………………....…..4

2. Классификация случайных величин……………………………………....…..4

3. Закон распределения случайной величины…………………………………...5

4. Функция распределения случайной величины и ее свойства……………….6

5. Плотность распределения вероятностей……………………………………...8

6. Вероятность попадания непрерывной случайной величины в заданный интервал……………………………………………………………………………9

7. Числовые характеристики непрерывных случайных величин……………...9

7.1 Математическое ожидание случайной величины, его вероятностный смысл и свойства……………………………………………………….…………9

7.2 Дисперсия случайной величины и ее свойства……………………………13

7.3 Среднеквадратическое отклонение………………………………………..16

8. Статистические гипотезы………………………………………………….....17

8.1 Способы проверки некоторых статистических гипотез……………….....18

8.2 Сравнение двух средних генеральных совокупностей…………………...19

8.3 Сравнение двух вероятностей биномиальных распределений…………...21

8.4 Критерий согласия Пирсона………………………………………………...22

9. Практическая часть…………………………………………………………...25

9.1 Часть I………………………………………………………………………...25

9.2 Часть II…………………………………………………………………….....30

Заключение………………………………………………………………………38

Список литературы

Введение

Одним из основных понятий в теории вероятностей является понятие случайной величины. Случайная величина является числовой характеристикой результата эксперимента, которая принимает свои значения в зависимости от элементарного события. Примером случайной величины могут быть: число очков, выпадающих при одном бросании игральной кости, число граждан, которые имеют высшее образование среди взятых наугад n человек, число бракованных изделий в партии из N штук, время безотказной работы прибора и т.д.

1.

Случайные величины

Одним из важнейших понятий теории вероятностей является понятие случайной величины.

Случайной величиной называется переменная величина, которая в зависимости от исхода испытания случайно принимает одно значение из множества возможных значений.

Случайная величина обычно обозначается прописной латинской буквой 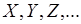, ее конкретные значения – строчными буквами .

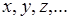Случайной величиной называется функция 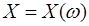, определенная на множестве элементарных событий , .

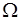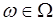Классификация случайных величин

Случайные величины делятся на дискретные и непрерывные. Величина называется дискретной, если она может принимать определенные, фиксированные значения.

Случайная величина называется непрерывной, если она может принимать значения, сколь угодно мало отличающиеся друг от друга.

Пусть дискретная случайная величина 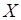может принимать 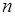значений: 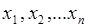. Для полной характеристики этой случайной величины должны быть заданы еще и вероятности появления указанных значений .

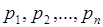Закон распределения случайной величины

Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения

данной случайной величины.

Законом распределения случайной дискретной величины называется совокупность пар чисел ( 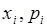), где 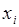– возможные значения случайной величины, а 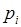– вероятности, с которыми она принимает эти значения, причем .

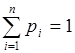В простейших случаях закон распределения случайной величины 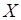удобно задавать таблицей:

Таблица

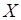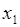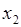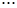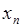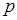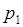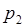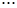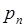Заметим, что таблицу значений дискретной случайной величины 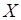, если это целесообразно, формально всегда можно пополнить конечным набором любых чисел, считая их значениями 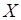с вероятностями, равными нулю.

Случайные величины 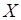и 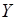называются независимыми, если возможные значения и закон распределения каждой из них один и тот же при любом выборе допустимых значений другой и не зависит от того, какое возможное значение приняла другая величина. В противном случае эти величины называются зависимыми. Несколько случайных величин называются взаимно независимыми, если возможные значения и законы распределения любой из них не зависят от того, какие возможные значения приняли остальные случайные величины.