Соприкасающаяся плоскость и нормали
Если взять в качестве 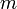 плоскость, проходящую через точку
плоскость, проходящую через точку 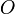 кривой
кривой 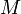 , то условие соприкосновения при
, то условие соприкосновения при  определяет соприкасающуюся плоскость кривой (рис. 1). Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.
определяет соприкасающуюся плоскость кривой (рис. 1). Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость. Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.
Пусть 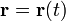 — уравнение кривой. Тогда уравнение
— уравнение кривой. Тогда уравнение 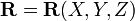 её соприкасающейся плоскости определяется из соотношения:
её соприкасающейся плоскости определяется из соотношения:
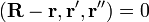
В координатах оно имеет вид:
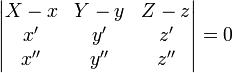
Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Также нормалью и бинормалью для краткости могут называть единичные векторы вдоль этих прямых (при этом направление вектора главной нормали обычно выбирают совпадающим с направлением вектора кривизны кривой[1]).
Векторное уравнение бинормали в точке, отвечающей значению  параметра
параметра 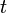 , имеет вид:
, имеет вид:
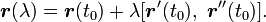
Направление главной нормали может быть получено как двойное векторное произведение: 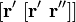 .
.
Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке 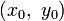 имеет следующий вид.
имеет следующий вид.
§ Параметрическое задание: 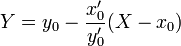
§ Явное задание: 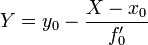
§ Неявное задание: 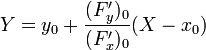
Кривизна кривой.
Плоскую кривую линию можно рассматривать как траекторию движения точки в плоскости; точка движется по касательной к кривой линии, обкатывая эту кривую без скольжения.
Движение точки вдоль кривой а связано с непрерывным изменением двух величин: расстояния S, на которое удалена точка от начального положения и углаa поворота касательной относительно начального положения.
Если с увеличением пути S непрерывно увеличивается и a , кривая называется простой.
Угол a (угол смежности) между касательными в двух бесконечно близких точках кривой, отнесенный к длине дуги между этими точками, определяет степень искривленности кривой линии, т.е. определяет кривизнукривой k.
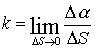 ,
,
предел отношения угла смежности касательных к соответствующей дуге.
Кривизна прямой в любой её точке равна нулю.
Кривизна произвольной кривой линии в различных точках различна, в отдельных точках она может быть равна нулю. Такие точки называются точками спрямления.
Кривизна в каждой из точек плоской кривой а определяется с помощью соприкасающейся в этой точке окружности
Соприкасающейся окружностью или кругом кривизны в данной точке называется предельное положение окружности, когда она проходит через данную точку и две другие бесконечно близкие к ней точки.
Центр соприкасающейся окружности называется центром кривизны кривой в данной точке, а радиус такой окружности – радиусом кривизны кривой линии в данной точке.
