Синтез управления для линеаризованной системы с учетом внешних неопределенных ограниченных возмущений

Теорема 1.3. Решение задачи

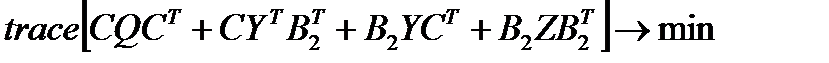
при ограничениях

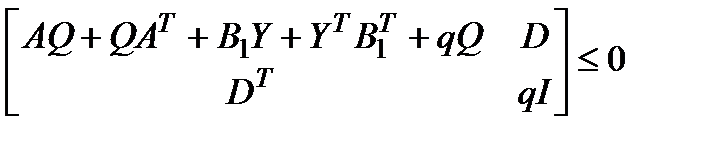(1.10)

, (1.11)

где минимизация проводится по матричным переменным , скалярному параметру q>0, определяет при каждом q матрицу предельного инвариантного эллипсоида для вектора состояния x(t), матрицу предельного ограничивающего эллипсоида для вектора выхода z(t) системы (1.4) и зависимую от времени матрицу коэффициентов соответствующего регулятора по состоянию .

Для решения задачи оптимизации при каждом фиксированном значении параметра q из заданного диапазона (задачи полуопределенного программирования) используется программное обеспечение CVX. Текст программы для перебора с заданным шагом изменения параметра q и синтеза регулятора из условия нахождения минимального по критерию следа ограничивающего предельного эллипсоида для вектора выхода представлен ниже.

step = 0.1;

begin_val = 3;%0.1;%

end_val = 3.4;%

min_tr_Z = 1000000;

figure (1)

% Оптимизация по параметру q путем перебора с уменьшающимся шагом

while step>0.001

for q = begin_val:step:end_val

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Zs(1,1) symmetric;

variable Ys(1, n1) ;

variable bet ;

minimize( trace(C*Qs*C'+C*Ys'*B2'+B2*Ys*C'+B2*Zs*B2'))

%minimize( trace(Qs))

subject to

Qs >= eye(2)*1e-3;

[A*Qs + Qs*A'+B1*Ys+Ys'*B1'+q*Qs D;

D' -q*eye(l)]< 0; %условие асимптотич устойчивости

[Zs Ys;

Ys' Qs]>=0;

cvx_end

Qsf = double(Qs)

Y=double(Ys)

K=Y/Qsf

Z=double(Zs);

trZ=trace(C*Qsf*C'+C*Y'*B2'+B2*Y*C'+B2*Z*B2');

if min_tr_Z > trZ

min_tr_Z = trZ

Q_min = Qsf;

K_min=K;

q_min = q

end;

end;

step = step*0.5;

begin_val = q_min-2*step;

end_val = q_min+2*step;

end;

Q1=Q_min

K1=K_min

q1=q_min

Для рассматриваемой системы с теми же значениями параметров была найдена матрица

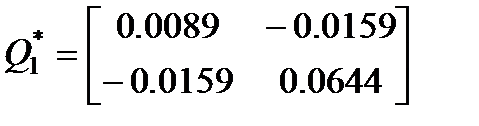
минимального инвариантного эллипса и соответствующий регулятор с постоянными коэффициентами K₁=[–14.0108 –7.4779] при q₀=3.5969. На рисунке 1.2 показаны найденные минимальные инвариантные эллипсы для линеаризованной системы с модальным регулятором (штриховая линия) и системы с регулятором, полученным в результате решения задачи оптимизации с ЛМН (сплошная линия). Из рисунка видно, что регулятор, синтезированный для линеаризованной системы с неопределенными ограниченными возмущениями значительно эффективнее подавляет внешние неопределенные возмущения, чем модальный регулятор. В то же время, если задать для модального синтеза собственные значения матрицы замкнутой системы в виде 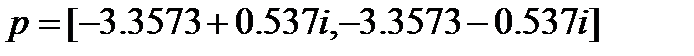, т.е. такие же как у системы с регулятором K₁, то можно получить модальный регулятор так же эффективно подавляющий внешние неопределенные возмущения.

Рисунок 1.2. Минимальные инвариантные эллипсы системы с модальным регулятором (штриховая линия) и с регулятором, подавляющим внешние возмущения, с ограничением выхода (сплошная линия)

Матрица замкнутой системы .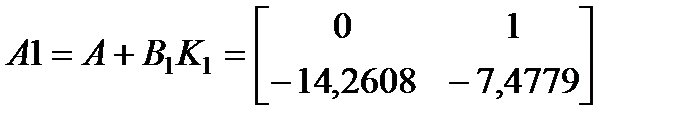

Рисунок 1.3. Сечения эволюционирующего инвариантного эллипса для системы с регулятором K₁

На рисунке 1.3 показаны сечения эволюционирующего инвариантного эллипса для системы с регулятором K₁, полученные в результате численного интегрирования МСС (1.9) с начальной матрицей 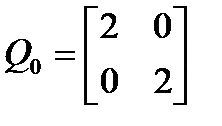. Решение сошлось за t<20c к минимальному предельному инвариантному эллипсу с матрицей .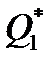