Модель озонатора без системы охлаждения
При турбулентном режиме течения газа из-за сильного вихревого потока распределение температуры в разрядном промежутке можно считать по формуле (следует из уравнения теплового баланса энергии,(3)):
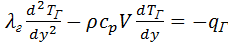 , (7)
, (7)
Где q – объемная плотность мощности тепловыделения в газе, 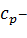 коэффициент теплоемкости газа при постоянном давлении,
коэффициент теплоемкости газа при постоянном давлении, 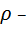 плотность газа.
плотность газа.
Это уравнение учитывает теплопроводность газа, теплоперенос потоком газа и тепловыделение в нем за счет электрического разряда. 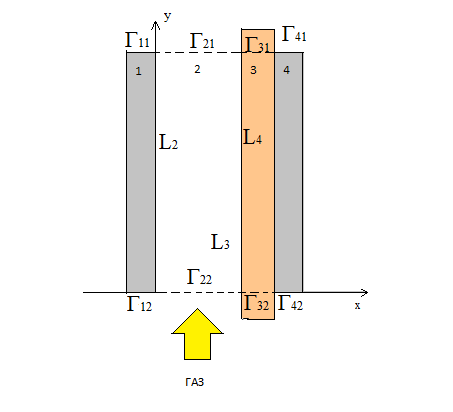
Граничные условия для уравнения (3-5,7), ТА – исходная температура газа:
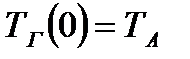 (8.1)
(8.1)

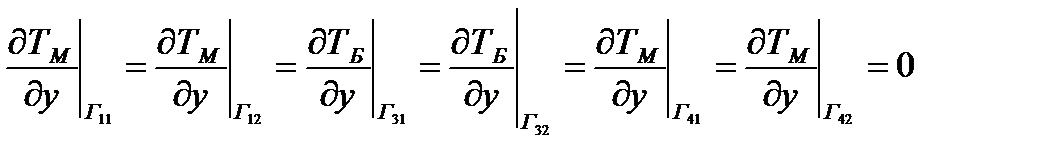
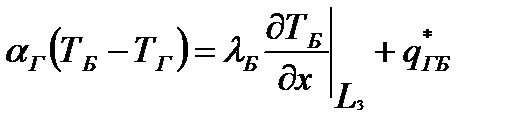
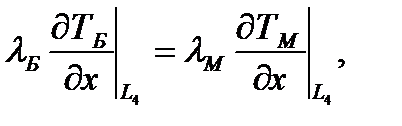


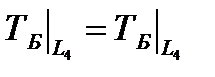 .
.
Граничные условия на выходе с обоих боков будет выглядеть так:
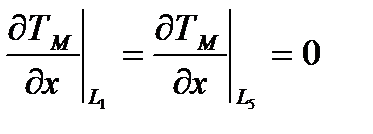 .
.
А на выходе из разрядного промежутка 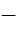
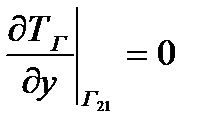 (8.2) (8)
(8.2) (8)
Здесь 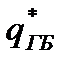 - отражает поверхностное выделение тепла, приходящееся на единицу площади на границе газ-барьер.
- отражает поверхностное выделение тепла, приходящееся на единицу площади на границе газ-барьер.
Таким образом, построена модель тепловых явлений в элементах озонатора, представленная совокупностью системы уравнений (3)-(5) , (7) и граничных условий (8).
На данный момент очень сильно вырос интерес к барьерным электрическим озонаторам именно с турбулентным течением озонируемого газа. Это связано со многими фактами, но в основном использование данного режима позволяет использовать поток, в некоторых случаях, в качестве основного теплоотводящего элемента, что в свою очередь решает проблему с громоздкой системой охлаждения. Другим не маловажным “плюсом” турбулентного режима является хорошая перемешиваемость озонируемого газа, а так же самоочистка разрядного промежутка от кристаллизующейся пятиокиси азота.
Реализуем основную часть модели распределения температуры
Для того чтобы реализовать данную модель распределения температуры, без системы охлаждения, нужно решить уравнение (7), с граничными условиями (8.1) и (8.2).
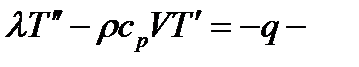 линейное дифференциальное уравнение 2-го порядка, которое можно свести к 1-му порядку.
линейное дифференциальное уравнение 2-го порядка, которое можно свести к 1-му порядку.
Для этого сделаем замену:
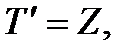
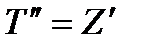 *
*
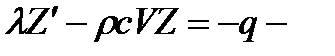 линейное дифференциальное уравнение.
линейное дифференциальное уравнение.
Решим его заменой переменных:
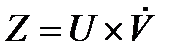 ;
; 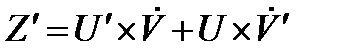 **
**
Получим:
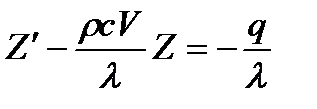
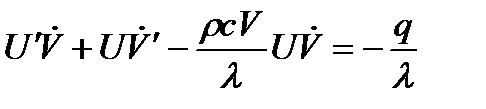
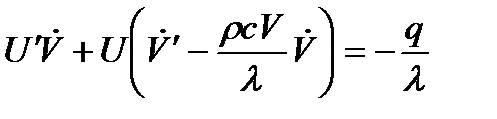 (a)
(a)
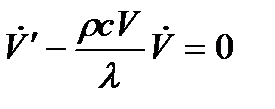 - дифференциальное уравнение с разделяющимися переменными
- дифференциальное уравнение с разделяющимися переменными
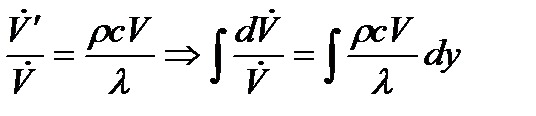
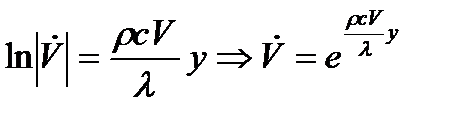 (b)
(b)
Из (а) и (b) следует:
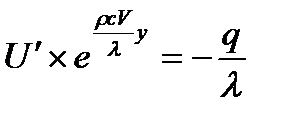
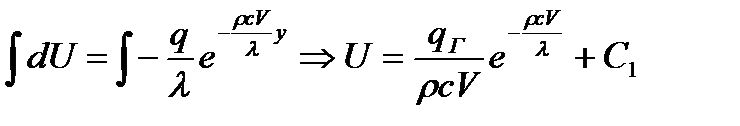


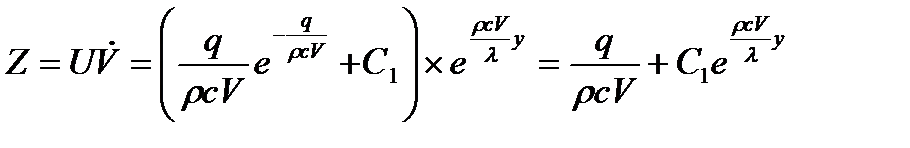

Заключение
В работе рассмотрены строение и виды озонаторов, а также режимы течения газа в них. Рассмотрены математические модели тепловых процессов в барьерном электрическом озонаторе, в том числе модель теплоотвода из разрядного промежутка.
Модель описывает охлаждение озонатора «Элита», предназначенного для использования в полярных и северных условиях, а также других озонаторов.
Модель позволяет создавать озонаторы большей интенсивности, чем изготавливаемые в настоящее время зарубежной и отечественной промышленностью.
Список литературы
1. Кузнецов В. А. Математическое моделирование процессов в барьерном электрическом озонаторе: Теория и практика. – Москва–Ижевск: Институт компьютерных исследований, 2004. – 194 с.
2. Тихонов А. Н., Самарский А. А. Уравнения математической физики. –М.: Наука, 1972. – 735 с.
3. Филиппов Ю. В., Вобликова В. А., Пантелеев В. И. Электросинтез озона. – М., 1987. –237 с.
4. http://ru.wikipedia.org
