Как определяется скручивающий момент по мощности, передаваемой валом, и по частоте вращения?

Скручивающий момент вычисляется по следующей формуле

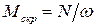,(5.1)

где 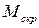– скручивающий момент, Н·м.; N – мощность, Вт; 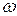– угловая частота вращения вала, рад/c.

Если 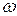измеряется в оборотах в минуту, то формула (5.1) принимает вид:

.

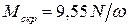5.4. Какие допущения положены в основу теории кручения круглых стержней?

Считается, что при малых углах закручивания вала:

· поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (это допущение принято называть гипотезой плоских сечений или гипотезой Бернулли);

· радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины;

· длина вала в результате закручивания также не изменяется.

Таким образом,поперечное сечение вала ведет себя при кручении, как жесткий диск, итогдадеформациюкручения можно рассматривать как результатсдвигаодного поперечного сечения относительно другого. Следовательно, в точках поперечного сечения вала возникают только касательные напряжения.

Теория кручения, основанная на перечисленных выше допущениях, хорошо подтверждается многочисленными опытными данными. Одним из первых исследователей, экспериментально изучавших кручение круглых стержней, был французский ученый Шарль Огюстен Кулон (Coulomb, 1736 – 1806 гг.).

5.5. Как ведут себя стержни прямоугольного поперечного сечения при кручении?

Упомянутые допущения, сформулированные для круглого вала, не могут быть приняты для стержня прямоугольного поперечного сечения. При кручении такого стержня отдельные точки поперечного сечения перемещаются вдоль его оси. И поэтому все сечение, в целом, перестает быть плоским (оно коробится). Происходит так называемая депланация поперечного сечения стержня.

Эта задача является значительно более сложной по сравнению со случаем кручения стержня круглогопоперечногосечения и методами сопротивления материалов она не может быть решена.

5.6. 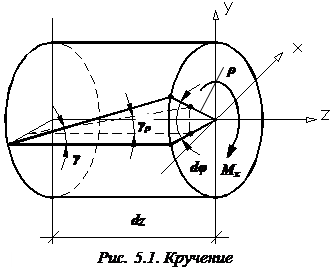Какая зависимость существует между углом сдвига и относительным углом закручивания?

Рассмотрим часть вала длиной 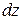. Предположим, что правое поперечное сечение вала провернулось на угол 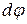относительно левого сечения. Для произвольного продольного волокна, отстоящего от оси вала на расстоянии 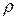, возникнет абсолютный сдвиг, равный 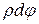(рис. 5.1).

Тогда угол сдвига

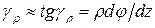. (5.2)

Входящая в формулу (5.2) величина

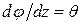
называется относительным углом закручивания.

Таким образом, между углом сдвига и относительным углом закручивания существует следующая зависимость:

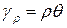. (5.3)

5.7. Как записывается закон Гука при кручении?

Так же, как и при сдвиге:

,

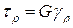или, с учетом зависимости (5.3),

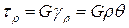, (5.4)

то есть, касательные напряжения в произвольной точке поперечного сечения вала, отстоящей от центра тяжести сечения на расстоянии 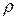, пропорциональны относительному углу закручивания.

При этом в точках, равноудаленных от центра тяжести поперечного сечения, численные значения касательных напряжений одинаковы.

Из формулы (5.4) следует, что касательные напряжения, возникающие в поперечном сечении вала при кручении, изменяются по линейному закону (пропорционально 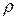– расстоянию от точки, в которой мы вычисляем напряжения, до центра тяжести). Они равны нулю в центре вала и достигают максимального значения 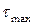в точках контура поперечного сечения (рис. 5.2).

Из рис. 5.2 видно, что средняя часть поперечного сечения вала практически не участвует в сопротивлении кручению. В связи с этим на практике находят широкое применение полые валы. Такие валы, при той же площади поперечного сечения F, могут воспринять больший скручивающий момент.

5.8. 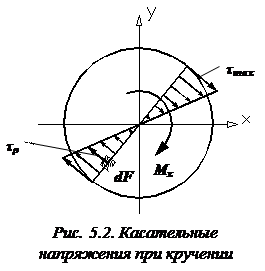Как выражается крутящий момент через касательные напряжения, возникающие в поперечном сечении вала?

При повороте поперечного сечения каждая его точка (кроме, разумеется, точки, лежащей на оси вала) перемещается по некоторой дуге окружности радиуса 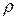. Поэтому направление касательного напряжения, возникающего в этой точке, должно быть перпендикулярно к радиусу 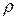, проведенному в эту точку.

Элементарная внутренняя сила, возникающая на площадке 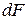(см. рис. 5.2), равна 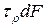, а ее момент относительно оси 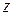(или центра тяжести поперечного сечения вала):

.

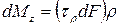Суммируя эти элементарные моменты по всей площади, получим выражение для крутящего момента, возникающего в поперечном сечении вала:

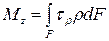. (5.5)