Дискретное преобразование Лапласа
Для использования импульсных систем автоматического регулирования, а также в других прикладных задачах, связанными с решетчатыми функциями и разностными уравнениями, используется преобразование, определяемое формулой
F*(q)= 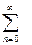 e-qnf[n] (1)
e-qnf[n] (1)
Где q=s+ 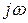 - комплексная переменная.
- комплексная переменная.
Оно называется дискретным преобразованием Лапласа, а также D-преобразованием и сокращенно обозначается D{f[n]}, т.е.
F*(q)=D{f[n]}
Функция F*(q), определяемая (1) называется изображением. Дискретное преобразование Лапласа может быть определено и для смещенных решетчатых функций в соответствии с формулой
F*(q, e)=D{f[n, e]}= 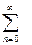 e-qnf[n, e] (2)
e-qnf[n, e] (2)
Где e- параметр, принимающий значения на отрезке [0,1].
Наряду с D - преобразованием в теории автоматического регулирования применяется так называемое Z-преобразование, определяемое (1), (2), в которых используется новая переменная
z=eq
F*z(z)= 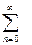 z-nf[n]
z-nf[n]
Z-преобразование принято обозначать так
Z{f[n]}=F*z(z)
Если известно изображение F*(q) некоторой решетчатой функции, то соответствующее изображение F*z(z) может быть найдено с помощью замены комплексной переменной q по формуле
q=ln z®F*z(z)= F*(ln z)
Аналогично можно определить изображение F*(z)
F*(q)= F*z(eq).
Таким образом, принципиальной разницы между D - преобразованием и Z-преобразованием не существует. Все основные свойства Z-преобразования могут быть получены из соответствующих свойств D-преобразования.
Отметим, что D-преобразование решетчатой функции f[n] можно рассматривать как обычное преобразование Лапласа функции, состоящей из последовательности смещенных дельта-функций
g(t)= 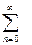 f[n]d(t-n)
f[n]d(t-n)
Применяя к этой функции преобразование Лапласа на основании фильтрующего свойства d-функции получим
L[g(t)]= 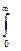 g(t)e-qtdt=
g(t)e-qtdt= 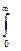
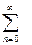 f[n] d(t-n)e-qtdt=
f[n] d(t-n)e-qtdt= 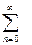 f[n]
f[n] 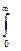 d(t-n) e-qtdt=
d(t-n) e-qtdt=
= 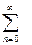 f[n] e-qn=D{f[n]}
f[n] e-qn=D{f[n]}
Формула обращения определяет решетчатую функцию f[n] по заданному изображению F*(q)
f[n]=D-1{F(q)} (n³0)
D-1-преобразование определяется формулой
f[n]= 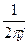

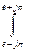 F*(q)eqndq (n³0)
F*(q)eqndq (n³0)
где с>de; de- абсцисса абсолютной сходимости.
Для смещенных решетчатых функций формула D-1-преобразования имеет вид
f[n,e]= 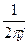
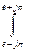 F*(q, e)eqndq
F*(q, e)eqndq
Наконец, формула обращения Z-преобразования, которая получается из предыдущей путем замены z=eq
f[n]= 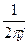
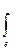 F*(z, e)zn-1dt
F*(z, e)zn-1dt
интегрирование производится по окружности c радиуса eс, где c>se в положительном направлении. К последующему выражению можно применить теорему о вычетах, согласно которой получим
f[n]= 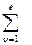 ResF*(z,e)zn-1 ½z=zn,
ResF*(z,e)zn-1 ½z=zn,
где z= zn - полюса функции F*(z, e)zn-1, лежащие внутри окружности с.
Однако более удобен путь разложения функции F*[z,e] в ряд Лорана по убывающим степеням z. Коэффициенты при соответствующих степенях z равны значениям оригинала в дискретные моменты времени t=nT, где n=0,1,2… Т. к. Z - преобразование представляет собой дробно-рациональную функцию, то разложение в ряд Лорана можно делать делением числителя на знаменатель выражения F*(z,e).
Таким образом, проводя разложение в ряд
F*(z,e)=a0(e)+a1(e)z-1+…+ an(e)z-n+…+…
Получаем f[n, e]=an(e), n=0, 1, 2…
Примеры
1. F*(q)=D{1[n]}= 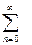 e-qn1[n]
e-qn1[n]
при условии, что Re q>0 этот ряд сходится, т.к. сумма ряда, изображение функции 1[n], равна
F*(q)= 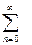 e-qn=
e-qn= 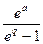 , абсцисса абсолютной сходимости sl =0
, абсцисса абсолютной сходимости sl =0
F*(z)= 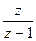
2. D{ea n}, a- любое вещественное число
D{ ea n }= 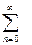 e-q nea n=
e-q nea n= 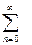 e-n(q-a)=
e-n(q-a)= 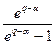 =
= 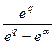 ,
,
т.е. F*(q)= 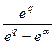 , а F/(z)=
, а F/(z)= 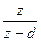 , где d=ea
, где d=ea
Здесь абсцисса абсолютной сходимости sl=a
Найти оригинал, соответствующий изображению.
3. F*z(z)= 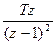 .
.
4. Разложим F*(z) в ряд Лорана путем деления числителя на знаменатель
_Tz ½Z2-2z+1
Tz-2T+Tz-1 z-1+2Tz-2+3Tz-3+…
0_2T-Tz-1
2T-4Tz-1+2Tz-2
0_3Tz-1-2Tz-2
3Tz-1-6Tz-2+3Tz-3
0 4Tz-2-3Tz-3
получим f[n]=an=nT, n=0, 1, 2,… чему соответствуе непрерывная функция f(t)=t при T=1
4. F*z(z)= 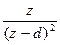 , где d=e-b;
, где d=e-b;
f[n]=ne-b(n-1). Здесь Т=1
