Перпендикуляр к стороне угла
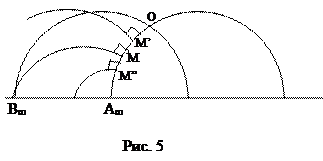 Для любого угла, образованного пересечением прямых ОА¥ и ОВ¥, рис. 5, на любой из его сторон (например, на стороне ОА¥) существует такая точка М, что перпендикуляр, восстановленный к ОА¥ из точки М, будет параллелен второй стороне угла OB¥, рис. 5: MB¥^OA¥, и MB¥||OB¥. При этом, всякий перпендикуляр, выходящий из точки М’ÎОМ, пересекает противоположную сторону угла ОВ¥, а всякий перпендикуляр, восстановленный из точки M"ÎMA¥, не имеет общих точек со стороной OB¥, рис. 5.
Для любого угла, образованного пересечением прямых ОА¥ и ОВ¥, рис. 5, на любой из его сторон (например, на стороне ОА¥) существует такая точка М, что перпендикуляр, восстановленный к ОА¥ из точки М, будет параллелен второй стороне угла OB¥, рис. 5: MB¥^OA¥, и MB¥||OB¥. При этом, всякий перпендикуляр, выходящий из точки М’ÎОМ, пересекает противоположную сторону угла ОВ¥, а всякий перпендикуляр, восстановленный из точки M"ÎMA¥, не имеет общих точек со стороной OB¥, рис. 5.
Четвертый признак конгруэнтности треугольников.
В абсолютной геометрии без привлечения аксиомы параллельности доказываются три признака конгруэнтности треугольников. В планиметрии Лобачевского справедлив еще один, четвертый признак. Если три угла одного треугольника конгруэнтны соответствующим трем углам второго треугольника, то эти треугольники конгруэнтны, [7].
Вывод 2.
Рассмотренные выше неевклидовы отношения 1-4 между прямыми на плоскости Лобачевского являются логическим следствием 15 аксиом планиметрии Лобачевского и реализуются в модели Пуанкаре L2.
О роли открытия неевклидовой геометрии.
Открытие мыслимой неевклидовой геометрии задолго до построения ее реализаций и последовавшие затем открытия ее реализаций Гауссом, Клейном, Бельтрами и Пуанкаре явились прологом пересмотра многих устоявшихся фундаментальных понятий в теории познания. Вначале подверглись анализу идеи и методы доказательства в классической математике и математической логике. Это привело к рождению теории множеств и развитию дедуктивного формализма в математике на новом структурном уровне. Новые геометрические идеи математического формализма подняли научный уровень теоретической физики, а затем и всего естествознания.
В современной науке понятие реализации или модели некоторой системы аксиом используется для проверки основных требований, предъявляемых к аксиоматическому методу в моделировании вообще и в математическом моделировании в частности.
Вывод 3.
Открытие и построение неевклидовой геометрии предшествовало, а затем и сопутствовало развитию современного математического формализма. Роль математического формализма в современной науке не сводится только к формированию математического аппарата. Многие законы, открытые в теории математического формализма, т.е. в математических языках, моделируют интеллектуальную деятельность вообще и исследовательскую деятельность в частности.
Формирование математических текстов на основе дедуктивного метода, т.е. построение теории на базе системы аксиом, должно удовлетворять некоторым законам - свойствам аксиоматических систем. К изучению этих законов мы приступаем в следующей главе.
“Лучший метод для предвидения будущего развития математических наук заключается в изучении истории и нынешнего состояния этих наук”
Анри Пуанкаре.
ГЛАВА II
Свойства аксиоматических систем.
Математические структуры и аксиоматические теории.
Понятие отношений между объектами.
Принято считать, что всякое отношение выражает связи между объектами или, что то же, элементами x, y, … , некоторых множеств A'x, B'y, … . Отношения между двумя элементами xÎA и yÎB называют двухместными или бинарными отношениями. Все такие отношения будем обозначать Ð(x,y), xÎA, yÎB. Отношение Ð (x,y) можно представлять разными способами: описывать словами, изображать чертежами и задавать формулами. Удобным является «язык» множеств. Всякое отношение Ð(x,y) определяет множество p(x,y) упорядоченных пар (x,y) некоторых элементов xÎA и yÎB по следующему правилу:
(x,y) Îp Û {выполняется Ð (x,y)} (1)
Множество упорядоченных пар (x,y) "xÎA и "yÎB называется декартовым произведением множеств A и B и обозначается A´B.
Следствие 1.
Всякое бинарное или двухместное отношение Ð(x,y) между элементами x, y двух множеств A'x и B'y представляется некоторым подмножеством P(x,y)ÌA´B по закону (1). Обратно, всякое подмножество PÌ A´B по этому же закону (1) представляет некоторое отношение Ð(x,y).
Пример 1.
Пусть A=B=R - множество действительных чисел. Тогда R´R есть декартово произведение евклидовых прямых. Это произведение представляет собой арифметическую модель евклидовой плоскости. (Другими словами, множество числовых упорядоченных пар (x,y), "xÎR, "yÎR представляет все точки евклидовой плоскости.)
Определение.
Отношение Ð(x,y) между элементами множества M называется отношением эквивалентности, обозначим его Ð(x,y)º(x~y), если выполняются три условия:
1. Рефлексивности x~x;
2. Симметричности: если x~y, то y~x;
3. Транзитивности: если, x~y, y~z, то x~z.
Примеры отношений эквивалентности: числовые равенства, конгруэнтность фигур, подобие фигур, параллельность прямых и т.д.
Любое отношение эквивалентности Ð(x,y) для (x,y)ÎM´M определяет новое множество классов эквивалентности: два элемента x,yÎM попадают в один класс тогда и только тогда, когда x~y. Множество классов эквивалентности называется фактор множеством M по отношению Ð и обозначается M/Ð или M/p, что равносильно в силу следствия 1.
Отношение эквивалентности разбивает множество M на непересекающиеся классы. Обратно, всякое разбиение M на непересекающиеся классы задает на M отношение эквивалентности. Действительно, если M=M 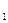 ÈM
ÈM 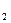 È…ÈM
È…ÈM 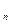 … и M
… и M 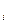 ÇM
ÇM 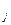 =Æ при i¹j, то отношение принадлежности элементов одному классу (xÎM
=Æ при i¹j, то отношение принадлежности элементов одному классу (xÎM 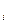 )Ù(yÎM
)Ù(yÎM 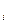 )ºÐ(x,y) удовлетворяет условиям 1) - 3) отношения эквивалентности.
)ºÐ(x,y) удовлетворяет условиям 1) - 3) отношения эквивалентности.
Следствие 2.
Задание отношения эквивалентности на некотором множестве равносильно разбиению этого множеств на непересекающиеся подмножества.
Аналогично двухместному, определяются n–местные отношения между элементами x 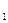 ÎA
ÎA 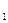 ,…,x
,…,x 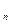 ÎA
ÎA 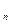 некоторых множеств A
некоторых множеств A 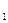 , …, A
, …, A 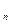 .
.
Декартово произведение A 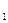 ´A
´A 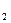 ´…´A
´…´A 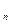 есть множество упорядоченных наборов (x
есть множество упорядоченных наборов (x 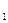 ,x
,x 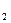 ,…,x
,…,x 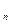 ) элементов x
) элементов x 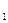 ÎA
ÎA 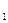 ,…,x
,…,x 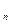 ÎA
ÎA 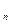 . n–местное отношение Ð(x
. n–местное отношение Ð(x 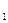 ,…,x
,…,x 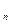 ) представляется некоторым подмножеством pÌ A
) представляется некоторым подмножеством pÌ A 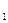 ´A
´A 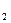 ´…´A
´…´A 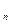 по закону
по закону
{ Ð(x 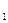 ,x
,x 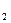 ,…,x
,…,x 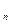 ) выполняется} Û (x
) выполняется} Û (x 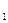 ,x
,x 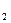 ,…,x
,…,x 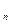 )ÎpÌ A
)ÎpÌ A  ´A
´A  ´…´A
´…´A