Построение общей модели временного ряда

Порядок моделирования рассмотрим на примере построения аддитивной модели ряда динамики, исходные данные которого приведены в таблице 1. .

Аддитивную модель ряда динамики можно представить в виде формулы:

F = T + S + E

где: F – прогнозируемое значение;

Т – тренд;

S – сезонная компонента;

Е – ошибка

Графическое изображение данного ряда динамики показано на рисунке 1, откуда видно, что ряд имеет слабо выраженную линейную тенденцию и сезонные колебания с периодом, равным трем месяцам (одному кварталу).

Таблица 1 - Доля расходов населения на покупку товаров и оплату услуг от величины помесячных денежных доходов населения условного региона

Месяц, t	Доля расходов на покупку товаров и оплату услуг в % от общего среднедушевого дохода, yt
Январь	76,6
Февраль	69,6
Март	64,3
Апрель	64,3
Май	72,1
Июнь	68,8
Июль	73,2
Август	70,4
Сентябрь	75,9
Октябрь	72,4
Ноябрь	72,7
Декабрь	62,8

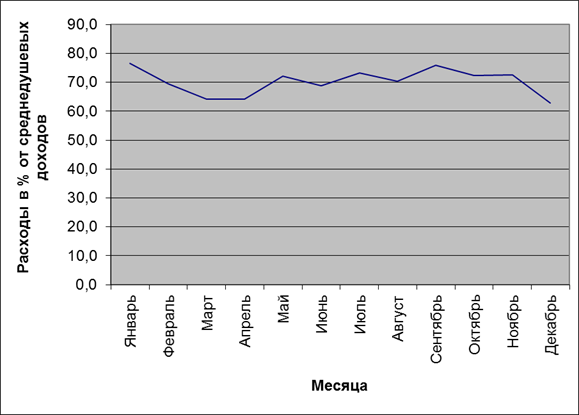
Рисунок 1 - Исходный ряд динамики

Алгоритм моделирования заключается в следующем.

1. Определяется тренд, наилучшим образом аппроксимирующий фактические данные. (Выравниваем исходный ряд с помощью простой скользящей средней, результаты выравнивания приведены в таблице 2).

2. Вычитая из фактических уровней ряда значения сглаженных уровней, получим временной ряд, уровни которого x_ti отражают влияние сезонности и случайных факторов, а их сумма должна быть равна нулю (таблица 2 колонка 6). При этом

Таблица 2 - Сглаживание исходного временного ряда

Квартал	Месяц	Номер компоненты	Расходы в % от общего дохода,	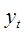Скользящая средняя,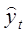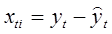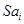
	Январь		76,6		-	-0,585
Февраль		69,6	70,3	-0,7	1,215
Март		64,3	69,7	-5,4	-0,615
	Апрель		64,3	69,7	-5,4	-0,585
Май		72,1	70,3	1,8	1,215
Июнь		68,8	70,3	-1,5	-0,615
	Июль		73,2	70,9	2,3	-0,585
Август		70,4	71,2	-0,8	1,215
Сентябрь		75,9	70,8	5,1	-0,615
	Октябрь		72,4	71,0	1,4	-0,585
Ноябрь		72,7	69,3	3,4	1,215
Декабрь		62,8			-0,615

Для определения S_aiсоставим вспомогательную таблицу 3.

Таблица 3 - К расчету сезонной компоненты

Номер компоненты	Квартал 1	Квартал 2	Квартал 3	Квартал 4	Средняя оценка сезонной компоненты	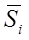Скорректированная сезонная компонента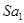
	-	-5,4	2,3	1,4	-0,57	-0,585
	-0,7	1,8	-0,8	3,4	1,23	1,215
	-5,4	-1,5	5,1	-	-0,60	-0,615
Итого					0,06	≈ 0

Если бы сумма средних оценок сезонной компоненты равнялась нулю ( 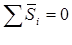), то можно считать значения 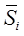окончательными значениями сезонных компонент, т.е., .

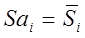Поскольку условие равенства нулю суммы всех сезонных компонент не выполняется, то необходимо произвести корректировку значений сезонных компонент путем вычитания из средней оценки величины, равной отношению суммы средних оценок сезонных компонент к их общему числу

.

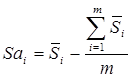Так, в частности, для первой компоненты будем иметь

.

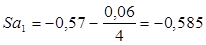Поступая аналогично, заполняем последнюю колонку таблицы 3.

Окончательно значения сезонной компоненты приведены в таблице 2 (колонка 7).

3.Вычитая значения сезонной компоненты из исходных уровней ряда, определяем данные Т+ Е = у_t –Sa_i , которые содержат только тенденцию и случайную компоненту. Результаты расчетов заносим в таблицу 4 (колонка 4).

4. С помощью табличного процессора MS Excel и его инструмента «Добавить линию тренда» формируем аналитическое выражение тенденции. Наилучшим приближением является полином третьего порядка

.

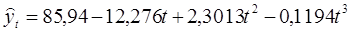Подставляя в данное уравнение значения t =1,…, 12, определяем уровни T для каждого момента времени, заполняем таблицу 4 ( колонка 5).

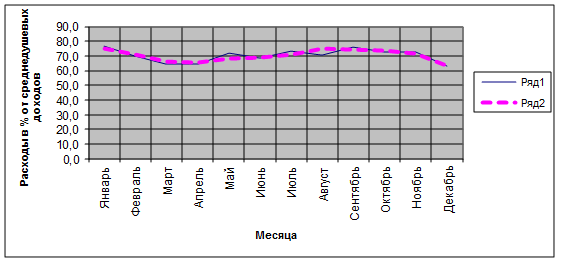
5. С использованием полученного уравнения тенденции определяем смоделированные параметры исследуемого ряда динамики и заполняем колонку 6 таблицы 4. Результаты моделирования показаны на рисунке 2., где ряд 1 – исходные данные,а ряд 2 - результаты моделирования.

Таблица 4- Расчет выровненных значений T и случайных ошибок E в аддитивной модели

ti	yt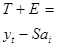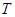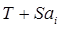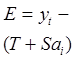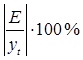
	76,6	-0,585	77,185	75,846	75,261	1,339	1,7
	69,6	1,215	68,385	69,638	70,853	-1,253	1,8
	64,3	-0,615	64,915	66,600	65,985	-1,685	2,6
	64,3	-0,585	64,885	66,015	65,430	-1,130	1,8
	72,1	1,215	70,885	67,168	68,383	3,718	5,2
	68,8	-0,615	69,415	69,340	68,725	0,075	0,1
	73,2	-0,585	73,785	71,818	71,233	1,968	2,7
	70,4	1,215	69,185	73,882	75,097	-4,697	6,7
	75,9	-0,615	76,515	74,819	74,204	1,696	2,2
	72,4	-0,585	72,985	73,910	73,325	-0,925	1,3
	72,7	1,215	71,485	70,440	71,655	1,045	1,4
	62,8	-0,615	63,415	63,692	63,077	-0,277	0,4

6. Определяем абсолютную и относительную ошибки сформированной математической модели временного ряда. (таблица 4, колонки 7, 8). Анализ величины относительной ошибки, которая не превышает 7% , свидетельствует о достаточной точности теоретического моделирования и о возможности использовать модель для краткосрочного прогнозирования расходов населения.