Сложная и большая система

Основы системного анализа

Раздел 1. Введение

1. Системность как всеобщее свойство материи.

1.1. Определение системы.

1.2. Сложная и большая система.

1.3. Классификация систем по их основным свойствам.

1.4. Искусственная система как средство достижения цели.

1.5. Системность как всеобщее свойство материи

1.6. Системность познавательных процессов

1.7. Методология системного подхода

1.8. Развитие системных представлений в науке и практике

1.9. Контрольные вопросы и упражнения

Раздел 2. Имитационное моделирование как метод исследования систем большой сложности

2.1. Введение

2.2. Основные понятия

2.3. Принципы и методы построения имитационных моделей

2.4. Вопросы для самопроверки

2.5. Упражнения

2.6. Случайные события и их имитация

2.7. Имитация случайного события

2.8. Имитация сложного события

2.9. Имитация сложного события, состоящего из зависимых событий

2.10. Имитация событий, составляющих полную группу

2.11. Вопросы для самопроверки

2.12. Упражнения

2.13. Имитация непрерывных случайных величин

2.14. Метод обратной функции

2.15. Метод фон Неймана (режекции)

2.16. Алгоритм получения значений нормально распределенной случайной величины

2.17. Алгоритм получения случайной величины, распределенной по Пуассону

2.18. Упражнения

2.19. Алгоритмы получения значений систем случайных величин (случайных векторов)

2.20. Метод аналитических преобразований

2.21. Метод разложения по координатным случайным величинам

2.22. Алгоритм получения значений системы дискретных случайных величин

2.23. Упражнения

2.24. Имитация случайных процессов

2.25. Имитация нестационарных случайных процессов

2.26. Имитация стационарных СП

2.27. Имитация стационарных нормальных СП

2.28. Обработка результатов моделирования

2.29. Оценка вероятности

2.30. Гистограмма

2.31. Оценка математического ожидания

2.32. Оценка дисперсии

2.33. Оценка корреляционного момента

2.34. Оценка характеристик случайного процесса

2.35. Количество реализаций, обеспечивающих заданную точность

Раздел 3. Основы теории систем массового обслуживания

3.1. Введение

3.1.1. Историческая справка

3.1.2. Примеры систем массового обслуживания. Анализ задач ТСМО

3.1.3. Понятия, определения, терминология

3.1.4. Классификация СМО

3.1.5.Основная задача ТСМО

3.2. Математические модели потоков событий

3.2.1. Регулярный и случайный потоки

3.2.2. Простейший пуассоновский поток

3.2.3. Свойства простейшего пуассоновского потока

3.2.4. Простейший поток и решение практических задач

3.2.5. Нестационарные пуассоновские потоки

3.2.6. Потоки с ограниченным последствием (потоки Пальма)

3.2.7. Потоки восстановления

Термины и определения

Литература

Введение

Формирование системного анализа в качестве самостоятельного исследовательского направления обусловлено общей тенденций развития человечества, которая сложилась к настоящему времени. Эта тенденция проявляется: во все более глубоком рациональном вмешательстве в организационную деятельность человека, а также в процессы выработки и принятия им решений.

В 70-х гг. ХХ столетия в научной литературе появилась масса терминов: “системная революция”, “системный подход”, “общая теория систем”, “системный анализ операций” и т.д. Это говорило об объединении усилий специалистов различных профессий для решения общих задач, связанных с изучением, проектированием и управлением сложными системами. Причем, начиная с этого времени понятие системности стало не только теоретической категорией, но осознанной необходимостью в практической деятельности. Именно это “системное движение” [16], привело к интеграции отдельных научных направлений по созданию науки, получившей название “системный анализ”,которая в настоящее время выступает как самостоятельная дисциплина.

Предметом изучения системного анализа является система, независимо от ее природы, организации, способа существования и способа описания.

Целью рассмотрения системы является решение задач анализа, управления и проектирования.

В ходе рассмотрения реальной системы приходится сталкиваться с совокупностью проблем, решение которых могут быть под силу только коллективу профессионалов различного профиля. К таким проблемам относятся проблемы начиная с выделения системы из среды, ее формального описания, взаимодействия с внешней средой, выбора или разработки оптимального алгоритма управления, оптимального проектирования, технических средств управления и т.п., кончая подбором кадров и организацией коллектива по решению этих работ. Для решения названных проблем системный анализ привлекает широкий спектр различных наук и различные сферы практической деятельности. При этом он придает большое значение методическим аспектам любого системного исследования [1, 4,11, 15, 16].

Данный курс лекций посвящен решению локальной задачи системного анализа – вопросам методологии системных исследований и математическим методам этих исследований.

Системность как всеобщее свойство матери

Определение системы

Центральным понятием системного анализа является понятие “система”.

Определение:

o система есть совокупность элементов (подсистем). При определенных условиях элементы сами могут рассматриваться как системы, а исследуемая система – как элемент более сложной системы:

o связи между элементами в системе превосходят по силе связи этих элементов с элементами, не входящими в систему. Это свойство позволяет выделить систему из среды;

o для любой системы характерно существование интегративныхкачеств (свойство эмерджентности), которые присущи системе в целом, но не свойственны ни одному ее элементу в отдельности: систему нельзя сводить к простой совокупности элементов;

o система всегда имеет цели, для которых она функционирует и существует.

Сложная и большая система

Одной из характерных тенденций развития общества в настоящее время является появление больших чрезвычайно сложных систем (крупные автоматизированные, технологические, энергетические, гидротехнические, информационные и другие комплексы). С другой стороны стремление познать мир обитания человечества как сложную многофункциональную систему стало реальностью сегодняшнего дня. Все это привело к необходимости определить понятие сложной системы, разработать методические принципы ее исследования, управления и проектирования.

В настоящее время однозначного, четкого определения сложной системы нет. Известны различные подходы и предложены различные формальные признаки ее определения. Так, советский ученый Г.Н. Поворов предлагает относить к сложным системы имеющие 10⁴-10⁷ элементов; к ультрасложным - системы, состоящие из 10⁷-10³⁰ элементов; и к суперсистемам – системы из 10³⁰-10²⁰⁰ элементов.

Такой подход имеет тот недостаток, что данное определение сложности является относительным, а не абсолютным.

Английский кибернетик С. Бир предлагает к сложным относить системы, описываемые на языке теоретико-вероятностных методов (мозг, экономика, форма и т.п.) [3].

Наиболее четким на наш взгляд, определением сложных систем является определение, данное, например, в [9].

Определение:

Сложной системой называется система, в модели которой недостаточно информации для эффективного управления этой системой.

Таким образом, признаком простоты системы является достаточность информации для ее управления. Если же результат управления, полученный с помощью модели, будет неожиданным, то такую систему относят к сложной.

Для перевода системы в разряд простой необходимо получение недостающей информации о ней и включение ее в модель.

От сложных систем необходимо отличать большие системы.

Определение:

Система, для актуализации модели которой в целях управления недостает материальных ресурсов (машинного времени, емкости памяти, других материальных средств моделирования) называется большой [9].

К таким системам относятся экономические, организационно-управленческие, нейрофизиологические, биологические и т.п. системы.

Способом перевода больших систем в простые является создание новых более мощных средств вычислительной техники.

Как видно из определений, понятия большой и сложной системы являются разными. Однако в литературе эти понятия определены не однозначно.

Некоторые авторы вообще не используют этих понятий, другие используют их как синонимы, а некоторые считают разницу между ними чисто количественной.

Чтобы еще раз подчеркнуть существенную разницу между понятиями “большая” и “сложная” системы приведем примеры из работы [9 ]. При этом сведем их в следующую таблицу:

Таблица 1.1.

№	Система	Малая	Большая	Простая	Сложная
	Исправный бытовой прибор для пользователя	+		+
	Неисправный бытовой прибор для мастера	+			+
	Шифрозамок для похитителя		+	+
	Мозг, живой организм		+		+

В табл. 1.1. знаком “+” отличены классификационные признаки систем. Поясним, например, почему шифрозамок отнесен к классу больших и простых систем. Эта система – большая, так как у похитителя может не хватить ресурса времени для вскрытия замка; а простая – потому что вскрытие сводится к простому многовариантному перебору шифров. На рис. 1.1. показаны всевозможные сочетания признаков систем «простая – сложная», «малая – большая».

На рис. 1.1. показаны всевозможные сочетания признаков систем «простая – сложная», «малая – большая».

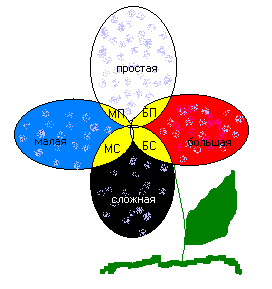
рис. 1.1.