Уравнение кривой в пространстве
Полная производная
Если z = F(x, y, u, v) и y = f (x), u = φ (x), v = ψ (x), то функция z = F(x, f (x), φ (x), ψ (x)) — является функцией одного переменного. В соответствии с (3) в этом случае имеем
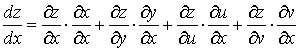 .
.
Учитывая, что переменные y, u, v являются функциями одного переменного, получим окончательно формулу для вычисления полной производной
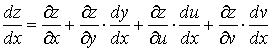 .
.
Полный дифференциал
Если функция z=f(x, y) дифференцируема, то ее полный дифференциал dz равен dz=A∆x+B∆y (1)
Замечая, что A=∂z/∂x, B=∂z/∂y, запишем формулу (1) в следующем виде
dz= ∂z/∂x*Δx+∂z/∂y*Δy
Распространим понятие дифференциала функции на независимые переменные, положив
дифференциалы независимых переменных равными их приращениям: dx=∆x; dy=∆y.
После этого формула полного дифференциала функции примет вид
dz= ∂z/∂x*dx+∂z/∂y*dy
5.Производная от функции двух переменных, заданной неявно.
F(x,y)=0 (1)
Пусть функция у от х задана в неявном виде с помощью уравнения (1)
F(x,y); Fx’(x,y);Fy’(x,y)=D
(x,y)
Сама функция и ее частное производное являются непрерывными функции в некоторой области D содержащей точку М(х,у), координаты котрой удовлетворяют уравнению (1). Предполагается что в этой точке Fy’(x,y)≠0
Yx’=- 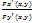
6) Производная от функции трех переменных заданных неявно.
Пусть функция задана в неявном виде с помощью уравнения F(x,y,z)=0. Если паре значений x и у из области D соответствует одно или несколько значений z , удовлетворяющих данному уравнению, то это уравнение неявно определяет одну или несколько функций z от x или y.
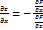 ;
; 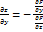
7) Частные производные различных порядков от функции нескольких переменных.
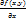 ;
;
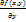 ; - эти функции могут иметь частные производные второго порядка и определяются они так
; - эти функции могут иметь частные производные второго порядка и определяются они так
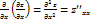 ;
;
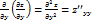 ;
;
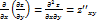 ;
;
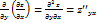 ;
;
8) Теорема о независимости результата дифференцирования функции нескольких переменных от порядка дифференцирования (доказательства в конспекте нет, но он вроде и не требовал)
Частные производные взятые по различным переменным называются смешанными частными производными. Если частные производные высшего непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования равны между собой.
9) Необходимые и достаточные условия экстремума функции нескольких переменных.
Необходимые условия:
Если функция z=f(x,y) имеет в точке М(Xo,Yo) экстремум, то каждая частная производная первого порядка от Z обращается в ноль при этих значениях аргумента (Xo и Yo) или не существует.
Достаточные условия:
Пусть в некоторой точке с координатой Xo и Yo эта функция имеет непрерывные частные производные до 3 порядка включительно и точка М с координатами (Xo,Yo) является стационарной.
Тогда при X=Xo, Y=Yo:
1) Δ= 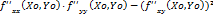
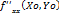 - A
- A
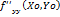 – C
– C
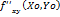 – B
– B
F(x,y)=max, если 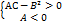
2) F(x,y)=min, если 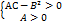
3) 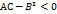 – не max и не min.
– не max и не min.
4) 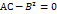 - экстремум может быть или не быть, требуется проведение доп. Исследований.
- экстремум может быть или не быть, требуется проведение доп. Исследований.
10) Условный экстремум функции нескольких переменных.
Условным экстремумом функции z=f(x,y) называется экстремум этой функции, достигнутый при условии, что переменные x и y связаны между собой уравнением связи переменных. Описание условного экстремума можно свести к исследованию на обычный экстремум так называемой функции Лагранжа – U=f(x,y)+λϕ(x,y), где λ – неопределенный постоянный множитель, тогда необходимое условие экстремума функции Лагранжа будет иметь следующий вид.
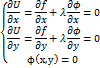
уравнение кривой в пространстве
Кривая в обычном пространстве, не лежащая на плоскости, называется пространственной кривой. Чтобы исследовать дифференциальную геометрию такой кривой, зададим ее параметрическими уравнениями x = f(s), y = g(s), z = k(s) (s – натуральный параметр) или, в векторной форме, уравнением X = F(s). Единичный вектор касательной определяется равенством

Вектор dT/ds в каждой точке задает нормаль к кривой; заметим, что это лишь одна из бесконечного множества нормалей к пространственной кривой в этой точке. Единичный вектор в направлении вектора dT/ds называется единичным вектором главной нормали N кривой, а длина вектора dT/ds, как и в случае плоских кривых, называется кривизной кривой:

Вектор dN/ds перпендикулярен к N, и поэтому его можно записать в виде

где B – единичный вектор нормали, перпендикулярной к N. Прямая, определяемая вектором B, называется бинормалью к кривой, а коэффициент t в (6) – кручением кривой. Наконец, рассмотрим вектор dB/ds; можно показать, что

Соотношения (5)–(7) называются формулами Френе. Из них следует, что если функции k = f (s) и t = y (s) заданы, то кривая определена однозначно с точностью до положения в пространстве. Таким образом, в этих формулах содержится вся теория пространственных кривых. Плоскость, определяемая векторами T и N, называется соприкасающейся, плоскость, содержащая векторы N и B, – нормальной и плоскость, проходящая через векторы B и T, – спрямляющей.
