Формулирование общей задачи линейного программирования
В.П. Сухинин, М.В. Горшенина
ПРОИЗВОДСТВЕННЫЙ МЕнеджмент
Методические указания к практическому занятию:
«Построение линейных математических моделей
Экономических задач»
Сызрань 2011
 УДК 658
УДК 658
Методические указания к выполнению практической работы/В.П. Сухинин, М.В. Горшенина; Самар. гос. техн. ун-т., филиал в г. Сызрани. Сызрань, 2011.10 с.
| |
Данные методические указания адресованы студентам, обучающимся по специальности 080502 – Экономика и управление на предприятии.
| |
Построение линейных математических
Моделей экономических задач
Цель работы: формирование навыков построения математических моделей одноиндексных задач линейного программирования
Формулирование общей задачи линейного программирования
В практической деятельности организаций бизнеса наиболее часто приходится решать задачи, связанные с распределением ресурсов (труда, сырья, материалов, оборудования, денежных средств). Обычно размеры ресурсов ограничены, поэтому возникает необходимость оптимального использования имеющихся ресурсов для достижения определенной цели управления. Например, если фирма выпускает несколько видов продукции с использованием одного и того же оборудования и трудовых ресурсов, то нужно решить, какое количество продукции каждого вида производить, чтобы получить наибольшую прибыль, или максимизировать время использования оборудования, или минимизировать затраты труда и т.д.
Для решения таких задач используются методы линейного программирования. В задаче линейного программирования целевая функция F(X) и ограничения задаются линейными неравенствами. Требуется найти значение переменных X1, X2,…,Xn при которых линейная форма
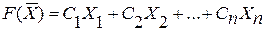 (1)
(1)
имеет максимум (минимум) при условиях:
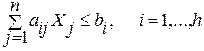 (2)
(2)
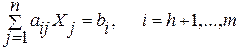 (3)
(3)
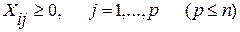 (4)
(4)
Соотношения (2,3) называются функциональными, (4) – прямыми.
Для постановки задачи линейного программирования необходимо:
1) определить переменные, значения которых нужно получить;
2) установить цели и выразить целевую функцию через переменные;
3) определить ограничения на ресурсы и представить их через переменные.
Пример 1
Металлургическому заводу требуется уголь с содержанием фосфора не более 0,03% и с долей зольных примесей не более 3,25%. Завод закупает три сорта угля А, В, С с известным содержанием примесей (табл. 1).
В какой пропорции следует смешивать исходные продукты АВС, чтобы смесь удовлетворяла ограничениям на содержание примесей и имела минимальную цену?
Решение:
Таблица 1
| Сорт угля | Содержание примесей, % | Цена за 1 тонну, руб. | |
| фосфор | зола | ||
| А В С | 0,06 0,04 0,02 | 2,0 4,0 3,0 |
Строим математическую модель:
Х1 – количество угля сорта А в тонне смеси,
Х2 - количество угля сорта В в тонне смеси,
Х3 - количество угля сорта С в тонне смеси.
Тогда целевая функция примет вид:
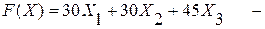
это стоимость одной тонны смеси. Ограничение на содержание фосфора:
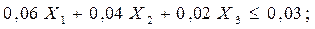
ограничение на содержание зольных примесей:
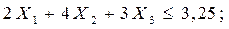
ограничение на состав тонны смеси:
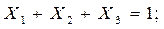
Важным моментом проверки правильности составления ограничений является проверка совпадения единиц измерения левой и правой частей ограничения (% =%).
Окончательно математическая модель примет вид:
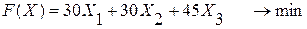
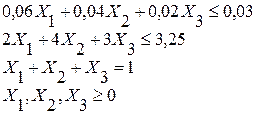
Пример 2
Фирма выпускает три вида продукции. В процессе производства используются три технологические операции. На рис. 1 изображена схема производства изделий трех видов.
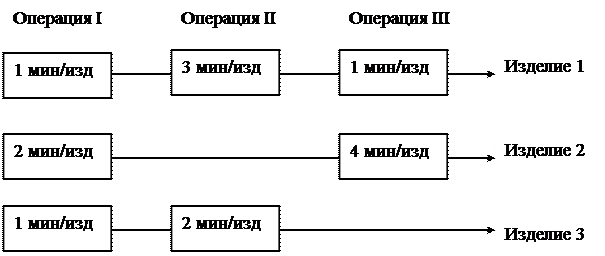 |
Р и с. 1. Схема производства изделий
В прямоугольниках указана длительность технологической операции при изготовлении одного изделия каждого вида. Данные технологические операции могут использоваться фирмой и для других производственных целей, поэтому существуют ограничения по использованию фонда рабочего времени в сутки:
для операции I – 430 мин;
для операции II – 460 мин;
для операции III – 420 мин.
Ожидаемая прибыль от продажи изделий составляет 3, 2 и 5 руб. соответственно.
Каков наиболее выгодный суточный объем производства каждого изделия?
Решение:
Пусть Х1 – количество изделий первого вида,
Х2 – количество изделий второго вида,
Х3 – количество изделий третьего вида.
Тогда математическая формулировка задачи примет следующий вид:
целевая функция (величина прибыли за сутки):
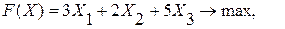
при ограничениях (предельное время использования операций в течение суток):
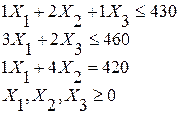 | - для операции 1 - для операции 2 - для операции 3 |
Контрольные вопросы
1. Что такое математическое и линейное программирование?
2. Какова общая форма записи модели линейного программирования?
3. Что такое допустимое и оптимальное решения?
4. Каковы основные этапы построения математической модели линейного программирования?
5. Каков экономический смысл и математический вид целевой функции?
6. Объясните способ построения ограничения задачи.
Литература
1. Ильенкова С.Д. Производственный менеджмент [Текст]/ С.Д. Ильенкова – М.: ЮНИТИ-ДАНА, 2000.
2. Орлов И.А. Менеджмент [Текст]/ И.А. Орлов – М.: Изумруд, 2003.
3. Зайцев М.Г. Методы оптимизации управления и принятия решений: примеры, задачи, кейсы [Текст]/ М.Г. Зайцев - М.: Дело, 2008.
