Задача для самолстоятельного выполнения

ЛАБОРАТОРНАЯ РАБОТА №7

ПАУТИНООБРАЗНАЯ МОДЕЛЬ.

РАСЧЕТ ТРАЕКТОРИИ ИЗМЕНЕНИЯ ЦЕНЫ, СПРОСА И ПРЕДЛОЖЕНИЯ С ПОМОЩЬЮ Microsoft Excel

ЦЕЛЬ РАБОТЫ

Изучение механизма построения паутинообразной модели, реализации процесса поиска равновесной цены в табличном редакторе Microsoft Excel.

ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Выполнение лабораторной работы включает следующие этапы:

1) изучить теоретическую часть работы;

2) построить математическую модель;

3) исследовать модель с помощью Microsoft Excel;

4) подготовить письменный отчет;

5) защитить лабораторную работу.

ОСНОВНЫЕ СВЕДЕНИЯ

Построение паутинообразной модели основано на предположении о том, что спрос и предложение являются функциями от цены.

Введем обозначения:

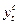- спрос в момент времени t;

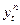- предложение в момент времени t;

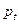- цена в момент времени t.

Спрос в данный момент зависит от цены в этот же момент времени:

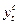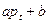= , (1)

а предложение – от цены в предшествующий момент времени:

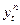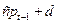= (2)

так как присутствует запаздывание в реакции производства на изменение цены.

Обычно с увеличением цены спрос падает, а предложение возрастает .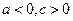

Равенство в каждый момент времени спроса и предложения 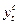= 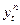, (3)

Завершает описание паутинообразной модели.

Из соотношения (3) получим модель для цены в виде:

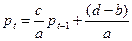, (4).

Значение цены, при котором устанавливается равенство спроса и предложения и которое не приводит к дальнейшим изменениям их, обозначим через 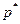. Это равновесная цена

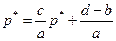, (5)

откуда получаем ее значение:

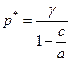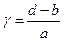, где . (6)

Исследование процесса, описываемого моделью, на сходимость дает основание утверждать:

1. Если 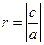<1, то при ;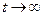

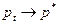2. Если 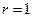, то при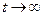 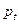колеблется около равновесного значения;

3. Если 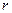>1, то при 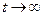цена будет отклоняться на все большую величину от ее равновесного значения.

По данным таблицы 1 рассчитаем траектории изменения цены, спроса и предложения и построим график движения цены к равновесному состоянию.

Таблица 1

№	цена	спрос	предложение
	7,5	23,25	10,13
	15,38	19,32	12,87
	19,25	17,39	14,24
	21,12	16,44	14,9
	24,21	14,9	15,98
	25,53	14,24	16,44
	28,25	12,89	17,39
	33,75	10,13	19,32

Порядок выполнения задания

1. Введем исходные данные (рис.1)

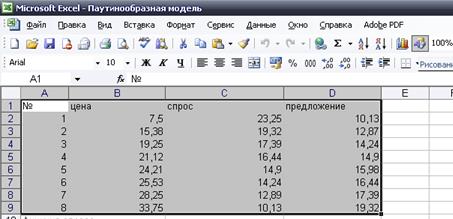
Рисунок 1 – Ввод исходных данных

2. Оценим параметры регрессионной зависимости спроса от цены с помощью пакета Анализ данных (рис.2).

Рис. 2 Запуск поката «Анализ данных - Регрессия»

Заполнение диалогового окна для получения функции спроса (рис.3)

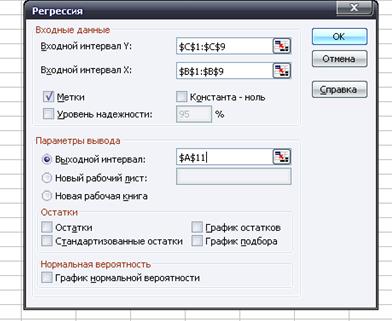
Рисунок 3 – Заполнение диалогового окна

Результаты работы (рис.4)

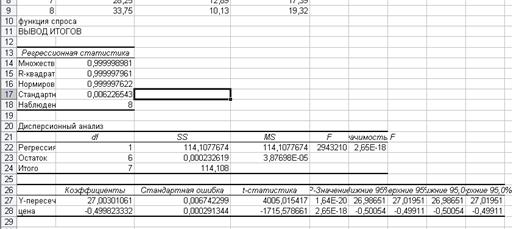
Рисунок 4 – Вывод результатов работы пакета «Анализ данных - Регрессия»

Итак, получили уравнение 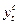= 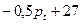(7)

3. Оценим параметры регрессионной зависимости предложения от цены.

Заполнение диалогового окна для получения функции предложения (рис.5)

Функция предложения

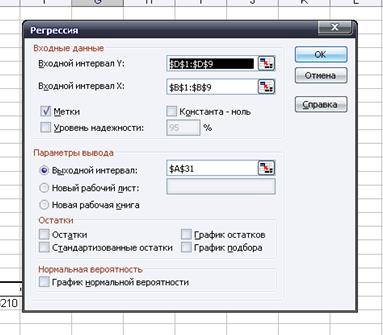
Рисунок 5 – Заполнение диалогового окна

Результаты работы (рис.6)

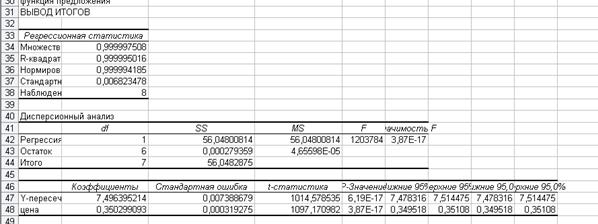
Рисунок 6 – Вывод результатов работы пакета «Анализ данных - Регрессия»

Итак, получили функцию 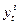= 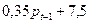(8)

4. Запишем условия равновесия спроса и предложения:

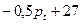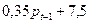= (9)

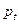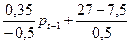Или = (10)

5. Рассчитаем траекторию изменения цены, спроса и предложения:

а) на свободное поле рабочего листа Excel (например, в ячейки А51 и А52) дважды введем значение первоначальной цены 7,5;

б) в ячейку А53 введем формулу (10) (рис.7)

Рисунок 7 - Ввод формулы 10 в ячейку А53

Введем формулу 10 в ячейку А54 (рис.8)

Рисунок 8 – Ввод формулы 10 в ячейку А54

Скопируем формулу в блок А55…А66;

в) в ячейку В51 введем формулу (7) и скопируем ее в блок В52…В66;

г) в ячейку С51 введем формулу (8) и скопируем ее в блок С52…С66;

д) в ячейки Д51 и Д52 введем соответственно формулы (7) и (8) и последнюю из них скопируем в блок Д53…Д66.

В результате этих действий получим таблицу 2

Таблица 2

цена	траектория спроса	траектория предложения	траектория движения к равновесной цене
7,500	23,250	10,125	23,250
7,500	23,250	10,125	10,125
33,750	10,125	19,313	10,125
33,750	10,125	19,313	19,313
15,375	19,313	12,881	19,313
15,375	19,313	12,881	12,881
28,238	12,881	17,383	12,881
28,238	12,881	17,383	17,383
19,234	17,383	14,232	17,383
19,234	17,383	14,232	14,232
25,536	14,232	16,438	14,232
25,536	14,232	16,438	16,438
21,125	16,438	14,894	16,438
21,125	16,438	14,894	14,894
24,213	14,894	15,974	14,894
24,213	14,894	15,974	15,974

6. По данным, описывающим траекторию цены, спроса и предложения, построим график типа ХУ (точечный график), назначив Х блок А51…А66, У1 – блок В51…В66, У2 – блок С51…С66, У3 – блок Д51…Д66.

Построенный график имеет вид (рис.9):

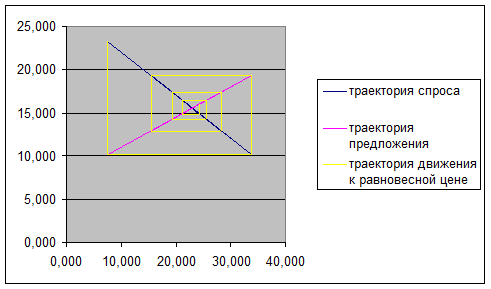
Рисунок 9 – График

ЗАДАЧА ДЛЯ САМОЛСТОЯТЕЛЬНОГО ВЫПОЛНЕНИЯ

По данным таблицы 3 построить уравнение предложения и уравнение цены. Используя параметры этих уравнений, вычислить параметры уравнения спроса. Определить равновесную цену. С помощью построенных уравнений сгенерировать наборы данных и построить график траектории поиска равновесной цены.

Таблица 3

№	цена в момент t	цена в момент времени t-1	предложение
	-		6,74
	22,52	22,52	12,87
	10,25	10,25	8,58
	18,84	18,84	11,58
	12,83	12,83	9,48
	17,04	17,04	10,95
	14,09	14,09	9,92
	16,15	16,15	10,64