Простейшая математическая модель эпидемии
За многие годы существования человечества огромное число людей погибло от различных эпидемий. Чума, холера, грипп и др. нередко поражали значительные массы людей. Для того, чтобы иметь возможность бороться с эпидемиями, т.е. своевременно применять те или иные медицинские мероприятия (карантины, вакцинации и т.п.),необходимо уметь сравнивать эффективность этих мероприятий. Сравнить же их можно лишь в том случае, если есть возможность предсказать, как при том или ином мероприятии будет меняться ход эпидемии, т.е. как будет меняться число заболевших.
Отсюда возникает необходимость в построении модели, которая могла бы служить целям прогноза.
Для простоты рассмотрим естественный ход эпидемии без какого-либо вмешательства и попробуем спрогнозировать последствия.
Так как нашей целью является лишь создание иллюстративной модели, то здесь мы абстрагируемся от очень многих факторов ( условия размножения бактериальных клеток, степень восприимчивости к инфекции отдельных людей, вероятность встречи носителя инфекции со здоровым человеком и т.д.)
Итак, пусть имеется N здоровых людей, и в момент времени t=0 в эту группу попадает один заболевший человек – источник инфекции. Будем предполагать, что никакого удаления заболевших из группы не происходит. Считаем также, что человек становится источником инфекции сразу же после того, как он сам заразится.
Допустим в некоторый момент времени t
X(t) – число источников инфекции,
Y(t) – число людей, могущих заболеть,
Тогда имеем X(t)+Y(t)=N+1 в любой момент времени.
При t=0 выполняется условие X(0)=1
Количество новых больных dX, появившихся за промежуток времени dt, будет пропорционально числу встреч здоровых и заболевших людей, т.е. произведению величин XY. Следовательно, можно записать
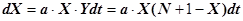 или
или 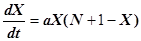 ,
,
где a – коэффициент пропорциональности.
Полученное дифференциальное уравнение вместе с условием X(0)=1 определяет функцию X(t), т.е. численность заболевших в момент времени t.
Найдем общее решение, предварительно разделив переменные.
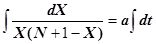
Чтобы взять первый интеграл, разделим числитель и знаменатель дроби на 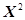 и введем новую переменную
и введем новую переменную 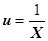 , тогда
, тогда 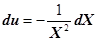 , и отсюда
, и отсюда 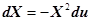 .
.
Заменим под интегралом переменную, получим
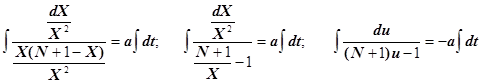
После интегрирования имеем
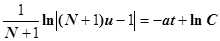 , и, следовательно
, и, следовательно 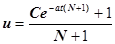
С учетом того, что 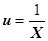 ,получим искомую функцию X(t)
,получим искомую функцию X(t)
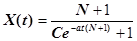
Так как при t=0 значение X(t)=1, то для определения величины С имеем уравнение
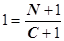 , откуда C=N
, откуда C=N
Окончательно получаем
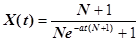
Итак, мы знаем число заболевших как функцию времени. Проанализируем полученную формулу. При возрастании t знаменатель дроби убывает, т. е. X(t) увеличивается. Это соответствует нашим представлениям, так как, согласно им, число заболевших может только увеличиваться.
Интересно выяснить, как меняется скорость увеличения числа больных. Для решения этого вопроса нужно изучить величину 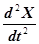 .
.
Дифференцируя, получаем
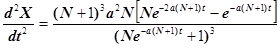
Числитель дроби обращается в нуль при 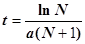 .
.
Таким образом, когда 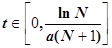 , величина
, величина 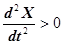 , а когда
, а когда 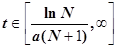 , величина
, величина 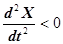 .
.
Следовательно, функция 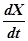 - скорость возрастания числа заболевших – растет вплоть до момента
- скорость возрастания числа заболевших – растет вплоть до момента 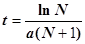 , а затем убывает.
, а затем убывает.
Этот результат хорошо согласуется с экспериментальными данными, так как известно, что в начале эпидемии число заболевших резко растет, а впоследствии скорость распространения инфекции снижается.
