И все-таки, для чего нам необходимо знать положение главных центральных осей, а также значения главных центральных моментов инерции поперечного сечения стержня?

Их определение, как это не покажется уважаемому Читателю неожиданным, напрямую связано именно с обеспечением прочности, жесткости и устойчивости стержня (то есть, с теми основными вопросами, которые и изучаются в сопротивлении материалов), но при более сложных, чем центральное растяжение (сжатие) и сдвиг, видах деформации. Подробнее об этих видах деформации мы будем говорить в наших последующих беседах, а сейчас все-таки попытаемся ответить, хотя бы в общих чертах, на поставленный вопрос.

Рассмотрим следующий пример. Предположим, что нам необходимо заделать одним концом в стену обычную ученическую линейку, поперечное сечение которой представляет собой прямоугольник, у которого один размер (высота) намного больше другого размера (толщины). Предполагается, что на другом конце к этой линейке будет приложена вертикальная сила P.

Как нам следует расположить линейку в пространстве по отношению к этой нагрузке, чтобы напряжения в ней и прогиб свободного конца были минимальными? Ответ на этот вопрос очевиден – «ребром». То есть таким образом, чтобы силовая плоскость (плоскость, в которой расположена внешняя нагрузка) была перпендикулярна к оси максимум поперечного сечения линейки. Правда, при этом нам необходимо помнить о том, что с ростом силы P линейка попытается «выскользнуть» из-под нагрузки. И в этом легко убедиться, выполнив соответствующий эксперимент. При некотором значении нагрузки 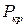, называемой критической, линейка внезапно изогнется вбок с одновременным закручиванием. Это явление, которое называется потерей устойчивости плоской формы изгиба, вряд ли произойдет с линейкой, расположенной «плашмя». Очевидно, что расположенная таким образом линейка скорее сломается, чем потеряет устойчивость.

А как нам расположить под вертикальной сосредоточенной силой стержень, поперечное сечение которого представляет собой, например, швеллер с приваренным к его полке неравнобоким уголком? Ответ на этот вопрос следующий: и в этом случае, с точки зрения прочности и жесткости, стержень нужно расположить так, чтобы силовая плоскость была перпендикулярна к оси максимум данного поперечного сечения.

В заключение этой беседы отметим, довольно часто говорят просто главные оси инерции и главные моменты инерции, подразумевая, что эти понятия имеют отношения к центру тяжести поперечного сечения стержня.

КРУЧЕНИЕ

В этой беседе нам предстоит познакомиться с основами теории кручения, причем кручения только стержней круглого поперечного сечения. Круглый стержень, испытывающий деформацию кручения, принято называть валом. Кручение элементов конструкции и деталей машин встречается очень часто. Одним из наиболее характерных случаев является кручение вала машины. На кручение работают оси локомотивов, стержень винтовой цилиндрической пружины и т. д.

5.1. Какой вид деформации стержня называется кручением?

Мысленно заделаем, например, левый конец стержня круглого поперечного сечения в стену и приложим к его правому свободному концу внешний момент, вращающий относительно оси стержня z. Этот внешний момент мы будем называтьскручивающим моментоми обозначать его 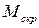. Такая внешняя нагрузка вызовет в стержне деформацию кручения, которая характеризуется тем, что одно поперечное сечение поворачивается на некоторый угол относительно другого сечения. Если угол поворота мал, то можно предположить, что расстояние между этими сечениями останется прежним. В поперечных сечениях стержня, при такой деформации, возникнет только одно внутреннее усилие – крутящий момент, который мы будем обозначать .

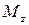Угол, на который повернется нагруженное крайнее правое поперечное сечение стержня относительно неподвижного левого сечения, называется углом закручивания стержня и обозначается буквой .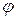

5.2. Как строится эпюра крутящих моментов?

Крутящий момент, возникающий в поперечном сечении стержня, определяется методом сечений. Как уже отмечалось в первой беседе, он равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня (иными словами, действующих по одну сторону от рассматриваемого сечения стержня). Эпюра крутящих моментов представляет собой график, показывающий изменение крутящего момента по длине вала 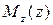. При построении эпюры крутящих моментов обычно используется следующее правило знаков:

Если при взгляде на поперечное сечение стержня мы видим, что внешний скручивающий момент вращает рассматриваемую часть стержня против хода часовой стрелки, то он вызывает в этом сечении положительный крутящий момент, который, в свою очередь, противодействуя этому скручивающему моменту, будет направлен по ходу часовой стрелки.