Проверка существенности факторов и показатели качества регрессии

Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации.

Оценка тесноты связи

Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат.

Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

. (1.44)

Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции:

.

Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

. (1.45)

Можно пользоваться следующей формулой индекса множественной детерминации:

. (1.46)

При линейной зависимости признаков формула индекса множественной корреляции может быть представлена следующим выражением:

, (1.47)

где – стандартизованные коэффициенты регрессии; – парные коэффициенты корреляции результата с каждым фактором.

Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции.

Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:

, (1.48)

где

– определитель матрицы парных коэффициентов корреляции;

– определитель матрицы межфакторной корреляции.

В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений 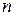. Если число параметров при 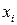равно 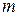и приближается к объему наблюдений, то остаточная дисперсия будет близка к нулю и коэффициент (индекс) корреляции приблизится к единице даже при слабой связи факторов с результатом. Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции.

Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов делится на число степеней свободы остаточной вариации , а общая сумма квадратов отклонений на число степеней свободы в целом по совокупности .

Формула скорректированного индекса множественной детерминации имеет вид:

, (1.49)

где 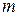– число параметров при переменных 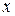; 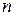– число наблюдений.

Поскольку , то величину скорректированного индекса детерминации можно представить в виде:

. (1.49а)

Чем больше величина 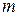, тем сильнее различия и .

Как было показано выше, ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии ( -коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей). Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции.

Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии.

Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель.

В общем виде при наличии 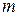факторов для уравнения

коэффициент частной корреляции, измеряющий влияние на 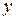фактора 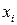, при неизменном уровне других факторов, можно определить по формуле:

, (1.50)

где – множественный коэффициент детерминации всех 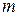факторов с результатом; – тот же показатель детерминации, но без введения в модель фактора .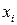

При двух факторах формула (1.41) примет вид:

; . (1.50а)

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, – коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:

. (1.51)

При двух факторах данная формула примет вид:

; . (1.51а)

Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению возможно исчисление трех частных коэффициентов корреляции второго порядка:

, , ,

каждый из которых определяется по рекуррентной формуле. Например, при имеем формулу для расчета :

. (1.52)

Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии следует, что , т.е. no силе влияния на результат порядок факторов таков: , , , то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, .

Из приведенных выше формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле:

.(1.53)

В частности, для двухфакторного уравнения формула (1.44) принимает вид:

. (1.54)

При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице. Из единицы вычитается доля остаточной вариации результативного признака , обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.