Трансфинитная индукция
Комментарий. Метод математической индукции. Применяется для высказываний 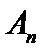 , зависящих от натурального параметра
, зависящих от натурального параметра 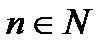 . Докажем, что утверждение
. Докажем, что утверждение 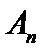 справедливо
справедливо 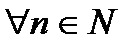 , если: 1) Утверждение
, если: 1) Утверждение 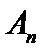 справедливо при
справедливо при 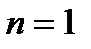 и 2) из справедливости
и 2) из справедливости 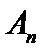 для произвольного
для произвольного 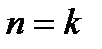 следует справедливость его для
следует справедливость его для 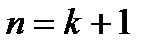 .
.
■. 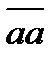 . Пусть утверждения 1 и 2 выполняются, но
. Пусть утверждения 1 и 2 выполняются, но 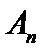 справедливо не для всех
справедливо не для всех 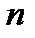 . Так как,
. Так как, 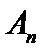 справедливо при
справедливо при 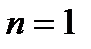 (утверждение 1), то существует такое
(утверждение 1), то существует такое 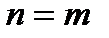 , где
, где 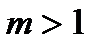 , при котором
, при котором 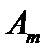 не справедливо, причём
не справедливо, причём 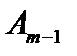 ещё справедливо. Положив
ещё справедливо. Положив 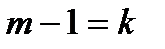 , мы получим противоречие с утверждением 2. ■
, мы получим противоречие с утверждением 2. ■
Для применения метода математической индукции следует сделать следующие операции:
1. Ставится «математический эксперимент», и получают 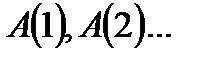 .
.
2. Делается предположение о виде формулы 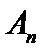 . Оно называется “dicto simplisister”, то есть “сказано простаком”.
. Оно называется “dicto simplisister”, то есть “сказано простаком”.
3. Проверяется утверждение 1 (фактически на первом этапе).
4. Доказывается утверждение 2.
Для натуральных чисел доказательство принципа математической индукции опирается на то, что любое непустое подмножество натуральных чисел имеет наименьший элемент. Если это свойство выполняется для произвольного отношения порядка и произвольного множества, то есть в любом подмножестве рассматриваемого множества есть наименьший элемент относительно рассматриваемого отношения порядка, мы получаем трансфинитную индукцию.
Теорема 1. Пусть есть некоторое вполне упорядоченное множество M и есть некоторая последовательность утверждений 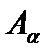 , занумерованных элементами
, занумерованных элементами 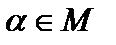 . При этом доказываются два утверждения: 1) утверждение
. При этом доказываются два утверждения: 1) утверждение 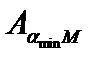 истинно; 2) Из того, что для любого
истинно; 2) Из того, что для любого 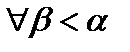 все
все 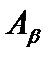 истинны, следует, что и
истинны, следует, что и 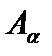 истинно. Тогда утверждение
истинно. Тогда утверждение 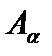 истинно
истинно 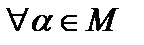 .
.
 Пусть утверждения 1) и 2) выполняются, но среди
Пусть утверждения 1) и 2) выполняются, но среди 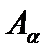 есть неверное утверждение. Рассмотрим множество E всех неверных утверждений. Оно непусто, поскольку хотя бы одно утверждение неверно. Возьмем в нем наименьший элемент
есть неверное утверждение. Рассмотрим множество E всех неверных утверждений. Оно непусто, поскольку хотя бы одно утверждение неверно. Возьмем в нем наименьший элемент 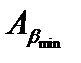 , то есть такой элемент, который меньше любого другого элемента множества E (это можно сделать, поскольку
, то есть такой элемент, который меньше любого другого элемента множества E (это можно сделать, поскольку 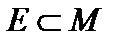 , а множество M вполне упорядочено). Тогда для него утверждение
, а множество M вполне упорядочено). Тогда для него утверждение 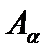 неверно, а для предыдущего элемента ещё верно, что противоречит свойству 2). ■
неверно, а для предыдущего элемента ещё верно, что противоречит свойству 2). ■
ПРОБЛЕМЫ НАИВНОЙ ТЕОРИИ МНОЖЕСТВ
Кризисы в математике
Первый кризис в математике возник в результате обнаружения несоизмеримости отрезков. Оказалось, что диагональ квадрата со стороной, равной единице (или, что то же самое, гипотенуза равнобедренного треугольника с катетом, равным единице), выражается числом 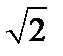 , которое не является рациональным, а представляет собой бесконечную непериодическую дробь. Иначе говоря, данное отношение не может быть выражено дробью
, которое не является рациональным, а представляет собой бесконечную непериодическую дробь. Иначе говоря, данное отношение не может быть выражено дробью 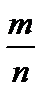 , где
, где 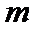 и
и 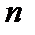 - натуральные числа. Усилиями Теэтета, Евклида, Архимеда и Евдокса, которые разработали метод исчерпывания
- натуральные числа. Усилиями Теэтета, Евклида, Архимеда и Евдокса, которые разработали метод исчерпывания 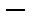 зачаточную форму теории пределов, кризис на том уровне был преодолен. Однако две тысячи лет спустя он возник в видоизмененной форме.
зачаточную форму теории пределов, кризис на том уровне был преодолен. Однако две тысячи лет спустя он возник в видоизмененной форме.
Второй кризис основ математики разразился в конце XVII - начале XVIII в. в ходе попыток обосновать изобретённое Ньютоном и Лейбницем исчисление бесконечно малых. Выход из него нашли О.Коши и К. Вейерштрасс, построив теорию пределов.
С возникновением и развитием теории множеств на рубеже Х1Х-ХХ вв. в математике возник третий кризис, который до сих пор не нашёл своего удовлетворительного разрешения. По сути, это видоизмененная форма всё того же кризиса иррациональности, связанного с тем, что множество иррациональных чисел несчётно и имеет мощность континуума. Множество натуральных чисел N = {1,2,3,...} считается потенциально-бесконечным, потому, что на каждом этапе счёта имеется не более, чем конечное число элементов, а бесконечность понимается как процесс. Несчётные множества уже актуально даны как бесконечные.Но со времён Аристотеля считается, что “Infinitum Actu Non Datur”, то есть не существует актуальной бесконечности потому, что это понятие – внутренне противоречиво и, следовательно, “его использование в математике – недопустимо” (Гаусс). Рассмотрим эти вопросы ближе.
