Формирование алгоритма кинетостатического силового расчета по группам
Формальные правила:
1. Сохраняем абсолютную правую декартовую систему координат, связанную с неподвижной точкой входного звена 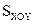 . В этой системе координат рассчитывались кинематические параметры механизма.
. В этой системе координат рассчитывались кинематические параметры механизма.
2. Силы в расчетных схемах раскладываем по положительным осям системы координат. Моменты сил показываем положительными, против вращения часовой стрелки.
3. Статически определимую систему уравнений равновесия сил составляем для группы Ассура или кинематической группы согласно алгоритмической формуле, полученной для исследуемого механизма.
4. Момент силы в уравнениях равновесия запишем относительно точки O системы координат 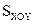 следующим образом:
следующим образом:


 =
=  ,
,
где  - радиус-вектор т.A в системе координат
- радиус-вектор т.A в системе координат 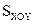 ,
,
 - вектор силы, приложенной в точке
- вектор силы, приложенной в точке 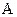 ;
;  - положительные проекции
- положительные проекции  в
в 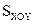 .
.
Пример формирования уравнений равновесия сил в векторной форме приведен в Приложении П 3.3.1., способ 2.
Реакции в КП будем обозначать: - во вращательной: реакция  в кинематической паре
в кинематической паре 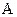 ; реакция
; реакция  в кинематической паре
в кинематической паре  и т.д. - в поступательной: реакция и момент
и т.д. - в поступательной: реакция и момент  в кинематической паре
в кинематической паре 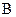 и т.д.
и т.д.
Порядок расчета:
1. Используя найденные при решении задачи кинематического анализа аналоги скоростей и ускорений, рассчитываются ускорения центров масс и угловые ускорения звеньев.
2. Выполняется расчет главного вектора и главного момента сил инерции для звеньев, для которых заданы массы и моменты инерции относительно оси, проходящей через центр масс перпендикулярно плоскости движения (сокращенно – осевые моменты инерции).
3. Для каждого входящего в кинематическую группу (группу Ассура) звена строится расчетная схема, записываются уравнения статики.
4. Для полученной системы линейных уравнений группы формируется матрица коэффициентов при неизвестных 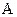 и вектор свободных членов
и вектор свободных членов 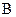 .
.
5. Систему можно решить средствами Mathcad с использованием стандартной процедуры  (уже «знакомой» процедуры
(уже «знакомой» процедуры  , или других, имеющихся в библиотеке стандартных процедур системы Mathcad), дающих решение системы линейных алгебраических уравнений вида
, или других, имеющихся в библиотеке стандартных процедур системы Mathcad), дающих решение системы линейных алгебраических уравнений вида  .
.
Далее, считая, что расчеты п.п. 1, 2 выполнены, построим расчетные схемы для групп Ассура 2-го класса. Для каждой группы сформируем систему линейных уравнений статики: составим уравнения силового равновесия в проекциях на оси координат и уравнение моментов сил относительно т. О системы координат 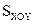 . Если заданы другие внешние силы и моменты (полезного сопротивления или движущие), действующие на звенья механизма, их необходимо поместить на расчетные схемы.
. Если заданы другие внешние силы и моменты (полезного сопротивления или движущие), действующие на звенья механизма, их необходимо поместить на расчетные схемы.
3.1.1.1. Группа Ассура IIВВВ(2,3)
а)
 Дано:
Дано:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Найти: 





Точки приложения реактивных сил - центры вращательных КП
Звено 3
б)


Звено 2
с)


Рис. 14.
Матрица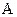





 Вектор
Вектор 

а) 3.1.1.2. Группа Ассура IIВВП(2,3)

Дано:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,
 ,
,  ,
, 
Найти: 





Точка приложения реакции между ползуном 3 и смежным с ним
звеном –точка 
б)

Звено 3

с)
 Звено 2
Звено 2

Рис. 15.
Матрица





 Вектор
Вектор 

а)
 3.1.1.3. Группа Ассура IIВПВ(2,3)
3.1.1.3. Группа Ассура IIВПВ(2,3)
Дано:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Найти: 





Точка приложения реакции между звеньями 2 и 3 – точка 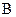
б)
 Звено3
Звено3

с)
 Звено 2
Звено 2

Рис. 16.
Матрица





 Вектор
Вектор 

а) 3.1.1.4. Группа Ассура IIПВП(2,3)
 Дано:
Дано:  ,
,  ,
,  ,
, 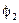 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Найти: 





Точки приложения реакций в поступательных кинематических парах – точки 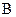 и
и 
б)

Звено3

с)
 Звено 2
Звено 2

Рис. 17.
Матрица ВекторВ
ВекторВ







а)
 3.1.1.5. Группа Ассура IIПВП(2,3)
3.1.1.5. Группа Ассура IIПВП(2,3)
Дано:  ,
, 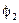 ,
,  ,
,  ,
, 
Найти: 





Звено 2 невесомо. Точка приложения реакции  в поступательной КП между звеньями 2 и 3 – точка
в поступательной КП между звеньями 2 и 3 – точка 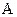 ; реакции
; реакции  в поступательной КП между звеном 3 и смежным с ним звеном –точка
в поступательной КП между звеном 3 и смежным с ним звеном –точка 
б) Звено3 с) Звено 2



 Рис. 18.
Рис. 18.
Матрица 





 Вектор
Вектор 

3.1.1.6. Группа Ассура IIВПП(2,3)
а)
 Дано:
Дано:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Найти: 




Звено 3 движется поступательно вдоль оси 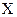 . Точка приложения реакции
. Точка приложения реакции  в поступательной КП между звеньями 2 и 3 – точка
в поступательной КП между звеньями 2 и 3 – точка 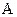 ; реакции
; реакции  в поступательной КП между звеном 3 и смежным с ним звеном – точка
в поступательной КП между звеном 3 и смежным с ним звеном – точка 
б)
 Звено3
Звено3

с)
 Звено2
Звено2

Рис. 19.
Матрица 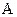





 Вектор
Вектор 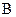

3.1.1.7. Кинематическая группа IВ(0,1)
 Дано:
Дано:  ,
,  ,
,  ,
,  ,
, 
Найти: 



Рис. 20.
Матрица 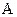 Вектор
Вектор