Аналитическое выравнивание и расчет уравнения регрессии

Тема «Традиционные методы прогнозирования (количественные)»

Вопросы к рассмотрению:

1. Ряды динамики. Тренды. Методы выравнивания ряда. Аналитическое выравнивание. Экстраполяция.

2. Внутригодовая динамика – индексы сезонности, сезонная волна.

3. Причинно-следственные связи. Уравнение регрессии.

Задание 1

Представлены исходные данные по товарообороту магазина города за 2005-2011 гг.:

Показатель	2005г.	2006г.	2007г.	2008г.	2009г.	2010г.	2011г.
Товарооборот города (млн. руб.)

Необходимо провести анализ динамики товарооборота. Результаты расчетов оформить в виде таблицы. Изобразите графически динамику товарооборота магазина за анализируемый период на основе базисных темпов роста.

Рассчитайте динамические средние (двумя способами) и сделайте прогноз величины товарооборота на 2012 год методами экстраполяции и аналитическим выравниванием.

Задание 2экстраполяции и аналитическим выравниванием.

Прожиточный минимум населения России в 2012 г. (в среднем на душу населения, руб.) составил:

01.01.2012г.
01.02.2012г.	7201, 4
01.03.2012г.	7218,9
01.04.2012г.	7234,3
01.05.2012г.	7254,2
01.06.2012г.	7277,2
01.07.2012г.	7293,4
01.08.2012г.	7186,1
01.09.2012г.	7286,2

Для анализа динамики прожиточного минимума населения РФ в 2012 г. вычислите:

1. Среднемесячный прожиточный минимум

2. Темпы роста прожиточного минимума цепные и базисные (к январю месяцу)

3. Среднемесячный темп роста прожиточного минимума.

4. Применить возможные исходя из условия методы прогнозирования.

Сделайте выводы.

Задание 3.

Имеются следующие данные о количестве разводов, оформленных населением г. Волгограда по месяцам 2011-2013 г.г.:

Годы

Январь

Февраль

Март

Апрель

Май

Июнь

Июль

Август

Сентябрь

Октябрь

Ноябрь

Декабрь

Определить общую тенденцию внутригодовой динамики и темпы роста (применение методов выравнивания ряда динамики – укрупнения, скользящей средней).

Определить индексы сезонности методом постоянной средней, изобразить графически. Определить, как можно использовать полученную информацию для прогнозирования и планирования деятельности органов ЗАГС на 2014 год.

Задание 4

Имеются следующие данные по магазинам:

Товарооборот, млн. руб., X	Товарные запасы, Y

Найти:

1.Для подтверждения зависимости между объемом товарооборота и величиной товарных запасов нанесите исходные данные на график корреляционного поля и сделайте выводы.

2.Для установления практической значимости полученной модели вычислите соответствующий показатель тесноты связи.

3. В целях синтезирования модели зависимости суммы товарных запасов от объема товарооборота, вычислите параметры уравнения связи и, определив теоретические (прогнозные) уровни запасов, нанесите их на график корреляционного поля.

Задание самостоятельное – на оценку

По данным Минэкономразвития РФ применить все возможные методы прогнозирования к выбранным наиболее важным (и стабильным) показателям для анализа и прогноза.

Сравнить полученные прогнозные значения с представленными в таблице. Какие методы прогнозирования кроме количественных влияют на прогнозные значения?

				отчет			оценка	прогноз
Цены на нефть Urals (мировые), долл. / барр.							97,6
Добыча нефти, млн. тонн		494,3	505,3	512,4	518,7	520,6
Численность населения, млн.чел.	142,7	142,8	142,8	143,0	143,2	143,5	143,7	143,9
Численность населения трудоспособного возраста	89,5	89,0	88,2	87,5	86,6	85,6	84,7	83,6

Краткие теоретические сведения по вопросам и заданиям:

По вопросу 1

Ряды динамики состоят из двух элементов:

· уровень признака (Y);

· время, к которому отнесена величина признака (t).

Ряды динамики, уровни которых характеризуют состояние общественных явлений на определенный момент времени, называются моментными. Если уровни ряда динамики характеризуют развитие общественных явлений за определенный период времени, то данный ряд динамики является интервальным.

Для количественной оценки динамики социально-экономических явлений применяются следующие статистические показатели:

1. Абсолютный прирост (DY) – важнейший показатель динамики, вычисляемый как разница между уровнями ряда динамики. Различают:

1.1. базисный прирост DY, когда все уровни ряда сравнивают с первоначальным:

.

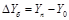1.2. цепной прирост DY, когда за базу сравнения берется уровень предыдущего периода:

.

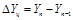Абсолютный прирост может иметь как положительное значение, отображающее нарастание показателя, так и отрицательное значение, показывающее, насколько уровень изучаемого периода ниже базисного (предшествующего).

2. Коэффициент роста (К_р) характеризует отношение двух уровней ряда. Вычисляется базисный и цепной коэффициент роста и если выражается в процентах, то определяется как темп роста (Тр).

На основе базисных темпов роста строится линейный график, отображающий динамику исследуемого явления или процесса, для чего в прямоугольной системе координат по оси абсцисс указывают время, а по оси ординат – темпы роста.

3. Темп прироста (DТр) характеризует абсолютный прирост в относительных величинах и рассчитывается следующим образом:

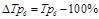
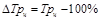
Возможно применение способа расчета темпа прироста на основе средних абсолютных приростов:

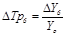
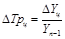
4. Абсолютное значение 1% прироста (А%) определяется также двумя способами, применение которых дает идентичные результаты:

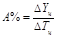
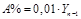
5. Темп наращивания (Тн) является важным статистическим показателем динамики социально-экономических процессов, позволяющим измерять наращивание во времени экономического потенциала:

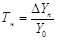
где DY_n – цепной абсолютный прирост,

Y_о – базисный уровень.

Динамические средние представляют собой средние из нескольких смежных значений ряда динамики и являются обобщающими показателями динамики социально-экономических явлений (процессов). В рамках динамического анализа выделяют следующие средние величины:

6. Средний уровень ряда характеризует типическую величину абсолютных уровней. Различают:

6.1. Средний уровень равноинтервального ряда определяется по формуле средней арифметической простой, неравноинтервального – по формуле средней арифметической взвешенной;

6.2.Средний уровень моментного ряда:

· с равными промежутками между датами – по средней хронологической простой;

· с неравными промежутками между датами – по средней хронологической взвешенной.

7. Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики и рассчитывается по следующей формуле:

,

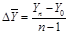где n – число уровней в ряду динамики.

Возможно применение второго способа вычисления среднего абсолютного прироста:

,

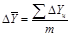где m – число абсолютных приростов.

8. Средний темп роста является обобщающей характеристикой индивидуальных темпов роста ряда динамики и определяется также двумя способами:

- для абсолютных показателей:

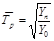
- для относительных показателей:

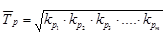
где k_p1, k_p2, k_p3, …, k_pm – цепные коэффициенты роста

m – количество коэффициентов роста

9. Средний темп приростаопределяется на основе взаимосвязи между темпами роста и прироста:

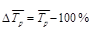
На основе этого показателя производят краткосрочные статистические прогнозирования.

10. Если в статистическом ряду нет резких колебаний цепных показателей динамики, то для определения экстраполируемого (прогнозируемого) уровня применяются следующие расчеты:

10.1. На основе среднего абсолютного прироста применяется формула:

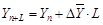
где Y_n+L – прогнозируемый уровень;

Y_n – конечный уровень базисного ряда динамики;

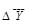– средний абсолютный прирост;

L – срок прогноза.

10.2. На основе среднего темпа роста используется формула:

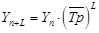
где `Т – средний коэффициент роста.

Для выявления и измерения основной тенденции развития изучаемого явления во времени (тренда) применяются следующие методы преобразования динамических рядов:

1) метод укрупнения интервалов;

2) метод выравнивание ряда по средней скользящей;

3) метод аналитического выравнивания;

4) определение тренда на основе динамических средних (экстраполяция);

5) исчисление показателей сезонных колебаний. В стабильных рядах, в которых нет ярко выраженной тенденции роста, сезонные колебания изучаются на основе постоянного среднего уровня.

Первые два метода группируются в механические методы выявления тренда. Они позволяют сглаживать исходные колебания уровней ряда динамики. Суть этих методов состоит в замене абсолютных данных средними арифметическими, рассчитанными за определенные периоды.

Отличие сглаживания по скользящим средним от метода укрупнения интервалов состоит в расчете средних способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего.

Наиболее эффективным способом выявления основной тенденции развития является аналитическое выравнивание. При этом уровни ряда выражаются в виде функции времени: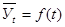

Аналитическое выравнивание может осуществляться по любому рациональному многочлену. Выбор функции производится на основе анализа закономерностей динамики данного явления. Параметры уравнения определяются методом наименьших квадратов.

Для уравнения прямой 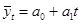система нормальных уравнений имеет вид:

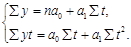
Параметры определяются путем решения системы нормальных уравнений или по формулам:

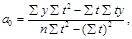
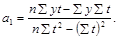
Для определения параметров уравнения прямой строится расчетная таблица (пример расчета см. в таблице 1).

Таблица 1

Аналитическое выравнивание и расчет уравнения регрессии

Годы	Выработка, т. руб. (yi)	t	t2	y×t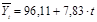
		-4		-240	64,78
		-3		-240	72,61
		-2		-140	80,44
		-1		-100	88,28
					96,11
					103,94
					111,78
					119,61
					127,44
Итого

Если нумерация лет производится как t = 1, …, n, то параметры уравнения вычисляются по формулам, указанным выше. Если же нумерация лет производится как в таблице 7.1.2 ( ), то параметры определяются по формулам:

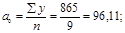
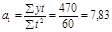
В результате получаем следующее уравнение:

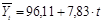
На основе полученного уравнения рассчитываются теоретические значения уровней ряда динамики, определяющие, как менялись значения уровней ряда с течением времени, исходя из выявленной и измеренной тенденции развития изучаемого явления.

По вопросу 2

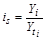Для измерения сезонных колебаний вычисляются индексы сезонности, которые в общем виде определяются по формуле индивидуального индекса сезонности, рассчитываемого для одноименных внутригодовых периодов анализируемого ряда динамики:

где Y_i – исходные (эмпирические) уровни ряда динамики

Yt_i – теоретические (расчетные) уровни ряда динамики, выступающие в качестве базы сравнения.

Так как на сезонные колебания могут накладываться случайные отклонения, для их устранения производится усреднение индивидуальных индексов одноименных внутригодовых периодов анализируемого ряда динамики. Поэтому для каждого периода годового цикла определяются обобщенные показатели в виде средних индексов сезонности, которые свободны от

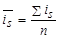влияния тренда и случайных отклонений

где n - число одноименных периодов.

В зависимости от характера тренда рассчитываются средние индексы сезонности способом постоянной средней и способом переменной средней.

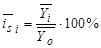На основе постоянного среднего уровня средний индекс сезонности вычисляется в стабильных рядах динамики, где отсутствует ярко выраженный тренд, по следующей формуле:

где `Yi – средний уровень одноименных внутригодовых периодов;

` Y₀ – постоянное общее среднее

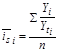В рядах динамики с ярко выраженной основной тенденцией развития сезонные колебания изучаются на основе переменного среднего уровня и средние индексы сезонности рассчитываются по одноименным периодам анализируемого ряда внутригодовой динамики:

По вопросу 3

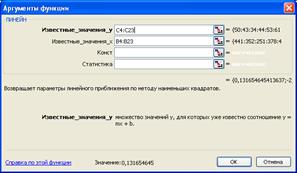
Параметры уравнения связи можно вычислить обычным способом, заполнив указанные столбцы и задав нужные формулы. А можно воспользоваться статистической функцией MS Excel =ЛИНЕЙН(C4:C23;B4:B23), где C4:C23 – массив, содержаний значения товарных запасов Y, B4:B23 – массив, содержаний значения товарооборота Х. Для этого нужно выделить две соседние горизонтальные ячейки, обратиться к нужной функции и заполнить появившееся диалоговое окно, как это указано на рисунке. После этого необходимо щелкнуть в строке формул и нажать сочетание клавиш Ctrl+Shift+Enter. Левая ячейка будет содержать значение коэффициента а₁ при переменной х в уравнении регрессии, правая – значение свободного члена а₀.

Для построения корреляционного поля выделите ячейки со значениями переменной X и переменной Y, вызовите Мастер диаграмм с помощью кнопки , выберите тип диаграммы Точечная. По ее виду делается вывод о наличии линейной связи между объемом товарооборота и величиной товарных запасов.

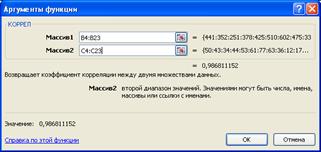
Для подсчета линейного коэффициента корреляции необходимо воспользоваться статистической функцией MS Excel КОРРЕЛ(Массив1; Массив2), где Массив1 – ссылка на ячейки (B4:B23) со значениями переменой X, Массив2 – ссылка на ячейки (C4:C23) со значениями переменой Y.

Для построения линии регрессии на корреляционном поле выделите диаграмму, в меню Диаграмма выберите команду Добавить линию тренда. В появившемся диалоговом окне выберите тип Линейная, в параметрах укажите, что необходимо показывать уравнение на диаграмме.

Для нахождения критических значений t-критерия Стьюдента необходимо воспользоваться статистической функцией MS Excel СТЬЮДРАСПОБР(Вероятность, Степени свободы), где Вероятность – уровень значимости (может быть равен 0,05; 0,01), Степени свободы равны n – 2.