Данная зависимость соответствует неоклассическим критериям.

Построим зависимость V от К

- степенная

V = 0,4352 * К ^1,131077

Данная зависимость не подходит, так как V^//_K > 0

Построим модель зависимости V от К, L и Е

- степенная

V = 7,98 * К ^1,04 * L ^0,24 * Е ^0,15

Данная зависимость не подходит, так как V^//_K >

Из рассмотренных функций, единственной удовлетворяющей неоклассические критерии является

V = 0,3499 * К^0,997 * L ^0,2471

R = 0,7855934

Коэф. множественной корреляции показывает, что функция с точностью 78,55% описывает данное наблюдение

t _p = 3.350571 * 10^-3

t _kp = 2.101

t _pac < t _kp, то есть, с вероятностью 95 % принимается гипотеза, что расчетные и фактичиские значения принадлежат одной генеральной совокупности с точки зрения средней

F _pac = 1.92

F_kp = 2.25

F _pac < F_kp , то есть с вероятностью 95% принимается гипотеза, что значение дисперсии двух выработок равны

Показатели эффективности

Средняя фондоотдача Е_{К =}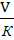

Е_{К = 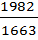= 1,19}

Один станок производит 1,19 ед.

Предельная фондоотдача продукции

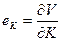; е_{к =} V_к^/ = 0,3499 * 0,997 * 1663 ^-0,063 * 161^0,2471 > 1, 19 ед.

Дополнительно привлеченный станок при неизменных затратах труда произведет 1,19 ед. продукции.

Средняя эффективность использования рабочей силы

E_L=

E_L= 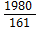=12,3 единиц

На одного работника приходится 12,3 единиц валового выпуска продукции.

Предельная эффективность использования рабочей силы:

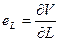
e_L=V_L^/= 0,3499 * 1663^0,997 * 0,2471 *161^-0,7529 = 3,06 ед.

Один дополнительный нанятый работник при неизменной стоимости основных средств будет производить 3,06 единиц продукции.

Предельная норма замещения:

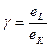
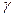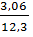= = 0,25

Изъятие одного станка можно компенсировать 0,25 ед. затрат труда таким образом, чтобы валовой выпуск продукции не изменился.

Вклад факторов:

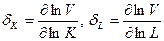
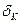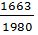= * 1,19 = 0,99

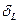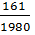= *3,06 = 0,24

Увеличение количества оборудования дает прирост валового выпуска в размер 0,99 ед., а рабочей силы – 0,24

Лабораторная работа № 2 (43121)

І. Проведем графический анализ исходящих данных

ІІ. Построим уравнение регрессии

- многочлен 1-ой степени

y = - 820,6288 + 578,7136 * ( Т-1995)

R = 0,5110591

ϭ² = 3,150027 * 10⁷

F= 3,828755

t = 1,527623 * 10^-8

DW = 1,750489

- многочлен 2-ой степени

y = - 592,8187 + 502,7776 * ( Т-1995) + 3,9967 ( Т-1995)²

R = 0,5113808

ϭ² = 3,148625 * 10⁷

F_р = 3,823923

t = 3,513073 * 10^-7

DW = 1,752933

- степенная

y = 194,5541 * ( Т-1995 +1 )^1,175901

R = 0,4077756

ϭ² = 3,554646 * 10⁷

F_р = 11,04585

t = 4,987609 * 10^-2

DW = 1,547939

- экспонента

y = 548,2819 * е ^{(0,1529523(Т-1995))}

R = 0,4136005

ϭ² = 3,534246 * 10⁷

F_р = 5,551277

t = 4,232573 * 10^-2

DW = 1,585097

Из построенных уравнений регрессии наилучшим является многочлен 2-ой степени

y = - 592,8187 + 502,7776 * ( Т-1995) + 3,9967 ( Т-1995)²

R = 0,5113808

ϭ² = 3,148625 * 10⁷

F_р = 3,823923

t = 3,513073 * 10^-7

DW = 1,752933

Так как, множественный коэф. корреляции самый высокий и R = 0,5113808, остаточная дисперсия наименьшая и ϭ² = 3,148625 * 10⁷

t _PAC = 3.513073 * 10 ^-7

t _KP = 2.101

t _PAC < t _{KP ,} с вероятность 95 % принимается гипотеза, что расчетное и фактическое значение принадлежит одной генеральной совокупности с точки зрения средних.

Так же расчетное значение Дарбин-Уотсона наиболее близко к 2.

ІІІ. Найдем прогнозное значение товарооборота для 2015 и 2016 годов.

С вероятностью 95 % можно утверждать, что значение товарооборота на момент Т_пр будет принадлежать интервалу [ y (T_np) – t _a * ϭ₀; y (T_np) + t _a * ϭ₀], где

t _a = 2,36

ϭ₀ = 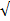ϭ²₀

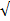ϭ₀ 3,148625 * 10^-7 = 5611,26

Y ( Т₂₀₁₅) = - 592,8187 + 502,7776 (2015-1995) + 3,9967 (2015-1995)²

Y ( Т₂₀₁₅) = -592,8187 + 10 055,55 + 1598,68 = 11 061,41

Т₂₀₁₅ є [ 11 061,41 – 2,36 * 5 611,26; 11 061,41 + 2,36 * 5,611.26]

Т₂₀₁₅ є [ 0; 24 303.98]

Y ( Т₂₀₁₆) = - 592,8187 + 502,7776 * 21 + 3,9967 * 21 ²

Y ( Т₂₀₁₆) = -592,8187 + 10 558,33 + 1 762,54 = 11 727,72

Т₂₀₁₆ є [11 727,72 – 2,36 * 5 611,26; 11 727,72 + 2,36 * 5 611.26]

Т₂₀₁₆ є [ 0; 24 970,2936]

Лабораторная работа № 2 (43121)

І. Проведем графический анализ исходящих данных

ІІ. Построим уравнение регрессии

- многочлен 1-ой степени

y = 150,0428 + 29,94812 * ( Т-1995)

R = 0,4391756

ϭ² = 124794,5

F_р= 5,184703

t = 4,890685 * 10^-8

DW = 1,937515

- многочлен 2-ой степени

y = 341,2466 – 33,78671 * ( Т-1995) + 3,354496 ( Т-1995)²

R = 0,5067135

ϭ² = 114917,1

F_р= 3,894694

t = 1,429428 * 10^-7

DW = 2,046679

- степенная

y = 202,5721 * ( Т-1995 +1 )^0,261466

R = 0,2527191

ϭ² = 114741,2

F_р = 34,84065

t = 4,322139 * 10^-2

DW = 1,690792

- экспонента

y = 245,366 * е ^{(3,809273*10-2(Т-1995))}

R = 0,3325165

ϭ² = 137520,6

F_р = 24,84267

t = 4,212276 * 10^-2

DW = 1,767595

Из построенных уравнений регрессии наилучшим является многочлен 2-ой степени

y = 341,2466 – 33,78671 * ( Т-1995) + 3,354496 ( Т-1995)²

R = 0,5067135

ϭ² = 114917,1

F_р = 3,894694

t = 1,429428 * 10^-7

DW = 2,046679

Так как, множественный коэф. корреляции самый высокий и R = 0,5067135, остаточная дисперсия наименьшая и ϭ² = 114917,1

t _PAC = 1,429428 * 10 ^-7

t _KP = 2.101

t _PAC < t _{KP ,} с вероятность 95 % принимается гипотеза, что расчетное и фактическое значение принадлежит одной генеральной совокупности с точки зрения средних.

Так же расчетное значение Дарбин-Уотсона больше 2.

ІІІ. Найдем прогнозное значение товарооборота для 2015 и 2016 годов.

С вероятностью 95 % можно утверждать, что значение товарооборота на момент Т_пр будет принадлежать интервалу [ y (T_np) – t _a * ϭ₀; y (T_np) + t _a * ϭ₀], где

t _a = 2,36

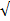ϭ₀ = ϭ²₀

ϭ₀ = 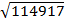= 338,99

Y ( Т₂₀₁₅) = 314,2466 – 33,78671 (2015-1995) + 3,354469 (2015-1995)²

Y ( Т₂₀₁₅) = 1007,3

Т₂₀₁₅ є [ 1 007,3 – 2,36 *338,99 ; 10 073 + 2,36 * 338,99]

Т₂₀₁₅ є [ 207,28; 1 807,31]

Y ( Т₂₀₁₆) = 341,2466 – 33,78671 * (2016-1995) + 3,354469 * (2016-1995) ²

Y ( Т₂₀₁₆) = 1 111,05

Т₂₀₁₅ є [1 111,05 – 2,36 * 338,99; 1 111,05 + 2,36 * 338,99]

Т₂₀₁₅ є [ 311,03; 1 911,06]