Методы случайных квадратов

Пусть n – нечетное составное число, не являющееся степенью целого числа. Методы случайных квадратов – это группа методов, основанная на следующей идее:

Пусть n – нечетное составное число, не являющееся степенью целого числа. Целые x, y – такие случайные числа, что x²≡y²(mod n), x 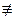±y(mod n). Тогда n\(x²—y²), но n не делит ни (x+y), ни (x—y), а значит НОД(x—y,n) – нетривиальный делитель n.

Методы случайных квадратов ищут случайным образом числа x, y: x²≡y²(mod n), а затем проверяют, что x 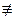±y(mod n).

Замечание: Если x, y – случайные числа, такие что x²≡y²(mod n), то P(x 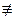±y(mod n)) ≤ 1/2. Действительно, сравнение a≡x²(mod n) имеет 2^k различных корней, если n имеет k различных простых делителей, 2^k—2 из которых подходят к вероятности.

Общий подход к поиску чисел x, y таков: выбирается факторная база S={p₁, p₂, … , p_t}. Как правило, это t первых простых чисел.

Случайно выбирается несколько чисел a_i, вычисляются числа b_i=a_i² mod n и разлагается по факторной базе b_i= . Те числа b_i, которые разложить по базе S не удалось, из дальнейшего рассмотрения исключаются. Всего требуется t+1 пара (a_i, b_i).

Затем из чисел b_i составляется такое произведение B= , c_i 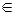{0,1}, что B оказывается полным квадратом (то есть mod 2=0 для всех j). Вектор c находится путем решения соответствующей системы сравнений. Тогда

x= , y= .

Очевидно, данная пара удовлетворяет сравнению x²≡y²(mod n). Если она удовлетворяет еще и условию x 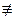±y(mod n), то НОД(x—y,n) есть нетривиальный делитель n. Иначе следует повторить данный метод, выбрав другие пары (a_i, b_i).

Алгоритмы дискретного логарифмирования.

Проблема дискретного логарифмирования в группе Z_p^* состоит в следующем: пусть p – простое число, g – порождающий элемент группы Z_p^* (или, иначе, примитивный корень по модулю p), a=g^x (mod p). Пусть известны g, p, a, но неизвестно x. Требуется найти x, или, иначе, log_ga mod (p—1), то есть вычислить дискретный логарифм.

В отличие от логарифма непрерывного, дискретный логарифм не является дифференцируемой монотонной функцией, его нельзя найти приближенно, разложив в ряд Тейлора, и вообще никакого приближенного значения здесь не может быть, ведь x – целое число.

Дискретное логарифмирование считается сложной проблемой. С этой проблемой связаны и другие теоретико-числовые проблемы, такие как проблема Диффи-Хеллмана, логарифмирование в Z_n. Если удастся решить проблему дискретного логарифма, то приведенные задачи решаются за полиномиальное время.

Метод прямого поиска.

Этот наивный метод является самым трудоемким, он требует O(n) умножений, то есть обладает экспоненциальной сложностью. Состоит он в следующем: вычисляются g⁰, g¹, g²,…, g^p—1 пока не попадется gⁱ≡a(mod p). Полученное i будет искомым дискретным логарифмом i=log_ga (mod p—1).

Пример

p=23, g=5, a=19.

i

gi mod p

19

Ответ: log₅19 mod 22 = 15.