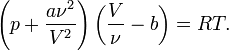Основы термодинамики: внутренняя энергия, число степеней свободы. Закон равномерного распределения энергии по степеням свободы

Внутренняя энергия – энергия хаотичного движения молекул и энергия взаимодействия этих частиц.

Число степеней свободы - наименьшее число независимых координат, определяющих положение и конфигурацию молекулы в пространстве.

Закон равномерного распределения энергии по степеням свободы молекул можно сформулировать следующим образом: статистически в среднем на каждую степень свободы молекул приходится одинаковая энергия. Поступательное движение молекул характеризуется средней кинетической энергией, равной 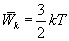. Так как поступательному движению соответствует 3 степени свободы, то в среднем на одну степень свободы движения молекул приходится энергия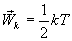

В однородном газе, молекулы которого имеют любое число степеней свободы i, каждая молекула в среднем обладает энергией движения, равной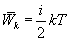

Первое начало термодинамики. Работа газа при изменении его объёма. Теплоёмкость газа.

Превращение энергии. Идёт на изменение энергии U и совершение работы A:

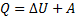
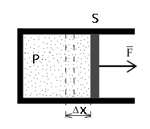Работа газа при изменении его объёма:

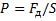
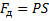
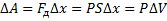
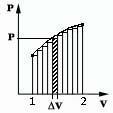
Площадь под графиком с осями P, V пропорциональна работе газа.

Теплоёмкость – количество теплоты, переданной системе.

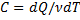(удельная теплоёмкость тела)

Теплоёмкость при постоянном объёме:

V=const (A=0)

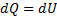
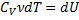
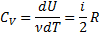
Теплоёмкость при постоянном давлении:

P=const

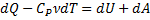
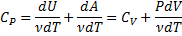
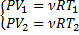⇒ PdV=νRdT ⇒

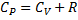(уравнение Майера)

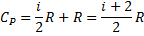
Первое начало термодинамики. Применения первого начала термодинамики к изопроцессам.

Изохорный процесс:

V=const, dV=0, dA=PdV=0

⇒ Первое начало: dQ=dU=C_VνdT

Изобарный процесс:

P=const

Первое начало: dQ=dU+dA

R=A/νdT (универсальная газовая постоянная)

Изотермический процесс:

T=const

Первое начало: dQ=dA

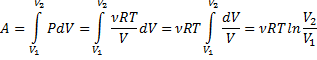
Адиабадный процесс:

Процесс при котором отсутствует теплообмен, т.е. dQ=0.

Первое начало: dU+dA=0

dA=-dU

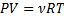
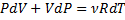
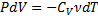
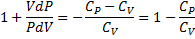
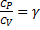(показатель адиабаты, или коэффициент Пуассона)

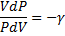
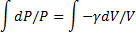
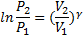
PV^γ=const

Реальные газы. Уравнение Ван-дер-Вальса.

Термическим уравнением состояния (или, часто, просто уравнением состояния) называется связь между давлением, объёмом и температурой.

Для одного моля газа Ван-дер-Ваальса оно имеет вид:

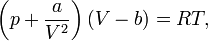
где

• p — давление,
• V — объём,
• T — абсолютная температура,
• R — универсальная газовая постоянная.

Видно, что это уравнение фактически является уравнением состояния идеального газа с двумя поправками. Поправка a учитывает силы притяжения между молекулами (давление на стенку уменьшается, т.к. есть силы, втягивающие молекулы приграничного слоя внутрь), поправка b — силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами).

Для ν молей газа Ван-дер-Ваальса уравнение состояния выглядит так: