Классы эквивалентности
Подмножество элементов эквивалентных данному называется его классом эквивалентности. Пишут:
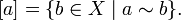
Пусть 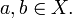 Тогда либо
Тогда либо 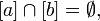 либо
либо 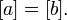 Таким образом отношение эквивалентности порождает разбиение множества на непересекающиеся классы эквивалентности. Семейство таких классов образует множество, называемое фактор-множеством и обозначаемое
Таким образом отношение эквивалентности порождает разбиение множества на непересекающиеся классы эквивалентности. Семейство таких классов образует множество, называемое фактор-множеством и обозначаемое 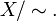
Примеры
Равенство  элементов произвольного множества.
элементов произвольного множества.
Сравнение по модулю 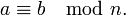
Отношение конгруэнтности 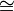 в Евклидовой геометрии.
в Евклидовой геометрии.
Отношение подобия 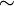 в Евклидовой геометрии.
в Евклидовой геометрии.
Отношение параллельности прямых  в Евклидовой геометрии.
в Евклидовой геометрии.
Отношение эквивалентности двух фундаментальных последовательностей рациональных чисел: 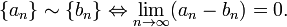 Классами эквивалентности являются действительные числа.
Классами эквивалентности являются действительные числа.
Равенство измеримых функций почти всюду.
Равенство случайных величин почти наверное.
Отношение порядка
Бинарное отношение 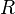 на множестве
на множестве 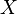 называется отношением порядка, или отношением частичного порядка, если имеют место
называется отношением порядка, или отношением частичного порядка, если имеют место
Рефлексивность: 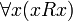
Транзитивность: 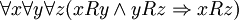 ;
;
Антисимметричность: 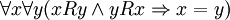 .
.
Множество 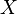 , на котором введено отношение частичного порядка, называется частично упорядоченным.
, на котором введено отношение частичного порядка, называется частично упорядоченным.
Отношение 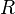 , удовлетворяющее условиям рефлексивности, транзитивности, антисимметричности также называют нестрогим, или рефлексивным частичным порядкоми обычно обозначают символом
, удовлетворяющее условиям рефлексивности, транзитивности, антисимметричности также называют нестрогим, или рефлексивным частичным порядкоми обычно обозначают символом 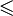 . Если условие рефлексивности заменить на условие антирефлексивности:
. Если условие рефлексивности заменить на условие антирефлексивности:
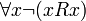 ,
,
то получим определение строгого, или антирефлексивного частичного порядка, обозначаемое обычно символом 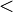 . В общем случае, если
. В общем случае, если 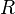 — транзитивное, антисимметричное отношение, то
— транзитивное, антисимметричное отношение, то
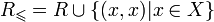 — рефлексивный порядок
— рефлексивный порядок
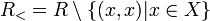 — антирефлексивный порядок.
— антирефлексивный порядок.
Отношение частичного порядка 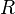 называется линейным порядком, если выполнено условие
называется линейным порядком, если выполнено условие
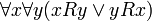
Множество 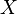 , на котором введено отношение линейного порядка, называется линейно упорядоченным, или цепью.
, на котором введено отношение линейного порядка, называется линейно упорядоченным, или цепью.
Отношение 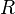 , удовлетворяющее только условиям рефлексивности и транзитивности, называется квазипорядком, или предпорядком.
, удовлетворяющее только условиям рефлексивности и транзитивности, называется квазипорядком, или предпорядком.
1.4
Абелева или коммутативная группа есть группа, в которой групповая операция является коммутативной. Название дано в честь норвежского математика Нильса Хенрика Абеля (1802-1829), за его вклад в исследование групп преобразований.
Конечнопорождённые абелевы группы изоморфны произведениям циклических групп. Конечные абелевы группы изоморфны произведениям конечных циклических групп.
Примеры
Любое кольцо является коммутативной (абелевой) группой по своему сложению. В том числе ивещественные числа с операцией сложения.
Обратимые элементы коммутативного кольца образуют абелеву группу по умножению. Например, вещественные числа, не равные нулю, с операцией умножения.
Группа параллельных переносов в линейном пространстве.
Любая циклическая группа G является коммутативной(абелевой), потому что для любых x и y из Gверно, что xy = aman = am + n = an + m = anam = yx. В частности, целые числа Z образуют коммутативную группу по сложению, также как и вычеты по модулю Z/nZ.
Свойства  Править
Править
Пусть n — натуральное число, а x — элемент коммутативной группы G с операцией, обозначаемой сложением, тогда nx можно определить как x + x + … + x (n раз) и (−n)x = −(nx). Таким образом, G становитсямодулем над кольцом Z целых чисел. В действительности модули над Z однозначно задаются абелевыми группами.
Утверждения и теоремы, верные для абелевых групп (то есть модулей над кольцом главных идеалов Z), зачастую могут быть обобщены на модули над произвольным кольцом главных идеалов. Типичным примером является классификация конечнопорожденных абелевых групп.
Пусть f, g : G → H — два гомоморфизма групп между абелевыми группами, тогда их сумма f + g, заданная как (f + g)(x) = f(x) + g(x), тоже является гомоморфизмом (это неверно, если H некоммутативная группа). Тем самым множество Hom(G, H) всех групповых гомоморфизмов из G в H само становится абелевой группой.
По аналогии с размерностью у векторных пространств, каждая абелева группа имеет ранг. Он определён какмощность максимального линейно-независимого подмножества группы. Целые и рациональные числа имеют ранг один, как и любая их подгруппа. В то время как абелевы группы ранга один без элементов бесконечного порядка хорошо изучены, даже группы конечного порядка изучены плохо. Абелевы группы бесконечного порядка могут быть устроены очень сложно и вызывают много нерешённых вопросов, зачастую привязанных к вопросам теории множеств.
Циклическая группа
В теории групп группа 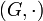 называется циклической, если она порождена одним элементом a, то есть все её элементы являются степенями a (или, если использовать аддитивную терминологию, представимы в видеna, где n — целое число.)
называется циклической, если она порождена одним элементом a, то есть все её элементы являются степенями a (или, если использовать аддитивную терминологию, представимы в видеna, где n — целое число.)
Таким образом, мы называем G циклической, если G = {an| 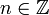 }. Иначе говоря, группа G циклическая, если в G любая подгруппа, содержащая a, совпадает с G. Это следует из того, что в такой подгруппе должны содержаться все степени элемента a.
}. Иначе говоря, группа G циклическая, если в G любая подгруппа, содержащая a, совпадает с G. Это следует из того, что в такой подгруппе должны содержаться все степени элемента a.
Например, если G = {e, g1, g2, g3, g4, g5}, то G циклическая. В этом случае можно заметить, что G устроена также, как и группа {0, 1, 2, 3, 4, 5} с операцией сложения по модулю 6 (говоря формально, G изоморфна ей). Изоморфизм строится, если в соответствие g поставить 1 из второй группы.
Для каждого числа существует единственная (с точностью до изоморфизма) циклическая группа такогопорядка. Также существует ровно одна бесконечная циклическая группа. Из-за такой простоты их строения циклические группы досконально изучены и классифицированы.
Несмотря на своё название, группа не обязательно должна буквально представлять собой «цикл». Может случиться так, что все степени 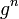 будут различными. Порождённая таким образом группа называетсябесконечной циклической группой и изоморфна группе целых чисел по сложению (
будут различными. Порождённая таким образом группа называетсябесконечной циклической группой и изоморфна группе целых чисел по сложению ( 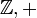 ).
).
Поскольку все циклические группы абелевы, их часто обозначают как 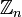 , хотя некоторые математики такого обозначения избегают, обозначая их как факторгруппы целых чисел (
, хотя некоторые математики такого обозначения избегают, обозначая их как факторгруппы целых чисел ( 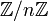 ), чтобы не спутать с другими общепринятыми обозначениями.
), чтобы не спутать с другими общепринятыми обозначениями.
Свойства
Каждая циклическая группа изоморфна группе {0, 1, 2, … n - 1} со сложением по модулю n или 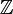 , группе целых чисел по сложению. Таким образом, для понимания устройства всех циклических групп достаточно изучить только эти. Такое свойство делает циклические группы очень лёгкими для изучения. Известно много интересных свойств таких групп. Пусть дана циклическая группа G порядка n (возможно, бесконечного). Тогда для всех g из G верно слеующее:
, группе целых чисел по сложению. Таким образом, для понимания устройства всех циклических групп достаточно изучить только эти. Такое свойство делает циклические группы очень лёгкими для изучения. Известно много интересных свойств таких групп. Пусть дана циклическая группа G порядка n (возможно, бесконечного). Тогда для всех g из G верно слеующее:
G абелева; то есть групповая операция коммутативна: ab = ba. Это верно, поскольку (a + b) mod n = (b+ a) mod n.
Если n < 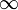 , то
, то 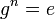 , поскольку n mod n = 0.
, поскольку n mod n = 0.
Если же n = 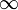 , то существуют только два порождающих элемента: 1 и -1 (в обозначениях
, то существуют только два порождающих элемента: 1 и -1 (в обозначениях 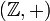 ).
).
Каждая подгруппа G циклична.
Gn изоморфна 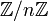 (факторгруппа
(факторгруппа 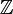 по
по 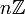 ), поскольку
), поскольку 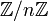 = {0 +
= {0 + 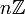 , 1 +
, 1 + 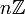 , 2 +
, 2 + 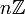 , …, n - 1 +
, …, n - 1 + 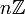 }
} 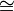 {0, 1, 2, 3, 4, … n - 1} с сложением по модулю n.
{0, 1, 2, 3, 4, … n - 1} с сложением по модулю n.
Порождающими 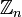 являются все числа от 1 до n, которые взаимно просты с n; их количество равно φ(n), где φ — функция Эйлера. Более общо, если d является делителем n, то число элементов порядка d в
являются все числа от 1 до n, которые взаимно просты с n; их количество равно φ(n), где φ — функция Эйлера. Более общо, если d является делителем n, то число элементов порядка d в 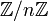 равно φ(d). Порядок класса вычета m равен n / НОД(n,m).
равно φ(d). Порядок класса вычета m равен n / НОД(n,m).
Если p — простое число, то группа порядка p циклическая и единственна с точностью до изоморфизма (это следует из теоремы Лагранжа).
Прямое произведение двух циклических групп 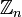 и
и 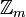 циклично тогда и только тогда, когда n и m взаимно просты. Например,
циклично тогда и только тогда, когда n и m взаимно просты. Например, 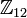 является прямым произведением
является прямым произведением 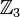 и
и 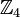 , но не
, но не 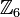 и
и 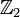 .
.
Основная теорема о конечнопорождённых абелевых группах утверждает, что любая конечнопорождённая абелева группа единственным образом разлагается в прямое произведение примарных циклических групп. Примарной группой может быть циклическая группа 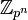 , где p — простое число, или
, где p — простое число, или 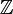 .
.
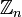 также являются коммутативными кольцами (по сложению и умножению). Если p — простое число, то
также являются коммутативными кольцами (по сложению и умножению). Если p — простое число, то 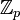 — конечное поле, также обозначаемое Fp или GF(p). Каждое конечное поле с p элементами изоморфно Fp.
— конечное поле, также обозначаемое Fp или GF(p). Каждое конечное поле с p элементами изоморфно Fp.
Мультипликативная группа любого конечного поля является циклической (она порождается элементом поля наибольшего порядка).
1.5
Изоморфизм, одно из основных понятий современной математики, возникшее сначала в пределах алгебры в применении к таким алгебраическим образованиям, как группы, кольца, поля и т. п., но оказавшееся весьма существенным для общего понимания строения и области возможных применений каждого раздела математики.
Понятие И. относится к системам объектов с заданными в них операциями или отношениями. В качестве простого примера двух изоморфных систем можно рассмотреть систему R всех действительных чисел с заданной на ней операцией сложения x=x1+x1 и систему Рположительных действительных чисел с заданной на ней операцией умножения y=y1y2. Можно показать, что внутреннее "устройство" этих двух систем чисел совершенно одинаково. Для этого достаточно систему R отобразить в систему Р, поставив в соответствие числу х из Rчисло у=ax(а> 1) из Р. Тогда сумме x=x1+x2 будет соответствовать произведение y = y1y2 чисел 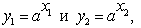 соответствующих x1иx2. Обратное отображение Р на R имеет при этом вид x= logay. Из любого предложения, относящегося к сложению чисел системы R, можно извлечь соответствующее ему предложение, относящееся к умножению чисел системы Р. Например, если вRсумма
соответствующих x1иx2. Обратное отображение Р на R имеет при этом вид x= logay. Из любого предложения, относящегося к сложению чисел системы R, можно извлечь соответствующее ему предложение, относящееся к умножению чисел системы Р. Например, если вRсумма
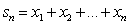
членов арифметической прогрессии выражается формулой
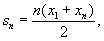
то в Р произведение
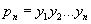
членов геометрической прогрессии выражается формулой
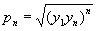
(умножению на n в системе R соответствует при переходе к системе Р возведение в n-ю степень, а делению на два — извлечение квадратного корня).
Изучение свойств одной из изоморфных систем в значительной мере (а с абстрактно-математической точки зрения — полностью) сводится к изучению свойств другой. Любую систему объектов S', изоморфную системе S, можно рассматривать как "модель" системы S ("моделировать систему S при помощи системы S' ") и сводить изучение самых разнообразных свойств системы S к изучению свойств "модели" S'.
Общее определение И. систем объектов с заданными на них в конечном числе отношениями между постоянным для каждого отношения числом объектов таково. Пусть даны две системы объектов Sи S', причём в первой определены отношения
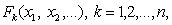
а во второй — отношения
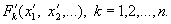
Системы S и S' с указанными в них отношениями называются изоморфными, если их можно поставить в такое взаимно однозначное соответствие
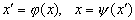
(где х —произвольный элемент S, а x' —произвольный элемент S'), что из наличия Fk (x1,x2,...) вытекает F'k(х'1,х'2,...), и наоборот. Само указанное соответствие называется при этом изоморфным отображением, или изоморфизмом. [В приведённом выше примере в системе Rопределено отношение F(x, x1, x2), где x = x1 +x2, в системе Р — отношение F'(y, y1, y2), где у=у1у2; взаимно однозначное соответствие устанавливается по формулам у=ax, х=1ogay.]
Понятие И. возникло в теории групп, где впервые был понят тот факт, что изучение внутренней структуры двух изоморфных систем объектов представляет собой одну и ту же задачу.
Аксиомы любой математической теории определяют систему объектов, изучаемую этой теорией, всегда только с точностью до И.: аксиоматически построенная математическая теория, применимая к какой-либо одной системе объектов, всегда полностью применима и к другой. Поэтому каждая аксиоматически изложенная математическая теория допускает не одну, а много "интерпретаций", или "моделей" (см., например, в ст. Геометрия, раздел Истолкование геометрии).
Понятие И. включает в себя как частный случай понятие гомеоморфизма, играющее основную роль в топологии.
Частным случаем И. является автоморфизм — взаимно однозначное отображение
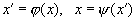
системы объектов с заданными отношениями Fk(x1, x2, ...) на самоё себя, при котором из Fk(x1, x2, ...) вытекает F'k(x'1, x'2, ...), и наоборот. Это понятие тоже возникло в теории групп, но потом оказалось существенным в самых различных разделах математики.
1.6
Делитель нуля
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 16 августа 2012; проверки требует 1 правка.
В абстрактной алгебре ненулевой элемент a кольца называется левым делителем нуля, если существует ненулевое b такое, что ab = 0.
Аналогично, ненулевой элемент a кольца является правым делителем нуля, если существует ненулевое b такое, что ba = 0.
Элемент, который одновременно является и правым, и левым делителем нуля, называется делителем нуля. Если умножение в кольце коммутативно, то понятия правого и левого делителя совпадают. Ненулевой элемент кольца, который не являются ни правым, ни левым делителем нуля, называется обычным элементом.
Пример: в кольце 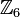 элементы 2, 3, 4 — делители нуля.
элементы 2, 3, 4 — делители нуля.
Ассоциативное коммутативное кольцо 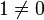 без делителей нуля называется областью целостности.
без делителей нуля называется областью целостности.
ОПРЕДЕЛЕНИЕ КОЛЬЦА
Определение 1. Множество R с операциями сложения + и умножения называется кольцом, если относительно сложения это множество является абелевой группой, а сложение с умножением связывает закон дистрибутивности
8x; y; z 2 R x (y + z) = xy + xz; (x + y)z = xz + yz:
Если операция умножения обладает свойством ассоциативности, то кольцо называется ассоциативным. В основном, мы будем рассматривать ассоциативные кольца.
Если в кольце R содержится нейтральный по умножению элемент (единица 1), то кольцо называется кольцом с единицей.
Если операция умножения в кольце R коммутативна, то кольцо называется коммутативным.
Определение 2. Ассоциативное кольцо с единицей, в котором каждый ненулевой элемент имеет обратный (т.е. множество R n f0g с операцией умножения является группой) называется телом.
Определение 3. Коммутативное тело называется полем.
1.7
Кольца, тела и поля
Алгебраическую структуру с двумя бинарными операциями 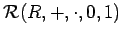 называется кольцом, если выполняются следующие соотношения:
называется кольцом, если выполняются следующие соотношения:
-
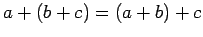 ;
; -
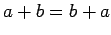 ;
; -
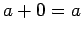 ;
; -
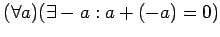 ;
; -
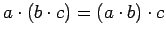 ;
; -
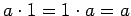 ;
; -
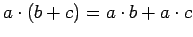 и
и 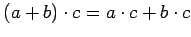 .
.
Другими словами, алгебра 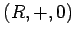 является абелевой группой, алгебра
является абелевой группой, алгебра 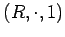 -- моноидом, а операция умножения дистрибутивна относительно сложния.
-- моноидом, а операция умножения дистрибутивна относительно сложния.
Можно доказать, что в кольце имеет место аннулирующее свойство нуля: 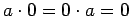 .
.
В качестве примеров колец можно привести:
- кольцо действительных чисел с привычными операциями сложения и умножения --
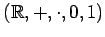 . Действительно, по сложению имеем абелеву группу, тогда как по умножению -- лишь моноид (обратный к нулю элемент не определён).
. Действительно, по сложению имеем абелеву группу, тогда как по умножению -- лишь моноид (обратный к нулю элемент не определён). - кольцо квадратных матриц степени
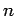 --
-- 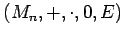 , где 0 и
, где 0 и 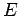 -- соответственно нулевая и единичная матрица. Также только моноид по умножению, потому что обратная матрица существует не для каждой квадратной матрицы.
-- соответственно нулевая и единичная матрица. Также только моноид по умножению, потому что обратная матрица существует не для каждой квадратной матрицы.
В некоторых кольцах существуют делители нуля, т.е. такие элементы 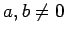 , что
, что 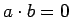 . Для обычной арифметики это кажется удивительным и не выполняется, тогда как для приведённого выше примера кольца матриц можно найти делители нуля:
. Для обычной арифметики это кажется удивительным и не выполняется, тогда как для приведённого выше примера кольца матриц можно найти делители нуля:
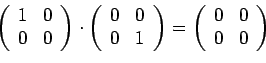
Кольцо без делителей нуля называется областью целостности. Пример такой алгебры -- кольцо целых чисел с операциями сложения и умножения. Кольцо без делителей нуля, множество ненулевых элементов которого является группой по умножению, называется телом. Тело с коммутативной операцией умножения называется полем.
Кольца рациональных, действительных и комплексных чисел с операциями арифметического сложения и умножения являются полями.
Задания для самоподготовки. Задана алгебра 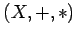 с двумя бинарными операциями. Проверить свойства этой операции и указать, к какому типу эта алгебра относится. с двумя бинарными операциями. Проверить свойства этой операции и указать, к какому типу эта алгебра относится.
|
1.8
Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:
1) два комплексных числа z1 = (x1, y1) и z2 = (x2, y2) называются равными, если x1 = x2 и y1 = y2;
2) суммой комплексных чисел z1 и z2 называется комплексное число z вида
z = (x1 + x2, y1 + y2);
3) произведением комплексных чисел z1 и z2 называется комплексное число
z = (x1x2 - y1y2, x1y2 + x2y1);
4) множество комплексных чисел 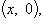
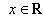 , отождествляется с множеством действительных чисел R.
, отождествляется с множеством действительных чисел R.
Разностью комплексных чисел z1 и z2 называется комплексное число z такое, что z2 + z = z1, откуда находим z = z1 - z2 = (x1 - x2, y1 -y2).
Частным комплексных чисел z1 и z2 называется комплексное число z такое, что 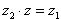 . Отсюда находим
. Отсюда находим
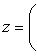
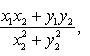
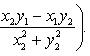
Комплексное число (0, 1) обозначается символом i = (0, 1). Тогда 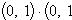
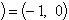 , т. е. i2 = -1. Произвольное комплексное число z можно записать в виде
, т. е. i2 = -1. Произвольное комплексное число z можно записать в виде
z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.
Эта запись называется алгебраической формой комплексного числа. Комплексное число 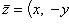
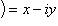 называетсясопряженным по отношению к комплексному числу z = (x, y) = x + iy.
называетсясопряженным по отношению к комплексному числу z = (x, y) = x + iy.

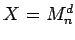 -- множество диагональных матриц степени
-- множество диагональных матриц степени 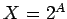 ,
, 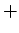 --
-- 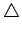 , симметрическая разность множеств, а
, симметрическая разность множеств, а 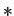 --
-- 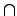 , пересечение множеств;
, пересечение множеств;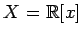 -- множество многочленов от переменной
-- множество многочленов от переменной 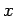 с действительными коэффициентами.
с действительными коэффициентами.