Дөңес жиындағы тегіс бейнелеудің қасиеті

Еселі интегралдарда айнымалыны алмастыруда тегіс бейнелеудің кейбір қасиеттері қажет болады. Функция 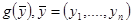компактылы өлшемді 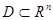облысында анықталған және 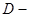да интегралданатын болсын. мына интегралды білдіретін болсын

.

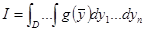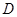және 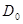жиындарының ішкі нүктелерінің арасындағы өзара бірмәнді сәйкестікті тағайындайтын, 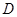жиынындағы 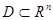өлшемді компактының 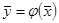бейнелеуін қарастырамыз. 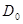-де анықталған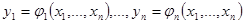 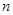функцияның жүйесімен берілген 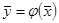бейнелеуді ескереміз. Бұл функцияның әрқайсысы 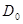-де барлық үзіліссіз дербес туындылы болады деп есептейік.

Ескерту. 1) Функция 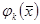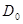-де анықталған қисықсызықты координата деп аталады.

2) Бейнелеу 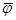-дің өзара бірмәнділік шарты: 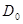облысының ішкі нүктелері үшін 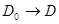, 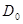облысының әрбір нүктесінде осы бейнелеудің якобиандары нөлден өзгеше болғанда ғана қанағаттандырылады(кері бейнелеу туралы теорема). Облыстағы тегіс бейнелеу туралы тұжырымды құрамыз және дәлелдейміз.

Теорема 12. 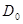дөңес және тұйық жиын және 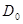жиынында 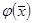тегіс функция болсын. Сондай-ақ 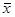және 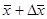нүктелері 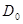-ге тиісті болсын. Онда мынадай 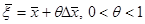нүктесі табылады да, 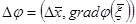болады.

Дәлелдеуі. Бір 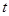айнымалылы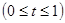 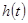функциясын қарастырамыз:

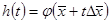
Мұнда 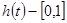кесіндісіндегі тегіс функция.

Олай болса, оған шектеулі өсімшенің Лагранж формуласын қолдануға болады. Онда мынадай 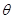, 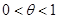саны табылады да, 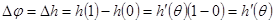болады. Функция 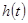күрделі функция 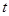-дан және күрделі функцияны дифференциалдау ережесі бойынша мынаны аламыз:

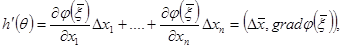мұнда 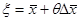. Дәлелденді.

Теорема 13. 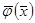- D облысындағы D₀ дөңес компактың тегіс бейнелеуге болады. Онда мынадай 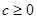саны табылады да, кез-келген 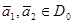нүктелері үшін

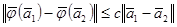теңсіздігі дұрыс болады. Мұндағы 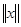-евклидтік метрикадағы (өлшемдегі) вектор ұзындығы.

Дәлелденуі. Теорема 12-ден 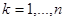кезінде мынаны аламыз.

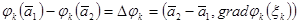
Мұндағы 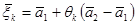және 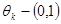интервалының кейбір саны. Коши теңсіздігін 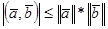қолданып, мынаны аламыз:

.

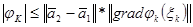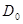компакт және 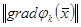функциясы 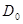-де үзіліссіз болғандықтан, ол бұл компактіде кейбір 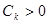тұрақтысымен шектеледі. Осыны және сандық теңсіздікті 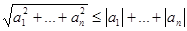қолданып, 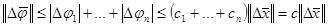аламыз, мұндағы 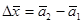. Дәлелденді.

Бейнелеу 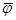-дің Якоби матрицасы 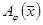арқылы белгілейік: 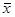нүктесінде .

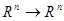Анықтама 17. Вектор 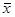-тің 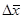өсімшесінің 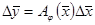сызықтық бейнелеуі деп 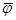бейнелеудің дифференциалын айтады және 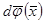символымен белгіленеді. 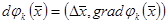- вектор.
Теорема 14. 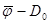дөңес компактінің тегіс бейнелеуі және 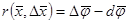болсын. Онда келесі бірқалыпты шектің орны бар 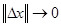кезінде

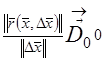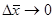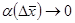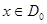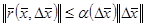. Басқаша айтқанда, мынадай кезінде сандық функция табылады да, барлық үшін теңсіздігі дұрыс болады.

Дәләлдеуі: 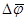және 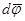векторларының 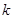-шы координатасын қарастырамыз. Анықтама бойынша 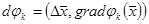, ал Теорема 12 бойынша кейбір 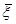кезінде мынаны аламыз: 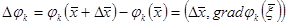. Олай болса, 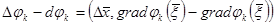. Енді 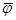бейнелеуінің дербес туындысы 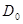компактіде үзіліссіз болғандықтан, онда 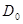-де оның бірқалыпты үзіліссіздігі ретінде мынаны аламыз:

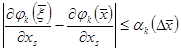, мұндағы 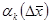тек қана 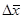- ке тәуелді және 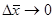кезінде 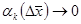. Бұдан Коши теңсіздігің қолданып мынаны аламыз: 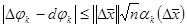, олай болса, 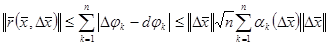, әрі 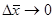кезінде .

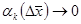Дәлелденді.

Еселі интегралдарға айнымалыны ауыстыру формуласы

Жордан бойынша өлшемді Риманның қос интегралы

Анықтама 15: Жордан бойынша өлшенетін, шектелген D облысының 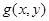функциясын Риманның жалпыланған қос интегралы деп I санын айтады, егер кез-келген 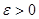үшін мынадай 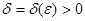саны табылып, әрбір 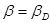бөлінуі үшін 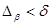шартымен 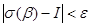теңсіздігі орындалса.

Жалпыланған қос интегралды база бойынша шек ретінде қарастыруға болады, Бұл базаны 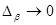символымен белгілейміз. Ол 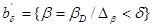шартымен анықталған 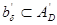жалғауынан құрылады. Шындығында да, 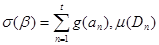функциясы 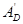жиынында анықталған, ал оның база бойынша шегі 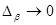және ол D обылысы бойынша жалпыланған қос интеграл болады.

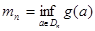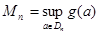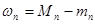, , болсын. Онда Дарбудың жоғарғы және төменгі қосындысын келесі өрнекке сәйкес анықтаймыз:

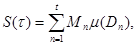
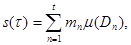және омега қосындысын 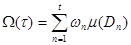өрнегімен анықтаймыз.

Кейбір P тіктөртбұрышы үшін 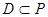болсын.

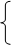
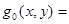
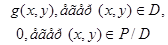деп ұйғарып , барлық Р тіктөртбұрышын да 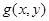функциясын анықтаймыз.

Анықтама 16 : Егер 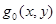функциясы Р тіктөртбұрышында Риман бойынша интегралданатын болса, онда 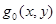функциясының Р бойынша J қос интегралы 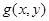функциясының D жиыны бойынша Риман қос интегралы деп аталады, яғни анықтама бойынша 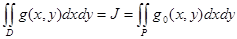болады.

Теорема 6: Жалпыланған қос I интегралының бар болуы үшін, J интегралының бар болуы қажетті және жеткілікті, сонымен бәрге онда I=J.

Дәлелдеуі:

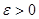1. Тіктөртбұрыш P және J интегралы бар болсын. Онда интегралыдану критерийіне байланысты , кез-келген үшін, мынадай Т бөліну табылады да, 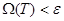. Т бөліну 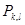тіктөртбұрыштарынан тұрады. 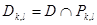деп аламыз. Онда D жиынының 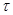бөлінуін аламыз. 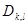жиындағы 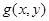функциясының тербелісі 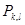-дағы оның тербеліснен аспайды, сондықтан 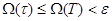аламыз, яғни интегралдану киртерийіне байланысты жалпыланған I интегралы табылады. Осыған ұқсас, 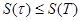теңсіздігін алуға болады, сондықтан 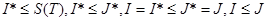. Дарбудың төменгі қосындысы үшін ұқсас теңсіздіктерден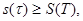 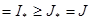аламыз. Осы теңсіздіктерден, I=J шығады. Қажеттілігі дәлелденді.

2. Шектелген өлшемді D жиыны бойынша жалпыланған I интегралы бар болсын. D-ны құрайтын, Р тіктөртбұрышы бойынша 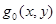функциясының I интегралының бар болатынын дәлелдеу керек. Интегралдану критерийінен, мынадай 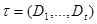табылады да, 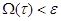аламыз.

Әрбір r=1,.. t үшін, 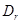жиыны өлшемді, сондықтан 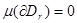. Олай болса, 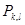тіктөртбұрышынан құрылған, мынадай қарапайым F фигурасы табыладыда, кем дегенде бір 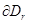, r=1,…t шекарасының нүктесін құрайтын, барлық 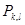қосынды ауданы 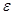-нен аспайды, яғни .

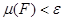F шекараның түзу сызықты кесіндісін Р тіктөртбұрышының қабырғасымен қиылысқанша созамыз. Осы тіктөртбұрыштың Т бөлінуін аламыз. P/F- қа жататын тіктөртбұрыштардың 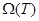омега-қосыдысына 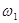кірісі, 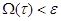-нан аспайды. F-те жататын сондай тіктөртбұрыштардың 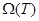-ға 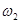кірісі 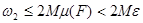-нан аспайды. Олай болса,

.

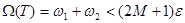Бұдан тіктөртбұрыш бойынша функцияның интегралдану критерийіне байланысты, J интегралының бар болатыны шығады. Осыған ұқсас, Дарбудың жоғарғы қосындысы үшін талқылап, мына теңсіздікті аламыз: 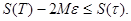Олай болса, 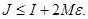Еркін түрде 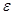оң санын таңдауымызға байланысты бұдан 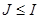-ді аламыз. Дарбудың төменгі қосындысы үшін бағалаудан қарама-қарсы 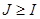теңсіздігін аламыз. Сонымен, I=J. Дәлелденді.