Замкнутые системы массового обслуживния

Задача. Автоматизированная система управления АСУ продажей железнодорожных билетов состоит из двух параллельно работающих ЭВМ. При выходе из строя одной ЭВМ АСУ продолжает нормально функционировать за счет работы другой ЭВМ. Поток отказов каждой ЭВМ простей­ший. Среднее время безотказной работы одной ЭВМ равно 10 суткам. При выходе из строя отказавшую ЭВМ начинают ремонтировать. Время ремонта ЭВМ распределено по пока­зательному закону и в среднем составляет 2 суток. В начальный момент обе ЭВМ исправны. Найти: 1) вероятность того, что обе ЭВМ исправны, 2) среднее число работающих ЭВМ, 3) среднюю производи­тельность АСУ, если при исправности хотя бы одной ЭВМ ее производительность равна 100%, а при отказе обеих ЭВМ продажа билетов производится вручную, обеспечивая 30% общей производительности АСУ.

Решение. 1) найдем вероятность того, что обе ЭВМ исправны.

Обозначим состояния АСУ по числу вышед­ших из строя ЭВМ: A₀ — обе ЭВМ исправны; А₁ — одна ис­правна, одна ремонтируется; А₂ — обе ЭВМ ремонтируются. Так как потоки отказов и восстановления ЭВМ являются про­стейшими, то их интенсивности вычисляются по формулам (14) и (16):

l = 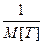= 0, 1 (отказов/сутки); m = 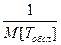=0,5 (восстановления/сутки)

Размеченный граф состояний изображен на рис. 5.

l₀ = 1/5 l₁ = 1/10

А₀ А₁ А₂

m₁ = 1/2 m₂ = 1

рис. 5

По­скольку в состоянии A₀ работают две ЭВМ, каждая из которых может отказать с интенсивностью l = 1/10, то АСУ перехо­дит из состояния а₀ в состояние А₁ с интенсивностьюl₀ =2(1/10) = 1/5; переход А₁®А₂ происходит с интенсивностью l₁ = 1/10.

Из состояния А₂ в состояние А₁ система перехо­дит с интенсивностью m₂ = 2 m = 2 (1/2) =1,так как восстанав­ливаются две ЭВМ; переход А₁® А₂ происходит с интенсив­ностью m₁ = m = 1/2. Полученный граф состояний является графом процесса гибели и размножения с числом состояний k + 1 = 3, так как k=2. Воспользуемся формулами (11) для вычисления пре­дельного распределения вероятностей

p₀ = 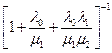= = 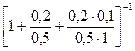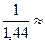0,694.

p₁ = 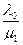p₀ = 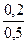0,694 » 0,278;

p₂ = 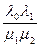p₀ = 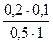0,694 » 0,028.

Вычислим p₀ + p₁ +p₂ =0,694+0,278+0,028=l, что и следова­ло ожидать, так как система может находиться только в одном из трех возможных состояний А₀,, А₁, А₂.

2) найдем среднее число работающих ЭВМ.

`m = 2 p₀ + p₁ = 2 (0,694 )+ 0,278 = 1,666

3) найдем среднюю производи­тельность АСУ.

Средняя производи­тельность АСУ в установившемся режиме составит

100% (p₀+p₁) +30%p2 = 100% (0,694+0,278) +30% • 0,028 = =98,04%.

Расчет показывает, что параллельная работа всего двух ЭВМ обеспечивает достаточно высокую (98,04% от номинальной) производительность АСУ. Следовательно, нет необходимости повышать производительность системы за счет, например, присоединения третьей ЭВМ.

51-60. Вход на станцию метрополитена оборудован системой из k турникетов.

При выходе из строя одного из турникетов остальные продолжают нормально

функционировать. Вход на станцию перекрывается, если выйдут из строя все турникеты.

Поток отказов каждого турникета - простейший, среднее время безотказной работы одного турникета t часов. При выходе из строя каждый турникет начинает сразу ремонтироваться. Время ремонта распределено по показательному закону и в среднем составляет s часов. В начальный момент все турникеты исправны. Найти среднюю пропускную способность системы турникетов в процентах от номинальной, если с выходом из строя каждого турникета система теряет (100/k)% своей номинальной пропускной способности.

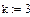
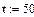
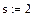
Найдем интенсивности и коэффициент r:

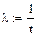
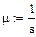
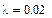
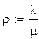
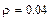
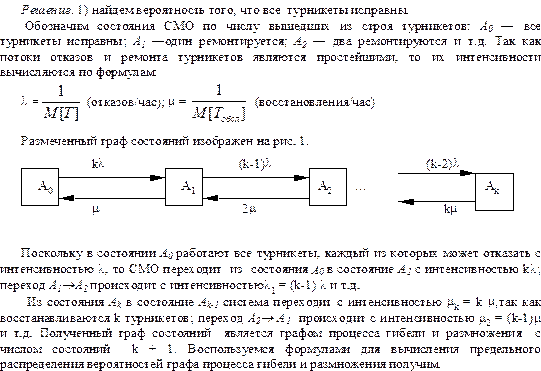
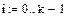
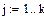
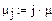
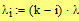
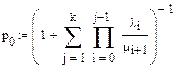
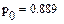
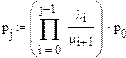
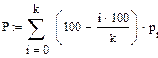
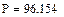
Расчет показывает, что параллельная работа 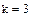турникетов обеспечивает достаточно высокую 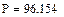пропускную способность. Следовательно, нет необходимости увеличивать количество турникетов