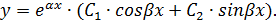Справочный материал к контрольной работе.

Решение.

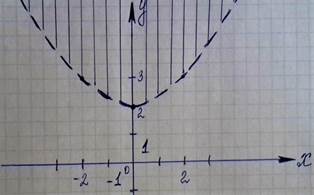
Областью определения будет являться множество пар чисел 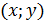, при которых выражение 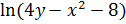определено, т.е. множество точек плоскости Oxy, для которых 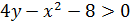или

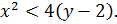
2.Найти 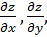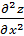, 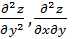от функции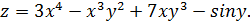

Решение.

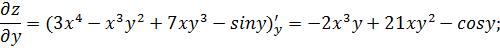
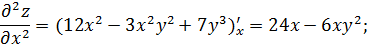
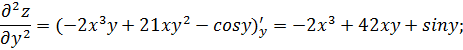
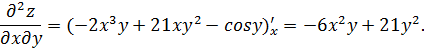
3.Найти экстремумы функции .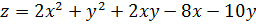

Решение.

Находим частные производные первого порядка

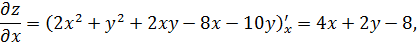
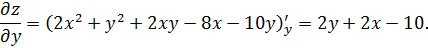
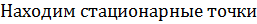
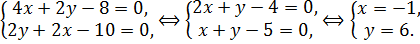
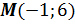– стационарная точка.

Находим частные производные второго порядка

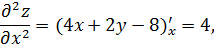
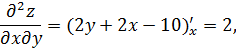
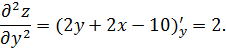
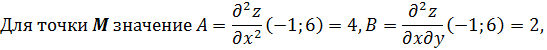
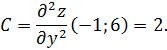
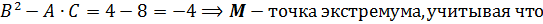
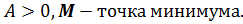
4.Вычислите .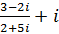

Решение.

Выполняем арифметические действия с комплексными числами учитывая, что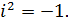

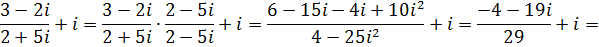
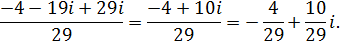
5.Найти общее решение уравнения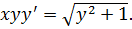

Решение. Разделим обе части уравнения на выражение 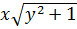(при x ≠ 0):

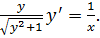Далее запишем 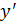как 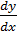и умножим обе части уравнения на dx: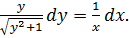

Проинтегрируем: 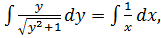интеграл от правой части является табличным, интеграл от левой части вычислим отдельно методом замены переменной.

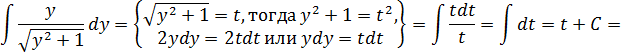
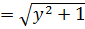+C.

В результате получим 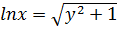+C,тогда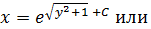

.

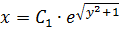Общее решение уравнения: .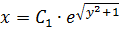

6.Решить задачу Коши: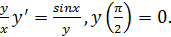

Решение. Найдем общее решение уравнения. Умножим обе части уравнения на выражение 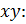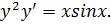Далее запишем 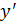как 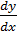и умножим обе части уравнения на dx: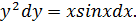

Проинтегрируем: 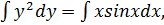интеграл от левой части является табличным, интеграл от правой части вычислим отдельно методом интегрирования по частям.

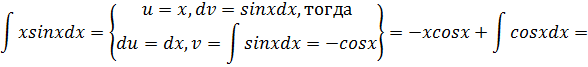
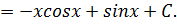
Общее решение уравнения: 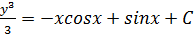или

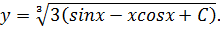
С помощью начального условия найдём значение константы интегрирования C:

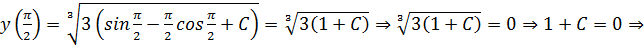
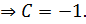
Решение задачи Коши: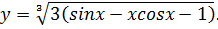

7.Решить задачу Коши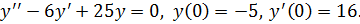

Решение. Составим характеристическое уравнение: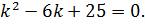

Дискриминант этого уравнения 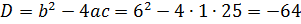отрицательный, значит существует два комплексно сопряженных корня

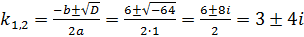, определяющих вид общего решения дифференциального уравнения:

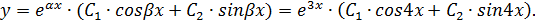
Константы интегрирования 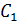и 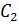найдем с помощью начальных условий:

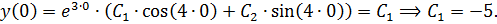
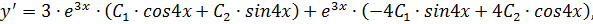
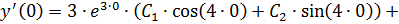
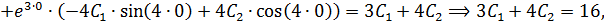
тогда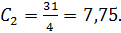

Решение задачи Коши:

.

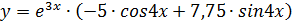Справочный материал к контрольной работе.

1.Переменнаяz называется функцией двух переменных, если каждой упорядоченной паре чисел (х, у) 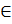D по определенному правилу f ставится в соответствие число z: z=f (x, y).

Областью определения D может быть часть плоскости x0y или вся плоскость, а областью ее значений Е – некоторый промежуток на оси zили вся ось.

2.Частной производной функции нескольких переменных по какой-нибудь из переменных в рассматриваемой точке называется обычная производная по этой переменной, при этом другие переменные считаются фиксированными, т.е. постоянными.

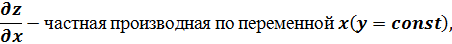
Для вычисления используются обычные правила дифференцирования и таблица производных функции одной переменной.

3.Если частные производные функции z=f (x, y) сами являются функциями переменных x, y и могут иметь соответствующие частные производные, то можно получить частные производные функции второго порядка.

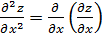– f (x, y) дифференцируется последовательно два раза по х при фиксированном значении y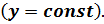

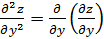- f (x, y) дифференцируется последовательно два раза по y при фиксированном значении x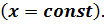

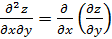– f (x, y) дифференцируется сначала по y (x = const), а потом результат – по x (y = const).

4. Необходимое условие экстремума функции f (x, y). Если точка 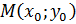-точка экстремума дифференцируемой функции f (x, y), то частные производные 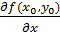и 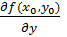одновременно равны нулю в этой точке.

Точка, в которой все частные производные 1-го порядка равны нулю, называется стационарной для данной функции.

5. Достаточные условия экстремума:
если 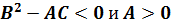, то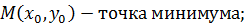
если 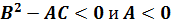, то .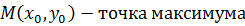

.

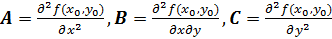6.Уравнение, связывающее независимую переменную, искомую функцию этой переменной и ее производные, называется дифференциальным уравнением.

Дифференциальное уравнение порядка n: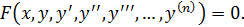

7.Общим решением дифференциального уравнения называется функция

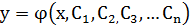, такая, что при любых фиксированных значениях 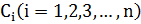она является решением данного уравнения.

8.Частным решением дифференциального уравнения называется каждое решение, получаемое из общего при конкретной совокупности значений 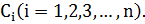Для нахождения численных значений постоянных формулируетсяn дополнительных (начальных) условий.

9.Задача о нахождении решения дифференциального уравнения порядка n, удовлетворяющего начальным условиям, называется задачей Коши.

10.Видоднородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:

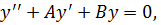где A и B постоянные числа.

Его характеристическое уравнение: (квадратное уравнение, имеющее два корня 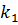и ).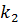

11.Общее решение однородного дифференциального уравнения 2-го порядка с постоянными коэффициентами:

a) если корни характеристического уравнения вещественные и разные ( 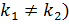, то

;

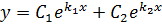b) если корни характеристического уравнения вещественные и кратные ( 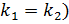, то

;

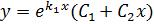c) если корни характеристического уравнения комплексные 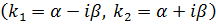, то