Преобразование неопределённостей
Правило Лопиталя применимо лишь для раскрытия неопределённостей вида 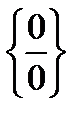 и
и 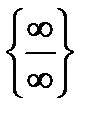 . Но некоторые функции можно преобразовать и получить неопределённость одного из этих видов:
. Но некоторые функции можно преобразовать и получить неопределённость одного из этих видов:
1) 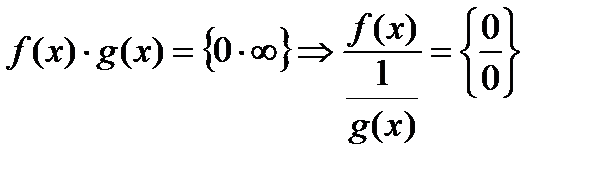 или
или 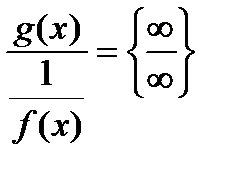 ;
;
2) 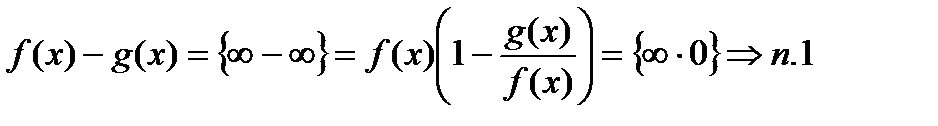 ;
;
3) 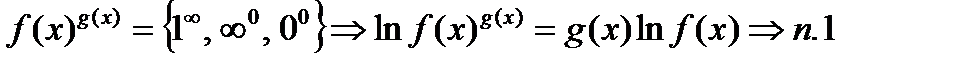
Примеры
1. Найти пределы
1) 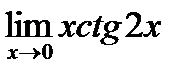 ; 2)
; 2) 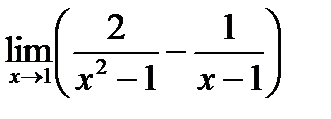 ;
;
3) 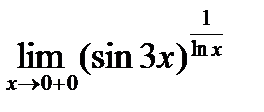 ; 4)
; 4) 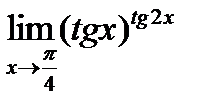 .
.
1) 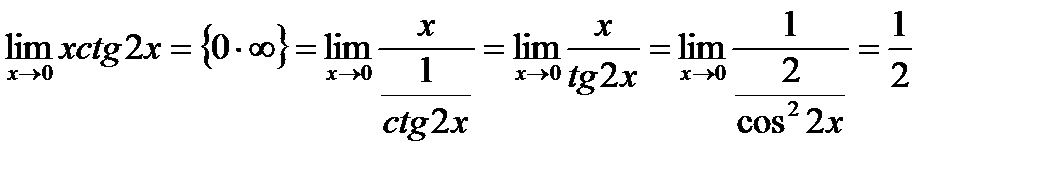 ;
;
2) 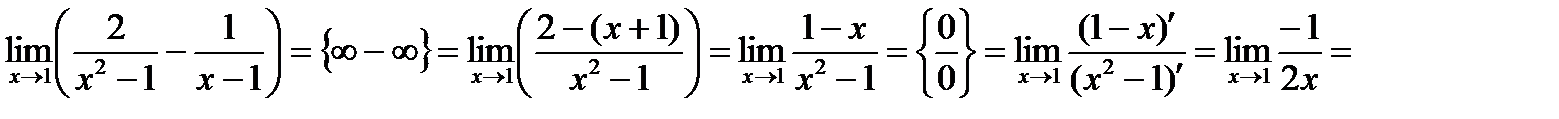
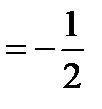 ;
;
3) этот предел содержит неопределённость вида 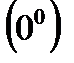 . Обозначим функцию
. Обозначим функцию 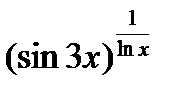 через y и прологарифмируем её:
через y и прологарифмируем её:
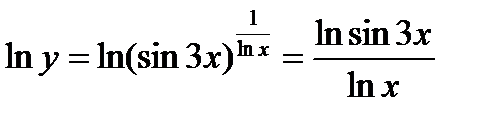 .
.
Тогда
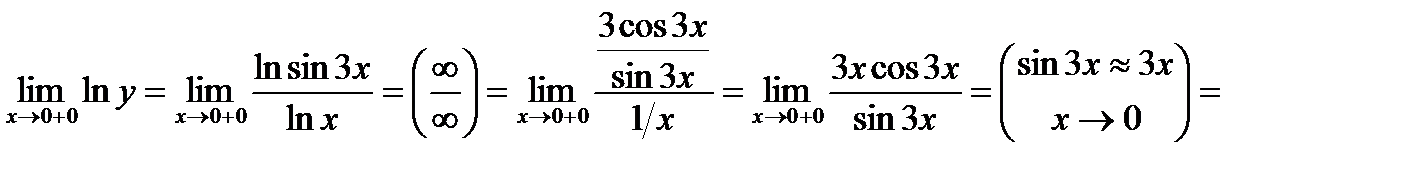
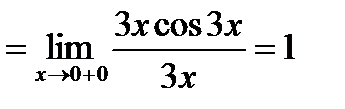 .
.
Так как 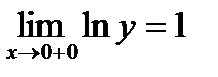 , то
, то 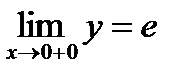 .
.
4) этот предел содержит неопределённость вида 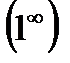 . Обозначим функцию
. Обозначим функцию 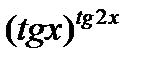 через y и прологарифмируем её:
через y и прологарифмируем её:
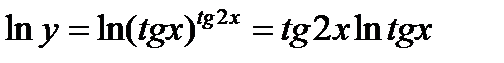 .
.
Тогда
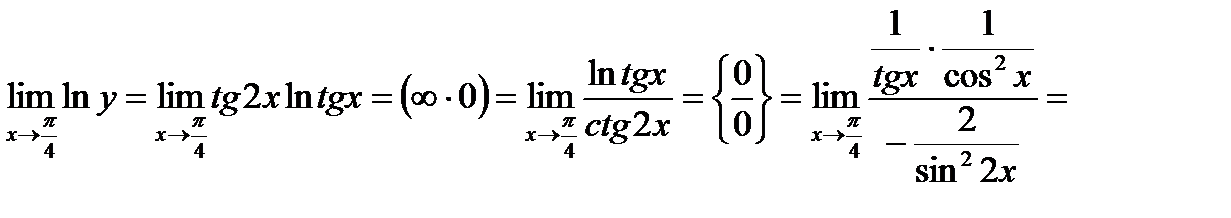
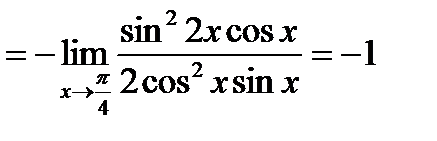 .
.
Так как 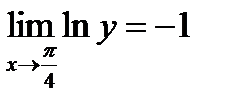 , то
, то 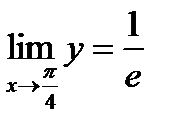 .
.
Контрольная работа №1
ЧАСТЬ 1
Задание 1.Найти решение неоднородной системы линейных уравнений
а) с помощью правила Крамера;
б) методом обратной матрицы;
в) методом Жордана-Гаусса:
1. 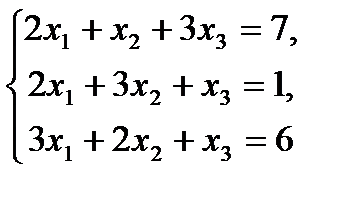 6.
6. 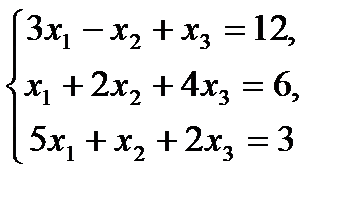
2. 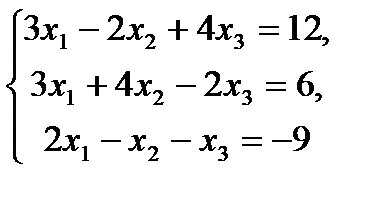 7.
7. 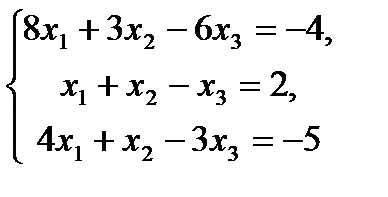
3. 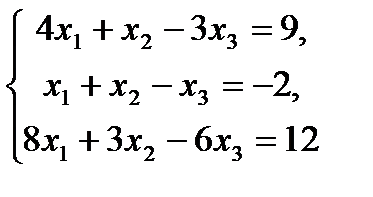 8.
8. 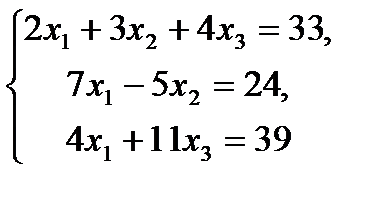
4. 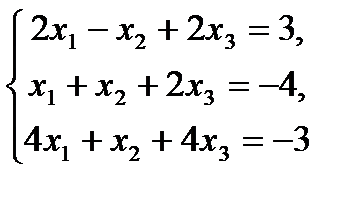 9.
9. 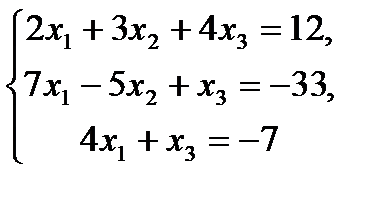
5. 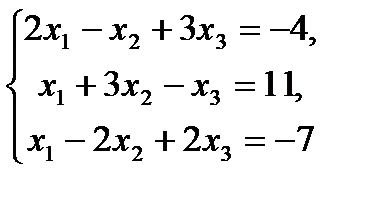 10.
10. 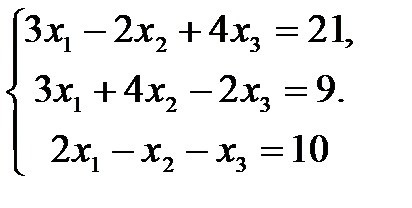
Задание 2. Решить однородную систему линейных алгебраических уравнений.
1). 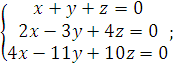 2).
2). 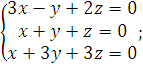
3). 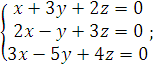 4).
4). 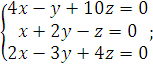
5). 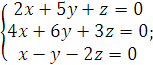 6).
6). 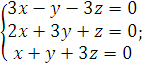
7). 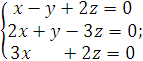 8),
8), 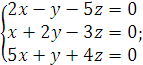
9). 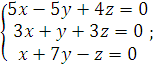 10).
10). 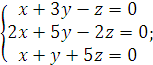
Задание 3. Решить однородную систему линейных алгебраических уравнений.
1). 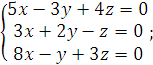 2).
2). 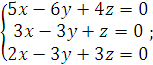
3). 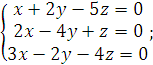 4).
4). 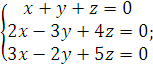
5). 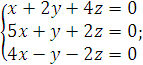 6).
6). 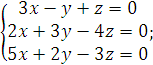
7). 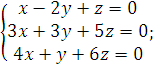 8).
8). 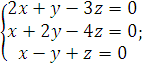
9). 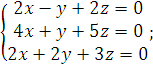 10).
10). 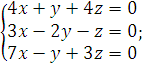
Задание 4. Даны векторы 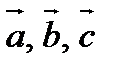 . Необходимо: а). вычислить смешанное произведение векторов
. Необходимо: а). вычислить смешанное произведение векторов 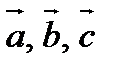 , проверить, будут ли они компланарны; б). найти модуль векторного произведения векторов
, проверить, будут ли они компланарны; б). найти модуль векторного произведения векторов 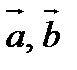 ; в). вычислить скалярное произведение векторов
; в). вычислить скалярное произведение векторов 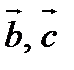 ; г). проверить, будут ли коллинеарны или ортогональны вектора
; г). проверить, будут ли коллинеарны или ортогональны вектора 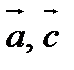 .
.
1). 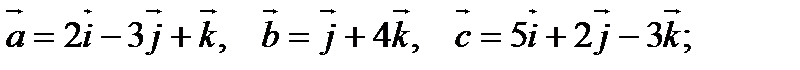
2). 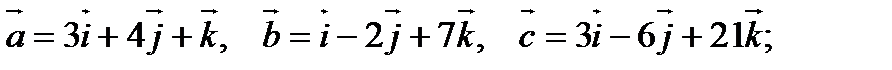
3). 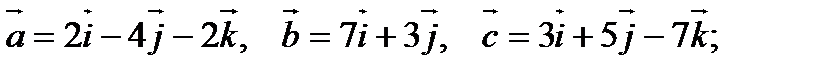
4). 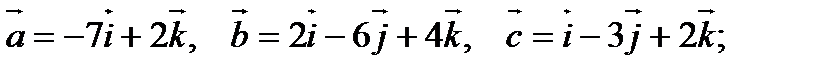
5). 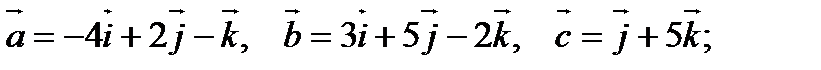
6). 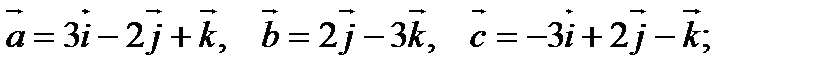
7). 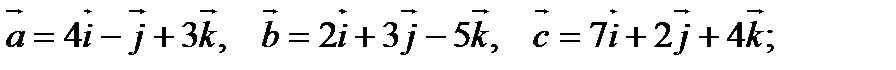
8). 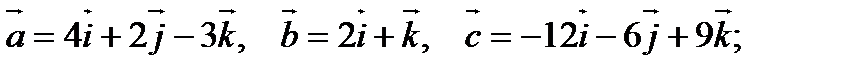
9). 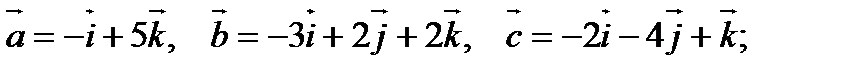
10). 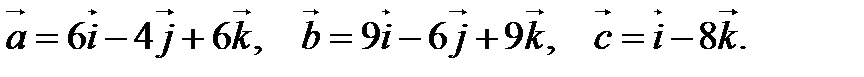
Задание 5. Вершины пирамиды находятся в точках A, B, C, и D. Вычислить: а). площадь указанной грани; б). площадь сечения, проходящего через середину ребра L и две вершины пирамиды; в). длины указанных рёбер и угол между ними; г). объём пирамиды ABCD.
1). A(5, 2, 4), B(-3, 5, -7), C(1, -5, 8), D(9, -3, 5); а). ABD; б). L=BD, А и С;
в). АВ и AC.
2). A(-7, -6, -5), B(5, 1, -3), C(8, -4, 0), D(3, 4, -7); а). BCD; б). L=AD, B и C; в). DC и DB .
3). A(3, 4, 5), B(1, 2, 1), C(-2, -3, 6), D(3, -6, -3); а). ACD; б). L=AB, C и D; в). BC и BA.
4). A(-4, -2, -3), B(2, 5, 7), C(6, 3, -1), D(6, -4, 1); а). ACD; б). L=BC, A и D; в). CA и CD.
5). A(-6, -3, -5), B(5, 1, 7), C(3, 5, -1), D(4, -2, 9); а). ACD; б). L=BC, A и D; в). AD и AC.
6). A(7, 5, 8), B(-4, -5, 3), C(2, -3, 5), D(5, 1, -4); а). BCD; б). L=BC, A и D; в). СB и CA.
7). A(7, 4, 9), B(1, -2, -3), C(-5, -3, 0), D(1, -3, 4); а). ABD; б). L=AB, C и D; в). BD и BA.
8). A(5, 3, 6), B(-3, -4, 4), C(5, -6, 8), D(4, 0, -3); а). BCD; б). L=BC, A и D; в). AC и AD.
9). A(4, 3, 1), B(2, 7, 5), C(-4, -2, 4), D(2, -3, -5); а). ACD; б). L=AB, C и D; в). DA и DC.
10). A(-5, -3, -4), B(1, 4, 6), C(3, 2, -2), D(8, -2, 4); а). ACD; б). L=BC, A и D; в). AC и AB.
Задание 6. Даны вершины треугольника ABC. Найти:
а). уравнение стороны АВ;
б). уравнение высоты CH;
в). уравнение медианы AM;
г). точку N пересечения медианы AM и высоты CH;
д). острый угол между высотой CH и медианой AM;
е). длину высоты CH.
1). 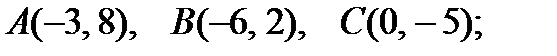
2). 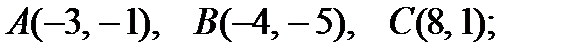
3). 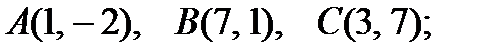
4). 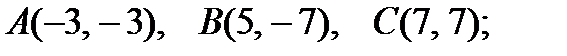
5). 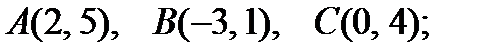
6). 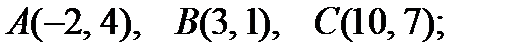
7). 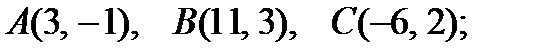
8). 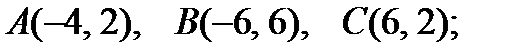
9). 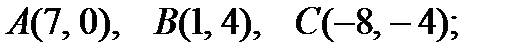
10). 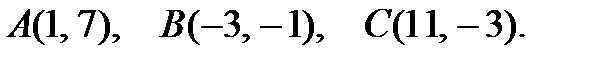
Задание 7. Даны четыре точки 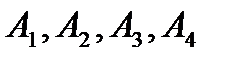 . Выяснить, лежат ли эти точки в одной плоскости. Если не лежат, сделать следующее:
. Выяснить, лежат ли эти точки в одной плоскости. Если не лежат, сделать следующее:
а). составить уравнение плоскости  ;
;
б). найти расстояние от точки 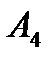 до плоскости
до плоскости 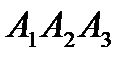 ;
;
в). написать уравнение перпендикуляра к плоскости 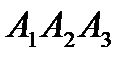 , проходящего через точку
, проходящего через точку 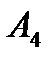 ;
;
г). найти острый угол, образованный этим перпендикуляром и прямой 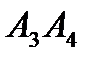 ;
;
д). вычислить синус угла между прямой 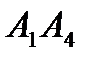 и плоскостью
и плоскостью 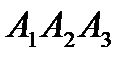 ;
;
е). вычислить косинус угла между координатной плоскостью 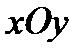 и плоскостью
и плоскостью 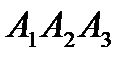 ;
;
ж). составить уравнение прямой, проходящей через точку 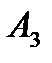 , параллельно прямой
, параллельно прямой 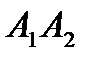 ;
;
з). составить уравнение плоскости, проходящей через точку 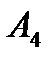 перпендикулярно к прямой
перпендикулярно к прямой 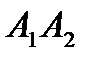 .
.
1). 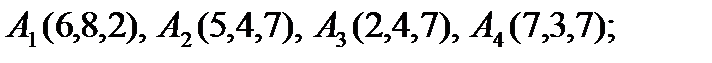
2). 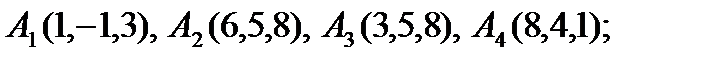
3). 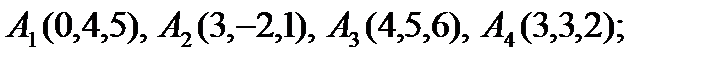
4). 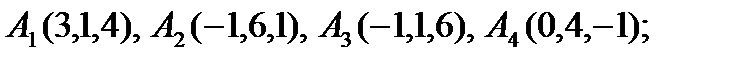
5). 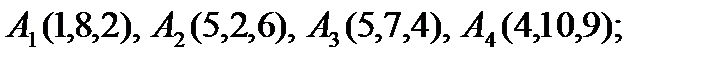
6). 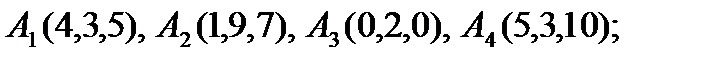
7). 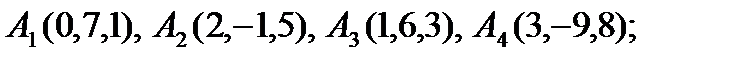
8). 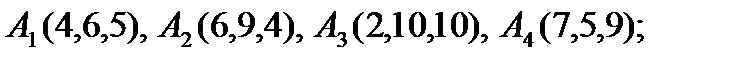
9). 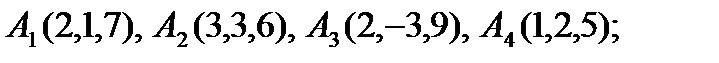
10). 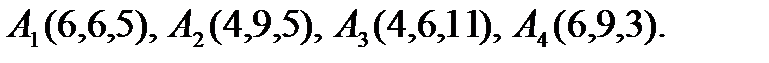
ЧАСТЬ 2
Вычислить пределы, не используя правило Лопиталя.
Задание 1
1) 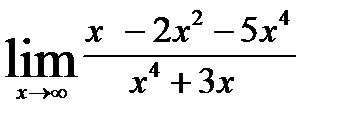 ; 6)
; 6) 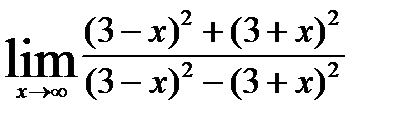 ;
;
2) 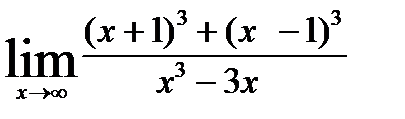 ; 7)
; 7) 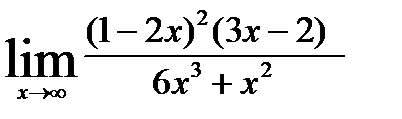 ;
;
3) 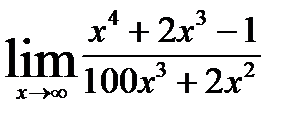 ; 8)
; 8) 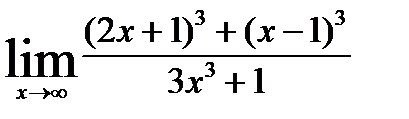 ;
;
4) 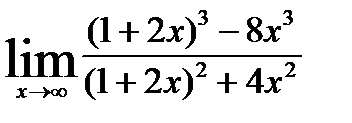 ; 9)
; 9) 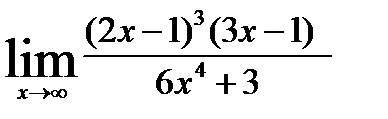 ;
;
5) 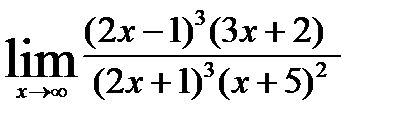 ; 10)
; 10) 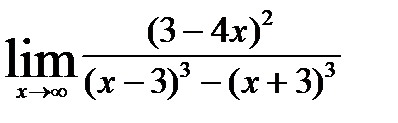 .
.
Задание 2
1) 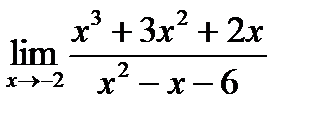 ; 6)
; 6) 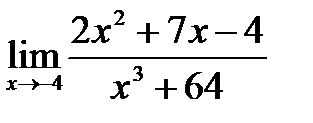 ;
;
2) 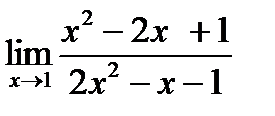 ; 7)
; 7) 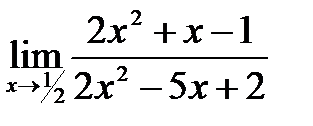 ;
;
3) 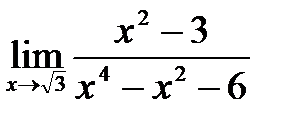 ; 8)
; 8) 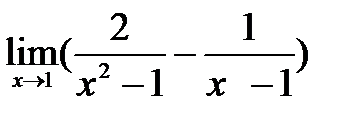 ;
;
4) 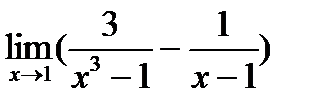 ; 9)
; 9) 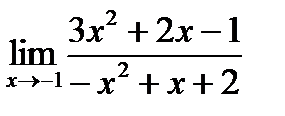 ;
;
5) 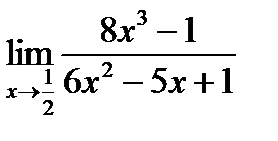 ; 10)
; 10) 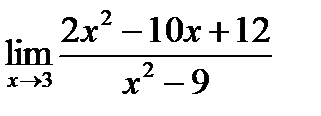 .
.
Задание 3
1) 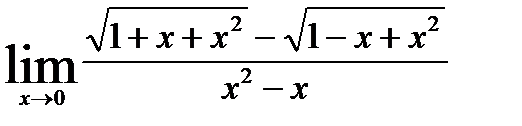 ; 3)
; 3) 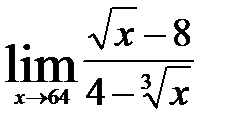 ;
;
2) 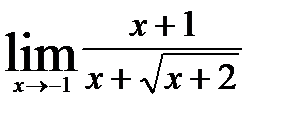 ; 4)
; 4) 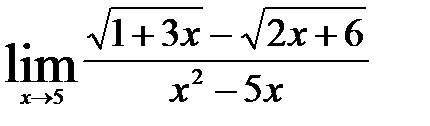 ;
;
5) 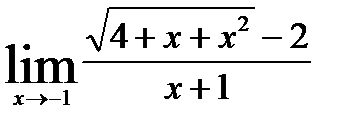 ; 8)
; 8) 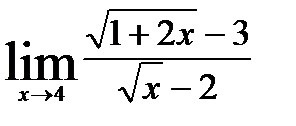 ;
;
6) 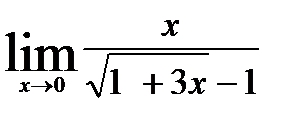 ; 9)
; 9) 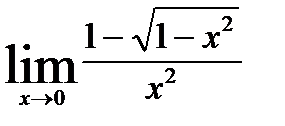 ;
;
7) 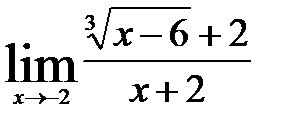 ; 10)
; 10) 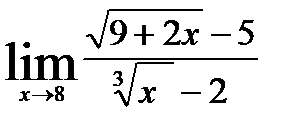 .
.
Задание 4
1) 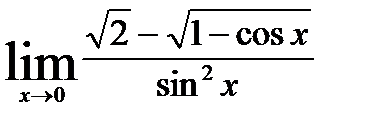 ; 6)
; 6) 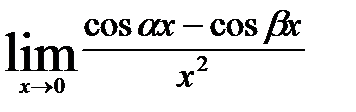 ;
;
2) 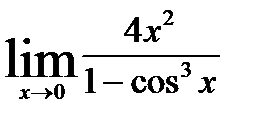 ; 7)
; 7) 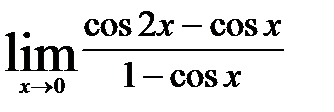 ;
;
3) 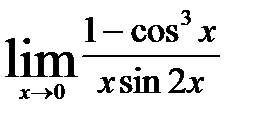 ; 8)
; 8) 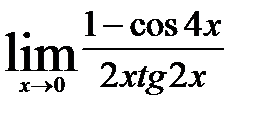 ;
;
4) 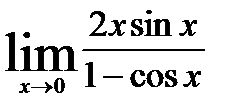 ; 9)
; 9) 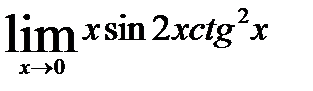 ;
;
5) 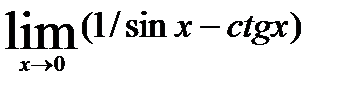 ; 10)
; 10) 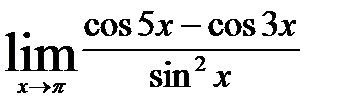 .
.
Задание 5
1) 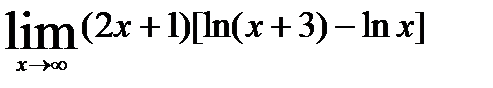 ; 6)
; 6) 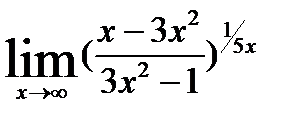 ;
;
2) 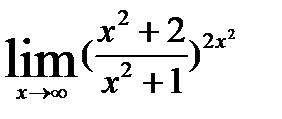 ; 7)
; 7) 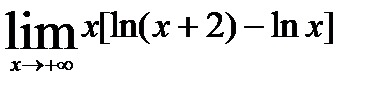 ;
;
3) 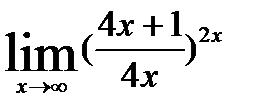 ; 8)
; 8) 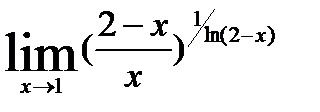 ;
;
4) 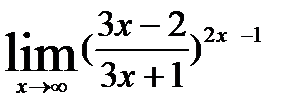 ; 9)
; 9) 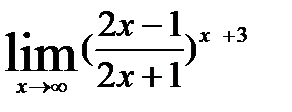 ;
;
5) 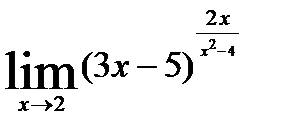 ; 10)
; 10) 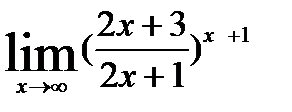 .
.
Вычислить производные:
Задание 6
1) 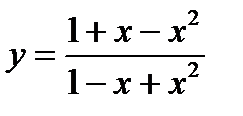 ; 6)
; 6) 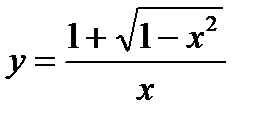 ; 2)
; 2) 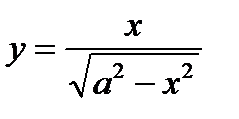 ; 7)
; 7) 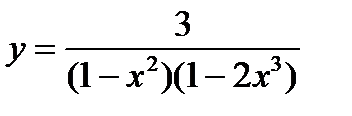 ;
;
3) 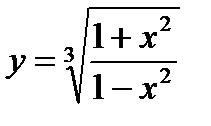 ; 8)
; 8) 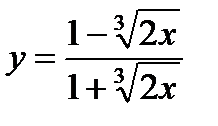 ;
;
4) 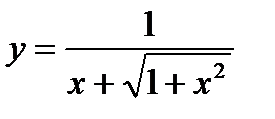 ; 9)
; 9) 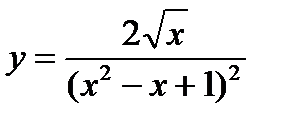 ;
;
5) 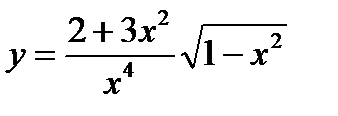 ; 10)
; 10) 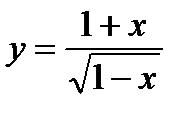 .
.
Задание 7
1) 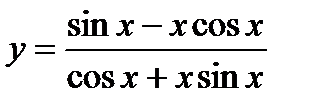 ; 6)
; 6) 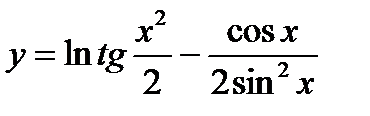 ;
;
2) 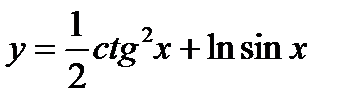 ; 7)
; 7) 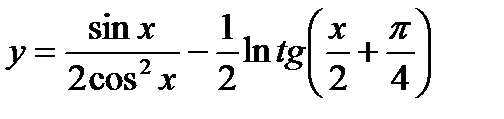 ;
;
3) 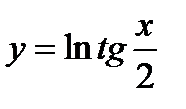 ; 8)
; 8) 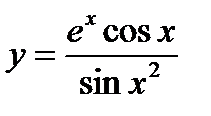 ;
;
4) 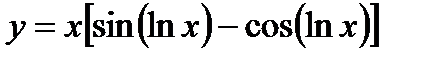 ; 9)
; 9) 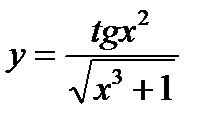 ;
;
5) 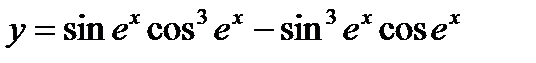 ; 10)
; 10) 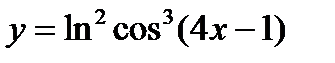 .
.
Задание 8
1) 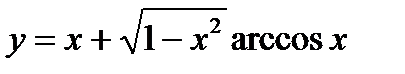 ; 6)
; 6) 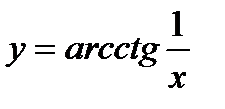 ;
;
2) 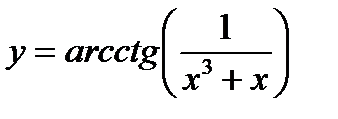 ; 7)
; 7) 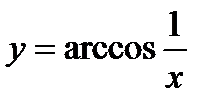 ;
;
3) 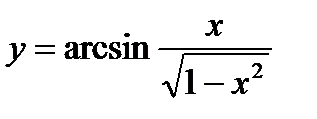 ; 8)
; 8) 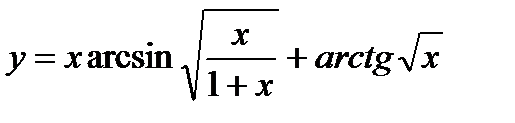 ;
;
4) 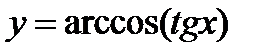 ; 9)
; 9) 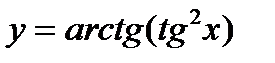 ;
;
5) 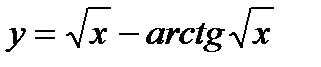 ; 10)
; 10) 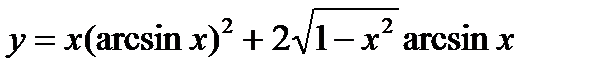 .
.
Задание 9
1) 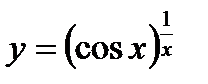 ; 6)
; 6) 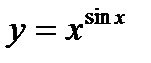 ;
;
2) 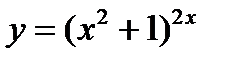 ; 7)
; 7) 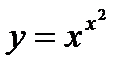 ;
;
3) 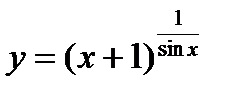 ; 8)
; 8) 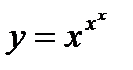 ;
;
4) 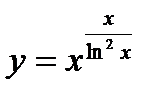 ; 9)
; 9) 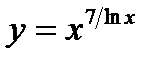 ;
;
5) 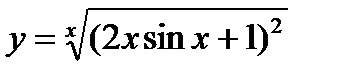 ; 10)
; 10) 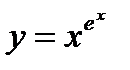 .
.
Задание 10
1) 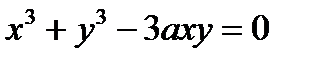 ; 6)
; 6) 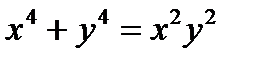 ;
;
2) 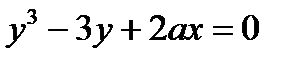 ; 7)
; 7) 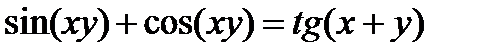 ;
;
3) 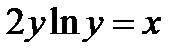 ; 8)
; 8) 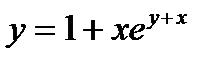 ;
;
4) 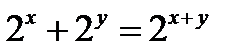 ; 9)
; 9) 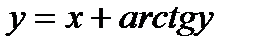 ;
;
5) 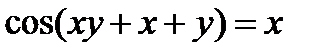 ; 10)
; 10) 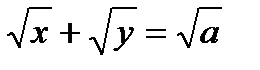 .
.
Задание 11
Вычислить производные первого порядка:
1) 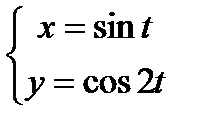 ; 3)
; 3) 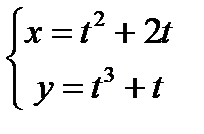 ;
;
2) 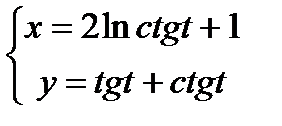 ; 4)
; 4) 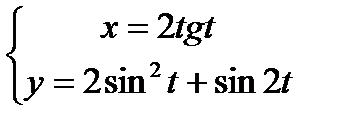 ;
;
5) 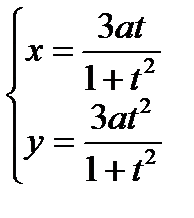 ; 8)
; 8) 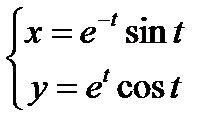 ;
;
6) 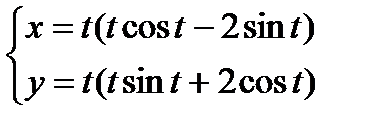 ; 9)
; 9) 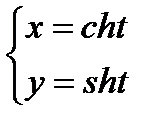 ;
;
7) 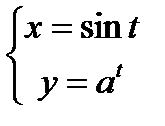 ; 10)
; 10) 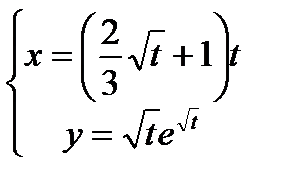 .
.
Вычислить пределы с использованием правила Лопиталя:
Задание 12
1) 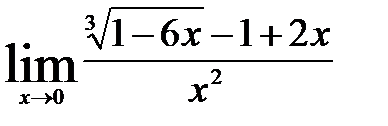 ; 6)
; 6) 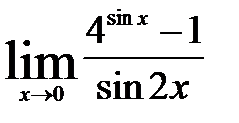 ;
;
2) 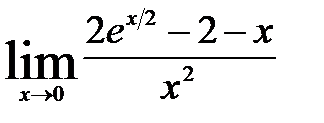 ; 7)
; 7) 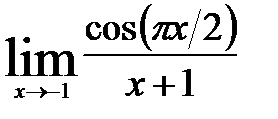 ;
;
3) 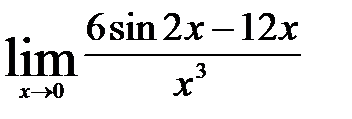 ; 8)
; 8) 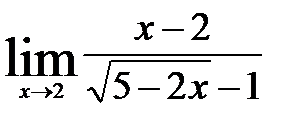 ;
;
4) 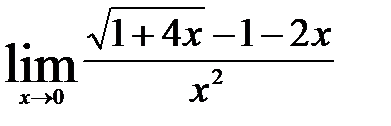 ; 9)
; 9) 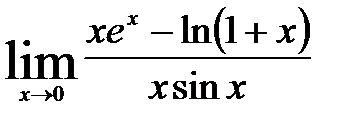 ;
;
5) 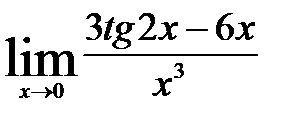 ; 10)
; 10) 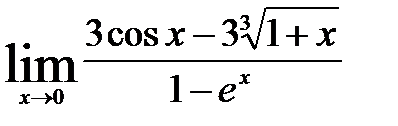 .
.
Задание 13
1) 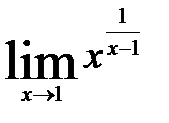 ; 4)
; 4) 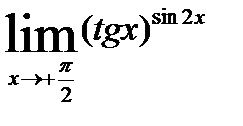 ;
;
2) 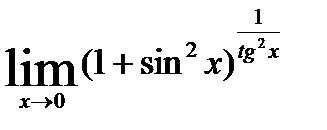 ; 5)
; 5) 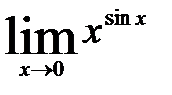 ;
;
3) 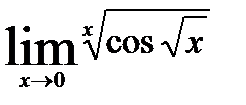 ; 6)
; 6) 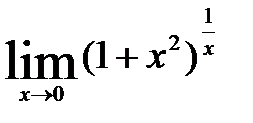 ;
;
7) 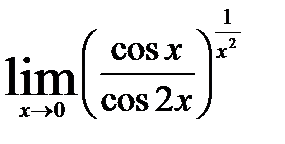 ; 9)
; 9) 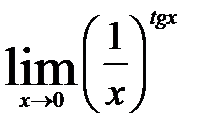 ;
;
8) 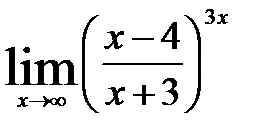 ; 10)
; 10) 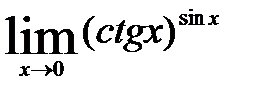 .
.
Литература
1. Пискунов Н.С. Дифференциальное и интегральное исчисления, т.1
2. Шнейдер В.Е. и др. Краткий курс высшей математики, т.1
3. Минорский В.П. Сборник задач по высшей математике.
4. Данко П.Е. Высшая математика в упражнениях и задачах. Часть 1.
5. Рябушко А.П. Сборник индивидуальных заданий по высшей математике, т.1.
6. Запорожец Г.И. Руководство к решению задач по математическому анализу.
Программа к экзамену
Матрицы и определители (общие понятия). Прямоугольная, квадратная, единичная, транспонированная матрица. Свойства определителей. Алгебраические дополнения и миноры. Разложение определителя по строке (столбцу).
Операции над матрицами. Линейные операции, умножение матриц. Невырожденная, обратная матрица. Элементарные преобразования матрицы. Ранг матрицы. Нахождение обратной матрицы. Определение ранга.
Системы линейных уравнений. Однородная и неоднородная система линейных алгебраических уравнений. Совместная система. Теорема Кронекера-Капелли. Фундаментальная система решений, общее решение. Методы решения: правило Крамера, метод Гаусса.
Векторы (общие понятия). Определение вектора. Равенство, коллинеарность, компланарность векторов. Длина вектора. Проекция вектора на ось. Сложение векторов и умножение вектора на число. Линейные операции над векторами. Базис на плоскости и в пространстве. Линейная зависимость векторов. Разложение вектора по базису. Прямоугольные координаты и направляющие косинусы вектора
Умножение векторов. Скалярное, векторное и смешанное произведения векторов, их свойства, геометрический смысл, выражение через координаты сомножителей. Угол между векторами, условия их ортогональности, коллинеарности и компланарности.
Прямая линия. Уравнение прямой на плоскости, его различные формы. Расстояние от точки до прямой. Углы между прямыми, условия их параллельности, ортогональности.
Плоскость. Уравнения плоскости и прямой в пространстве. Расстояние от точки до плоскости. Углы между плоскостями, прямой и плоскостью, условия их параллельности, ортогональности.
Кривые второго порядка. Уравнения и свойства кривых второго порядка на плоскости:окружности, эллипса, гиперболы, параболы.
Предел функции одной переменной. Предел функции в точке. Свойства сходящихся функций. Односторонние пределы. Первый и второй замечательные пределы.
Непрерывность функции. Непрерывность в точке и на отрезке. Точки разрыва функции.
Производная функции. Приращение функции и аргумента. Геометрический и механический смысл производной (задачи о касательной и скорости). Дифференцируемость функции. Производные высших порядков.
Правила дифференцирования. Производная суммы, произведения и отношения функций. Дифференцирование сложной, параметрически заданной и обратной функций.
Раскрытие неопределенностей. Применение производных для нахождения пределов неопределенных выражений. Первое и второе правила Лопиталя.
Локальный экстремум, наибольшее и наименьшее значения функции. Необходимые и достаточные условия существования экстремума. Схема нахождения экстремумов, наибольшего и наименьшего значения функции.
Построение графика функции. Определение экстремумов, областей монотонности, выпуклости и вогнутости кривой, точек перегиба. Правило нахождения асимптот графика функции. Общая схема построения графика.
