Кратчайшие пути с фиксированными платежами

Все задачи о нахождении кратчайшего пути между двумя фиксированными вершинами исходили из следующего предположения: если кратчайший путь от s до t проходит через вершину k, то его отрезок от s до k будет кратчайшим путем от s до k и отрезок от k до t будет кратчайшим путем от k до t. Существует класс задач, для которых это не так. Это задачи с фиксированными платежами. Подобные задачи возникают в том случае, если за прохождение вершины сети взимается плата. Решаются такие задачи довольно сложно, но есть один класс транспортных задач, которые сводятся к уже рассмотренным нами задачам.

ЗАДАЧА О ШТРАФАХ ЗА ПОВОРОТЫ

УСЛОВИЕ. Имеется сеть улиц с односторонним или двусторонним движением. В качестве модельного графа рассмотрим сеть улиц с односторонним движением (рис. 10.8). Дугам приписаны неотрицательные числа, представляющие собой плату или время проезда. При выполнении поворота вводится некая фиксированная плата – задержка или штраф (неотрицательное число). Этот штраф зависит от направления движения при въезде и выезде. За выполнение запрещенного поворота взимается бесконечно большой штраф. Для для модельного графа будем считать, что за выполнение каждого поворота взимается штраф, равный 3.

ВОПРОС. Найти минимальный путь из s=1 в t=8.

ТЕОРЕМА

В сети со штрафами за повороты кратчайший путь из s в t, проходящий через k, не обязан содержать кратчайшие пути от s до k и от k до t.

Для модельного примера:

1-2-3-4-8 – кратчайший путь со стоимостью 15.

1-2-3-4 – путь со стоимостью 11.

1-2-6-5-4 – кратчайший путь со стоимостью 10.

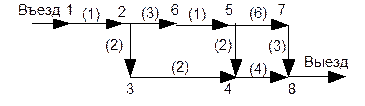
Рис. 10.8. Модельный граф

Мы уже умеем находить кратчайшие пути в задачах, где стоимости приписаны только дугам. Следовательно, по исходной сети нужно построить новую фиктивную сеть, где бы штрафы за повороты включились бы в стоимость дуг. Затем в фиктивной сети найти кратчайший путь и по нему восстановить кратчайший путь в исходной сети.

АЛГОРИТМ {Кратчайший путь со штрафами за повороты}

Шаг 1

Ввести фиктивный источник s₀ и соединить его дугой с источником s. Ввести фиктивный сток t₀ и соединить его дугой со стоком t. Стоимости фиктивных дуг положить равными 0 и считать, что повороты из фиктивных вершин никогда не выполняются.

Шаг 2

Каждой i-й дуге расширенной сети, полученной на шаге 1, приписать имя L_i. Если исходная сеть содержала m дуг, то дугам будут приписаны имена L₀,L₁,…,L_m+1 (рис. 10.9).

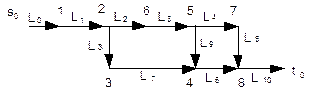
Рис. 10.9. Нумерация дуг

Шаг 3

Построение фиктивной сети (рис. 10.10).

Каждой дуге расширенной сети будет соответствовать вершина фиктивной. Две вершины фиктивной сети L_i и L_j соединены дугой только в том случае, если в исходной сети конец дуги L_i был бы началом дуги L_j. Стоимость такой дуги определяется по следующей формуле:

A(L_i)+P(L_i,L_j),где A(L_i) – стоимость дуги L_i,

P(L_i,L_j) – штраф за выполнение поворота.

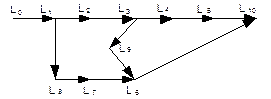
Рис. 10.10. Фиктивная сеть

Стоимости дуг фиктивной сети (рис.10.10):

L0–L1	L1–L2	L1–L8	L8–L7	L2–L3	L3–L9	L9–L6	L3–L4	L4–L5	L5–L10	L6–L10	L7–L6

Вопрос 1. Почему стоимость дуги L₅→L₁₀ равна 3, а не 6 (стоимость дуги + штраф за поворот)?

Шаг 4

Используя алгоритм Дейкстры, определить в фиктивной сети кратчайший путь.

Шаг 5

По кратчайшему пути в фиктивной сети восстановить путь в исходной: вершина фиктивной сети→дуга исходной→начало дуги.

Возникает вопрос, каким образом, зная две дуги, определить плату за поворот. В нашей задаче улицы имеют только два направления: горизонтальное и вертикальное. Будем хранить информацию о направлении каждой дуги в двумерном массиве BIN. Если BIN[i,j]=0, то дуга (i→j) имеет горизонтальное направление, если 1, то вертикальное. Рассмотрим сумму BIN[i,j] + BIN[j,k], производя сложение по mod 2. Если поворот происходит, то эта сумма равна 0+1 или 1+0, т.е. 1. Если поворот не происходит, то эта сумма равна 0+0 или 1+1, т.е. 0.

Вопрос 2. Как хранить информацию о поворотах в случае двустороннего движения?

Подсчитаем вычислительную сложность алгоритма.

Построение фиктивной сети можно выполнить за O(n²) шагов. Если соответствие дуг исходной сети вершинам фиктивной записать в специальный массив размерности 2(m+2), то восстановление пути пропорционально его длине, т.е. O(n). Вычислительная сложность алгоритма Дейкстры – O(n²). Окончательно, вычислитель­ная сложность равна O(n²).

Ответ 1. В фиктивную вершину поворот не производится.

Ответ 2. Кодировать возможные направления числами: 0, 1, 2, 3.

10.6. Первые K кратчайших путей

При решении практических задач часто бывает недостаточно знать один самый короткий путь. Будем искать первые K кратчайших путей между парой фиксированных вершин s и t, расположенных в порядке возрастания длин и не содержащих контуров. Граф, как обычно, не должен содержать контуры отрицательного веса.

Вопрос. В каком случае первые K кратчайших путей могут быть найдены уже рассмотренными нами методами?

Основная идея алгоритма – поиск отклонений от уже найденных кратчайших путей.

Пусть мы уже нашли первые j путей (j<K). Обозначим их P¹, P²,…, P^j. Найдем j+1 кратчайший путь. Рассмотрим последний найденный путь P^j = <s, 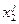, …, , 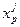t>.

Зафиксируем какую-нибудь вершину этого пути, не равную t. Пусть это будет i-я вершина 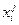(вершина s имеет номер 1). Будем искать отклонение 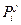в этой вершине. 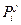устроено так: от s до 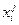оно совпадает с P^j, затем от 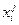до t идет по кратчайшему пути с учетом некоторых запретов (рис. 10.11).

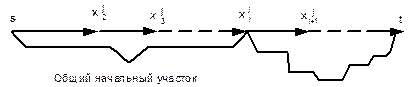
Рис. 10.11. Общий начальный участок

Запреты нужны для того, чтобы, во-первых, не сгенерировать путь, содержащий цикл; во-вторых, не сгенерировать уже найденный путь. Для этого:

1. Запретим использовать вершины s, 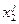, …, 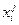при поиске кратчайшего пути от 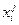до t.

2. Сравним все уже найденные пути P¹, P², …, P^j-1 с путем P^j. Выберем из них те, у которых начальный участок из i вершин <s, 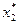, …, 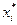> совпадает с начальным участком j-го пути <s, 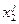,… , 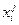>. Чтобы не сгенерировать в качестве отклонения один из этих путей, запретим использовать дуги 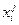→ 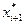в каждом из этих путей. Для этого в матрицу стоимостей A для всех таких дуг запишем A[ 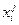, 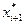]= +¥. Также запретим использование дуги 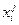→ 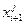: A[ , ]= +¥.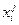

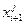С учетом этих запретов можно найти отклонение 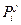, найдя кратчайший путь от 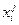до t алгоритмом Форда – Беллмана или Дейкстры (если в графе все дуги имеют неотрицательные стоимости). Таким образом будет найдено отклонение от пути P^j в i-й вершине.

Уже найденные кратчайшие пути будем хранить в окончательном списке L₀, отклонения от кратчайших путей – в рабочем списке L. Поместим в L отклонения от кратчайшего пути P^j во всех вершинах. Минимальный путь из списка L переместим в список L₀. Этот путь и будет j+1-м кратчайшим путем.

АЛГОРИТМ Йена

Шаг 1

Положить j=1. С помощью алгоритма Форда-Беллмана или Дейкстры найти кратчайший путь от s до t и поместить его в L₀.

Шаг 2

Для всех вершин 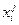(кроме последней)j-го кратчайшего пути найти отклонения и поместить их в список L. Для этого выполнить шаги 3-5. Положить i=1.

Шаг 3

Наложить запрет на использование вершин s, Проверить все пути из списков L₀ и L и выбрать пути с начальным участком, равным s, Для всех таких путей наложить запрет на использование ребра 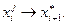Для этого в матрицу весов записать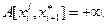

Шаг 4

С помощью алгоритма Форда – Беллмана или Дейкстры найти кратчайший путь от 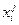до t. Добавить к нему начальный участок s, Полученный путь поместить в список L.

Шаг 5

Восстановить матрицу весов A и допустимость вершин s, Положить i=i+1. Если 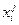не равна t, то переход к шагу 3; иначе – переход к шагу 6.

Шаг 6

Все отклонения от j-го пути уже помещены в список L. Положить j=j+1. Если L пуст, то останов; иначе – найти в L минимальный путь и перенести его в список L₀. Если j=K, то останов; иначе – переход к шагу 2.

Подсчитаем вычислительную сложность алгоритма Йена и оценим размерность рабочих списков L₀ и L.

Для каждого из первых K-1 путей ищем отклонения во всех вершинах. Вершин в пути не более n, поиск отклонения для одной вершины O(n³) или O(n²). Окончательно, вычислительная сложность равна O(Kn⁴) или O(Kn³) для неотрицательных весов.

Длина каждого пути не превосходит n (пути не содержат контуров). Количество путей в списке L₀ не превосходит K; количество путей в списке L не превосходит числа отклонений (во всех вершинах, кроме последней) для K-1 пути, т.е. (K-1)(n-1).

Пути можно хранить в виде массивов, но наиболее экономными способами являются динамическая структура «связанный список» для пути и «списки инцидентности» – для списков L₀ и L.

Ответ. Если в графе имеется не менее K различных путей одной и той же минимальной длины.

ПРИЛОЖЕНИЕ

СПИСОК NP – ПОЛНЫХ ЗАДАЧ

Данный список NP-полных задач хоть и не претендует на полноту, но может дать некоторое представление о подобных задачах, возникающих в различных областях математики и информатики.

Каждая из таких задач допускает две возможных постановки:

1) задача оптимизации;

2) задача распознавания.

В качестве примера рассмотрим задачу о коммивояжере.

Оптимизационная постановка выглядит так:

УСЛОВИЕ. Заданы конечное множество C городов, целые положительные расстояния d(c₁,c₂) для каждой пары городов c₁, c₂.

ВОПРОС ОПТИМИЗАЦИИ. Найти маршрут минимальной длины, проходящий через все города и возвращающийся в исходный пункт.

Чтобы получить теперь задачу распознавания, введем дополнительный параметр – числовую границу B.

ВОПРОС РАСПОЗНАВАНИЯ. Существует ли маршрут, проходящий через все города, длина которого не превосходит B, где B – целое положительное число? (Если решается задача на максимум, то условие «не превосходит B» заменяется условием «не меньше B».)

Традиционно к NP-полным задачам относятся задачи распознавания, однако соответствующие им задачи оптимизации эквивалентны им по сложности, поэтому при формулировке задач можно использовать любую постановку.

1. РАСКРАШИВАЕМОСТЬ ГРАФА (ХРОМАТИЧЕСКОЕ ЧИСЛО)

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|, где |V| – число вершин графа.

ВОПРОС. Верно ли, что граф K–раскрашиваем? (Граф называется K–раскрашиваемым, если его вершины можно раскрасить в K цветов так, чтобы любые две соседние вершины были окрашены в различные цвета).

2. КЛИКА

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|.

ВОПРОС. Верно ли, что граф G содержит клику размера не менее K?

(Существует ли подграф графа G такой, что число вершин в нем не меньше K и любые две вершины соединены ребром?)

3. ВЕРШИННОЕ ПОКРЫТИЕ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|.

ВОПРОС. Имеется ли в графе вершинное покрытие не более чем из K элементов? (Имеется ли такое подмножество вершин V' V мощности не более K, что для любого ребра (u–v) Є V хотя бы одна из вершин u, v принадлежит V'?)

4. РАЗБИЕНИЕ

УСЛОВИЕ. Заданы конечное множество A и положительный целый вес w(a) для каждого a Є A.

ВОПРОС. Существует ли подмножество A' A такое, что суммарный вес элементов, принадлежащих A', равен суммарному весу элементов, не принадлежащих A'? (Иными словами, можно ли A разбить на два подмножества, равные по весу?)

5. РЮКЗАК

УСЛОВИЕ. Задано конечное множество A, положительные целые веса w(a), стоимости s(a) для каждого a Є A и общее ограничение на вес K.

ВОПРОС. Найти из всевозможных выборок A' A такую, чтобы суммарный вес входящих в него элементов не превосходил K, а суммарная стоимость была максимальна.

6. РЮКЗАК С КРАТНЫМ ВЫБОРОМ ЭЛЕМЕНТОВ

УСЛОВИЕ. Задано конечное множество A, положительные целые веса w(a), стоимости s(a) для каждого a Є A, общее ограничение на вес K и минимальная стоимость B.

ВОПРОС. Можно ли так сопоставить каждому элементу a Є A целое число c(a) (кратность), чтобы суммарный вес всех предметов из A с учетом кратностей не превосходил K, а суммарная стоимость тех же предметов была не меньше B?

7. УПАКОВКА В КОНТЕЙНЕРЫ

УСЛОВИЕ. Заданы конечное множество A и размеры s(a) Є [0, 1] каждого предмета.

ВОПРОС. Найти такое разбиение множества A на непересекающиеся A₁, A₂, …, A_k, чтобы сумма размеров предметов в каждом A_i не превосходила 1 и k было минимальным.

8. ДИНАМИЧЕСКОЕ РАСПРЕДЕЛЕНИЕ ПАМЯТИ

УСЛОВИЕ. Заданы множество элементов данных A, целые положительные s(a) – размер каждого элемента, r(a) – время его поступления, d(a) – время его жизни, положительное целое число D – размер области памяти.

ВОПРОС. Существует ли для множества данных A допустимое распределение памяти? Иными словами, существует ли такая функция : A ® {1, 2, …, D}, что для каждого элемента a Є A интервал ((a), (a)+s(a)–1) – место, занимаемое им в динамической памяти, содержался бы в [1, D] и в любой фиксированный момент времени t₀ интервалы для данных с r(a) t₀ r(a)+d(a) не пересекались?

9. МНОЖЕСТВО ПРЕДСТАВИТЕЛЕЙ

УСЛОВИЕ. Задано семейство C подмножеств множества S, положительное целое число K.

ВОПРОС. Содержит ли S множество представителей для C, т.е. существует ли в S подмножество S' мощности не более K такое, что S' содержит, по крайней мере, один элемент из каждого множества семейства C.

10. УПОРЯДОЧЕНИЕ ВНУТРИ ИНТЕРВАЛОВ

УСЛОВИЕ. Задано конечное множество заданий T и для каждого задания t Є T целое число r(t) 0 – время готовности, целые положительные d(t) и l(t) – директивный срок и длительность.

ВОПРОС. Существует ли для T допустимое расписание, т.е. функция : T ® N (N – множество натуральных чисел), сопоставляющая заданию t момент начала его выполнения (t)? (Иными словами, задание t выполняется с момента времени (t) до (t)+l(t), оно не может быть начато ранее момента r(t), должно быть закончено не позднее d(t), и временной интервал выполнения одного задания не может перекрываться с интервалом другого).

11. МИНИМИЗАЦИЯ ШТРАФА ЗА НЕВЫПОЛНЕНИЕ ЗАДАНИЙ

УСЛОВИЕ. Задано конечное множество заданий T и для каждого задания t Є T целые положительные d(t) – директивный срок, l(t) – длительность и w(t) – вес, а также целое положительное число K.

ВОПРОС. Существует ли для T однопроцессорное расписание такое, что сумма 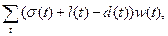взятая по тем t Є T, для которых 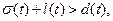не превосходит K? (Однопроцессорное расписание – это функция : T ® N (N – множество натуральных чисел), сопоставляющая заданию t момент начала его выполнения (t) такое, что задание t выполняется с момента времени (t) до (t)+l(t), оно должно быть закончено не позднее d(t), и временной интервал выполнения одного задания не может перекрываться с интервалом другого).

12. МИНИМАКСНОЕ МНОЖЕСТВО ЦЕНТРОВ

УСЛОВИЕ. Заданы граф G=<V, E> , положительный целый вес w(v) каждой вершины v Є V, положительная целая длина l(e) каждого ребра e Є E; положительное целое число K |V| и положительное рациональное число B.

ВОПРОС. Существует ли такое множество P мощности K «точек на G» (точка на G либо вершина графа, либо точка на ребре, где ребро e рассматривается как прямолинейный отрезок длины l(e)), что если d(v) – длина кратчайшего пути от вершины v до ближайшей к ней точке из P, то ?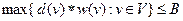

P.S. Вариант этой задачи, в котором P – подмножество вершин, также NP-полон, но если K фиксировано или G – дерево, то разрешим за полиномиальное время.

13. МНОЖЕСТВО ЦЕНТРОВ С МИНИМАКСНОЙ СУММОЙ

УСЛОВИЕ. Заданы граф G=<V, E> , положительный целый вес w(v) каждой вершины v Є V, положительная целая длина l(e) каждого ребра e Є E; положительное целое число K |V| и положительное рациональное число B.

ВОПРОС. Существует ли такое множество P мощности K «точек на G» (точка на G либо вершина графа, либо точка на ребре, где ребро e рассматривается как прямолинейный отрезок длины l(e)), что если d(v) – длина кратчайшего пути от вершины v до ближайшей к ней точке из P, то ?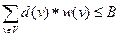

P.S. Вариант этой задачи, в котором P – подмножество вершин, также NP-полон, но если K фиксировано или G – дерево, то разрешим за полиномиальное время.

14. СКОПЛЕНИЯ

УСЛОВИЕ. Заданы конечное множество X, целые положительныерасстояния d(x,y) для каждой пары x,y элементов из X, целые положительные K и B.

ВОПРОС. Существует ли такое разбиение множества X на непересекающиеся X₁, X₂, …, X_k, что для всех x, yÎ X_i d(x,y) £ B при 1 £ i £ k?.

15. СОСТАВЛЕНИЕ УЧЕБНОГО РАСПИСАНИЯ

УСЛОВИЕ. Заданы множество H рабочих часов, множество C преподавателей, множество T учебных дисциплин, для каждого преподавателя c дано подмножество A(c) из H, называемое «допустимыми часами преподавателя c», для каждой дисциплины t подмножество A(t) множества H, называемое «допустимыми часами дисциплины t», и для каждой пары (c,t) Є CT целое положительное число R(c,t), называемое «требуемой нагрузкой».

ВОПРОС. Существует ли учебное расписание, обслуживающее все дисциплины? Иными словами, существует ли функция f: CTH ® {0,1} (где f(c,t,h)=1 означает, что преподаватель c занимается дисциплиной t в момент h), удовлетворяющая следующим условиям:

1) f(c,t,h)=1 только тогда, когда h Є пересечению A(c) и A(t);

2) для каждого h Є H и c Є C существует не более одного t Є T такого, что f(c,t,h)=1;

3) для каждого h Є H и t Є T существует не более одного c Є C такого, что f(c, t, h)=1;

4) для каждой пары (c,t) Є CT существует ровно R(c,t) значений h, для которых f(c,t,h)=1.

16. МИНИМАЛЬНОЕ ПОКРЫТИЕ

УСЛОВИЕ. Задано семейство C подмножеств конечного множества S и положительное целое число K |C|.

ВОПРОС. Существует ли покрытие C' из C мощности не более K? Иными словами, существует ли в C такое подмножество C', что любой элемент из S принадлежит, по крайней мере, одному подмножеству из C'?

17. МИНИМАЛЬНЫЙ НАБОР ТЕСТОВ

УСЛОВИЕ. Задано конечное множество A возможных диагнозов, набор C подмножеств множества A, представляющий тесты, и положительное целое число J |C|.

ВОПРОС. Существует ли в C поднабор C' мощности не более J, такой, что для любой пары A_i, A_j возможных диагнозов имеется некоторый тест c Є C', содержащий ровно один из них?

18. САМЫЙ ДЛИННЫЙ ПУТЬ

УСЛОВИЕ. Заданы граф G=<V, E>, целые положительные длины l(e) для всех ребер, выделенные вершины s и t и положительное целое число B.

ВОПРОС. Существует ли в G элементарный путь из s в t, имеющий длину не менее B?

19. НЕЗАВИСИМОЕ МНОЖЕСТВО

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|.

ВОПРОС. Существует ли в V независимое множество мощности не менее K? Иными словами, верно ли, что существует подмножество V' Є V такое, что |V'| ³ K и никакие две вершины из V' не соединены ребром из E?

20. КУБИЧЕСКИЙ ПОДГРАФ

УСЛОВИЕ. Задан граф G=<V, E>.

ВОПРОС. Существует ли в E непустое подмножество E' такое, что в графе G'=<V, E'> любая вершина имеет степень, равную 3 или 0?

21. МИНИМАЛЬНЫЙ РАЗРЕЗ

УСЛОВИЕ. Заданы граф G=<V, E>, вес w(e) каждого ребра e Є E и положительное целое число K.

ВОПРОС.Существует ли разбиение множества V на два таких непересекающихся множества V₁ и V₂, что сумма весов ребер из E, соединяющих вершины из множеств V₁ и V₂, не превосходит K?

22. МИНИМАЛЬНЫЙ РАЗРЕЗ С ОГРАНИЧЕНИЯМИ

УСЛОВИЕ. Заданы граф G=<V, E> с двумя выделенными вершинами s и t, вес w(e) каждого ребра e Є E и положительные целые числа B и K (B |V|).

ВОПРОС. Существует ли разбиение множества V на два таких непересекающихся множества V₁ и V₂, что s Є V₁, t Є V₂, |V₁| B, |V₂| B и сумма весов ребер из E, соединяющих вершины из множеств V₁ и V₂, не превосходит K?

23. НАДЕЖНОСТЬ СЕТИ

УСЛОВИЕ. Заданы граф G=<V, E>, подмножество V' Є V, для каждого e Є E рациональное число p(e), 0 p(e) 1 – вероятность неисправности, положительное рациональное число q 1.

ВОПРОС. Верно ли, что с вероятностью, не меньшей q, любые две вершины из V соединены хотя бы одним путем, не содержащим неисправных ребер?

24. КРАТЧАЙШИЙ ПУТЬ С ОГРАНИЧЕНИЯМИ ПО ВЕСУ

УСЛОВИЕ. Заданы граф G=<V, E> с двумя выделенными вершинами s и t, целые положительные веса w(e) и длина l(e) каждого ребра e Є E и положительные целые числа B и K.

ВОПРОС. Существует ли в G элементарный путь из s в t, веса не более B и длины не более K?

25. СЕЛЬСКИЙ ПОЧТАЛЬОН

УСЛОВИЕ. Заданы граф G=<V, E>, целая положительная длина l(e) каждого ребра e Є E, E' – подмножество E и положительное целое число K.

ВОПРОС. Существует ли в G цикл, включающий каждое ребро из E' и имеющий длину не более K?

26. КИТАЙСКИЙ ПОЧТАЛЬОН

УСЛОВИЕ. Заданы смешанный граф граф G=<V, A, E>, где A – множество ориентированных ребер и E – множество неориентированных ребер; целая положительная длина l(e) каждого ребра 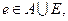и положительное целое число B.

ВОПРОС. Существует ли в G цикл, включающий по крайней мере один раз каждое ребро и имеющий длину не более B (ориентированные ребра должны входить в цикл только с правильной ориентацией)?

27. МИНИМАЛЬНОЕ ПО МОЩНОСТИ МАКСИМАЛЬНОЕ ПАРОСОЧЕТАНИЕ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |E|.

ВОПРОС. Существует ли в E непустое подмножество E' такое, что |E'| K и E'- максимальное паросочетание, т.е. никакие два ребра из E' не имеют общего конца, а любое ребро из множества E–E' имеет общий конец с одним из ребер множества E'?

28. СУММА ВЕСОВ

УСЛОВИЕ. Заданы конечное множество A, положительные целые веса w(a) для каждого a Є A и положительный целый вес K.

ВОПРОС. Существует ли такое подмножество A' множества A, что сумма весов его элементов равна K?

29. ДОМИНИРУЮЩЕЕ МНОЖЕСТВО

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|.

ВОПРОС. Существует ли в V доминирующее множество мощности не более K? Иными словами, верно ли, что существует подмножество V' Є V такое, что |V'| £ K и для любой вершины uÎV–V' сущеествует такая вершина vÎV’, что u и v соединены ребром из E?

30. РАЗБИЕНИЕ НА КЛИКИ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K≤ |V|.

ВОПРОС. Можно ли разбить вершины графа G на k ≤ K непересекающихся множеств V₁,V₂,…,V_k таких, что для всех i (1≤ i ≤ k) подграф, индуцированный множеством V_i, был бы полным?

31. РАЗБИЕНИЕ НА ТРЕУГОЛЬНИКИ

УСЛОВИЕ. Заданы граф G=<V, E> такой, что для некоторого положительного целого число q: |V|=3q.

ВОПРОС. Можно ли разбить вершины графа G на q непересекающихся множеств V₁,V₂,…,V_q таких, что каждое содержит ровно 3 вершины и для всех i (1≤ i ≤ q) подграф, индуцированный множеством V_i, был бы треугольником?

32. РАЗБИЕНИЕ НА ЛЕСА

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K ≤ |V|.

ВОПРОС. Можно ли разбить вершины графа G на k ≤ K непересекающихся множеств V₁,V₂,…,V_k таких, что для всех i (1≤ i ≤ k) подграф, индуцированный множеством V_i, не содержит циклов?

33. МОНОХРОМАТИЧЕСКИЙ ТРЕУГОЛЬНИК

УСЛОВИЕ. Заданы граф G=<V,E>.

ВОПРОС. Можно ли разбить множество ребер E на два непересекающихся подмножества E₁ и E₂, таких, что ни один из графов G₁=<V, E₁> или G₂=<V, E₂> не содержит треугольника?

34. ИНДУЦИРОВАННЫЙ ПУТЬ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|.

ВОПРОС. Существует ли в V подмножество V' такое, что |V'| ³ K и подграф, индуцированный множеством V', является элементарным путем на |V’| вершинах?

35. ДВУДОЛЬНЫЙ ПОДГРАФ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |E|.

ВОПРОС. Существует ли в E подмножество E’ мощности не менее K такое, что G’=<V, E’> – двудольный подграф?

36. СВЯЗНЫЙ ПОДГРАФ ОГРАНИЧЕННОЙ СТЕПЕНИ

УСЛОВИЕ. Заданы граф G=<V, E>, неотрицательное целое число d |V| и положительное целое число K |E|.

ВОПРОС. Существует ли в E подмножество E’ мощности не менее K такое, что подграф G’=<V, E’> связен и не имеет вершин степени более d?

37. ГАМИЛЬТОНОВО ПОПОЛНЕНИЕ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K |V|.

ВОПРОС. Существует ли множество E’, содержащее множество E такое, что |E’–E| £ K, а граф G’=<V, E’> имеет гамильтонов цикл?

38. КАРКАС ОГРАНИЧЕННОГО ДИАМЕТРА

УСЛОВИЕ. Заданы граф G=<V, E>, вес положительный целый вес w(e) каждого ребра e Є E и положительные целые числа B и D |V|.

ВОПРОС. Существует ли в графе G каркас T такой, что сумма весов ребер из T не превосходит B и в T нет элементарного пути, число ребер которого не превосходит D?

39. РАСЩЕПЛЕНИЕ МНОЖЕСТВА

УСЛОВИЕ. Задан набор C подмножеств множества S.

ВОПРОС. Существует ли такое разбиение множества S на два подмножества, что ни одно подмножество из C не содержится целиком ни в S₁, ни в S₂?

40. КРАТЧАЙШАЯ ОБЩАЯ НАДПОСЛЕДОВАТЕЛЬНОСТЬ

УСЛОВИЕ. Заданы конечный алфавит A, конечное множество R слов в алфавите A и положительное целое число K.

ВОПРОС. Существует ли такое слово w Є 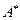, что |w| ≤ K и каждое слово x Є R есть подпоследовательность слова w (т.е. w = w₀x₁w₁x₂w₂…x_kw_k,, где w_i Є 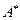, а x = x₁x₂…x_k)?

41. ПРЯМОУГОЛЬНОЕ СЖАТИЕ КАРТИНКИ

УСЛОВИЕ. Задана (0 – 1) матрица M порядка 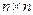и положительное целое число B.

ВОПРОС. Можно ли покрыть все единичные элементы матрицы M не более, чем B прямоугольниками? (Существует ли такая последовательность четверок (a_i, b_i, c_i, d_i,), 1 £ i £ B, где a_i £ b_i, c_i £ d_i, что для каждой пары индексов (i, j), 1 £ i, j £ n, 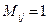тогда и только тогда, когда существует такое k, 1 £ k £ B, что a_i £ i £ b_i и c_i £ j £ d_i?

42. МАКСИМАЛЬНОЕ ЧИСЛО ОГРАНИЧЕННЫХ НЕПЕРЕСЕКАЮЩИХСЯ ПУТЕЙ

УСЛОВИЕ. Задан граф G=<V, E> с выделенными вершинами s и t и заданы положительные целые числа B и K (B и K ≤ |V|).

ВОПРОС. Верно ли что в G содержится не менее B путей из s в t, попарно не имеющих общих вершин и включающих не более K ребер?

43. КАРКАС ОГРАНИЧЕННОЙ СТЕПЕНИ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K ≤ |V|.

ВОПРОС. Существует ли в графе G каркас, у которого степени всех вершин не превосходят K?

44. КАРКАС С МАКСИМАЛЬНЫМ ЧИСЛОМ ЛИСТОВ

УСЛОВИЕ. Заданы граф G=<V, E> и положительное целое число K ≤ |V|.

ВОПРОС. Существует ли в графе G каркас, у которого не менее K вершин степени 1?

45. ДЕРЕВО ШТЕЙНЕРА

УСЛОВИЕ. Заданы граф G=<V, E> , положительный целый вес w(e) каждого ребра e Є E, подмножество R вершин графа и положительное целое число B.

ВОПРОС. Существует ли в графе G дерево, содержащее все вершины из R, что сумма весов ребер этого поддерева не превосходит B?

46. МАКСИМАЛЬНОЕ ЧИСЛО ОГРАНИЧЕННЫХ НЕПЕРЕСЕКАЮЩИХСЯ ПУТЕЙ

УСЛОВИЕ. Заданы граф G=<V, E> с выделенными вершинами s и t, а также положительные целые числа J и K.

ВОПРОС. Верно ли, что в G содержится не менее J различных путей из s в t, попарно не имеющих общих вершин и включающих не более K ребер?