Разработка программ, реализующих комбинацию численных методов

Вторая курсовая работа заключается в разработке программы, реализующей решение уравнения одним из перечисленных методов в случае, когда в уравнение входит интеграл от известной функции с неизвестным параметром, который должен быть определен при решении уравнения.

Рассмотрим задачу

.

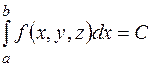При этом параметр z cчитается заданным, а y(z) определяется из решения уравнения. Таким образом, для решения задачи требуется использование одного из методов численного решения нелинейных уравнений и одного из методов численного интегрирования функций.

При разработке программ, реализующих численные методы, необходимо придерживаться общепринятого стиля: подпрограмма, реализующая конкретный метод, должна обладать определенной универсальностью и независимостью от вида функции, к которой применяется численный метод.

Из этого следует, что подпрограмма численного интегрирования в качестве формальных параметров должна содержать пределы интегрирования a,b верхнюю оценку погрешности e, имя подынтегральной функции, которая внутри подпрограммы должна иметь вид f(x). Поэтому параметры y и z не включаются в число формальных, а значит, являются внешними. Экстраполяция и оценка погрешности должна быть включена в подпрограмму численного интегрирования. Визуализация результатов экстраполяции должна быть предусмотрена и включаться в определенный момент расчета (как правило, в конце) по желанию пользователя.

Подпрограмма решения нелинейного уравнения 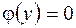в качестве формальных параметров должна содержать границы интервала поиска A,B, верхнюю границу погрешности решения уравнения E, имя функции 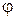, имя переменной y, значение которой является выходным параметром. В связи с этим, необходима подпрограмма, вычисляющая значения этой функции. В нашем случае 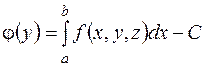. Параметры z и c являются для нее внешними. Из этой функции производится обращение к подпрограмме численного интегрирования. Примерная укрупненная блок-схема программы изображена на рис. 12.

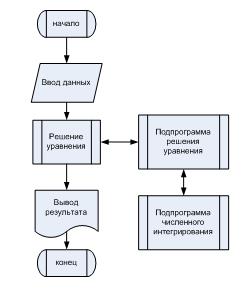
Рис. 12. Блок-схема программы, реализующей комбинацию численных методов

С помощью такой программы можно решить задачу построения зависимости y(z). Для этого необходимо задать последовательность значений z_j, j=1,…,M и вычислить соответствующие значения y_j=y(z_j). Результаты вычислений следует представить как в табличном, так и в графическом виде. Примерный графический интерфейс программы прилагается (прил. П3.1).

ПРИМЕР

Содержание курсовой работы рассмотрим на примере: “Оценка погрешности и уточнение методом Ромберга результатов численного дифференцирования по центрально-симметричной разностной формуле второго порядка”. В качестве дифференцируемой функции выберем 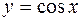при x=0.5.

1. Описание численного метода дифференцирования по центрально-симметричной разностной формуле второго порядка (см.п. 3).

2. Программная реализация метода дифференцирования по центрально-симметричной разностной формуле второго порядка (прилагается листинг программы с комментариями).

3. Оценка погрешности результата, уточнение результата, визуализация результатов уточнения.

3.1. В результате выполнения программы реализующей численное дифференцирование функции 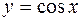, были получены следующие результаты z_n при следующих n (прил. П3.2)

При этом на каждом шаге происходит увеличение числа разбиений в 2 раза, т.е. Q=2.

3.2. Далее определяется разница результата на следующем и предыдущем шаге (прил. П3.3)

3.3. Вычисляем отношения (прил. П3.3.1)

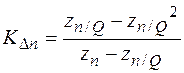
3.4. Потом экстраполируем полученный результат (прил. П3.3.2):

· Для метода Ромберга определяем порядок точности метода из приближенного равенства Q^k»K_Dn. Проводим экстраполяцию по формуле Ричардсона

;

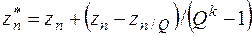· Для метода Эйткена для экстраполяции используется полученные значения K_Dn

.

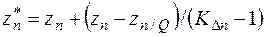Далее шаги 2,3 повторяются, до тех пор, пока 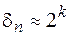. Нарушение этого равенства свидетельствует о том, что дальнейшее уточнение результата невозможно.

3.5. Строятся графики в логарифмической шкале:

a) Строится график полученных результатов в сравнении с точным результатом. По оси абсцисс откладывается lgn, по оси ординат значения , , ….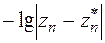

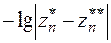Полученные результаты прилагаются (прил. П3.3.3).

b) Строится график полученных результатов в сравнение с “эталонным” значением. В качестве эталона выбирается наиболее точный результат z, полученный в результате последней экстраполяции. По оси абсцисс откладывается lgn, по оси ординат значения , , ,…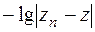

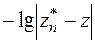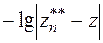Полученные результаты прилагаются (прил. П3.3.4).

c) Оценка результатов производится по правилу Рунге 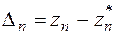, ,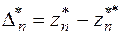… Строится график полученных результатов,

По оси абсцисс откладывается log₁₀n, по оси ординат значения -log₁₀ï 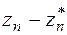ï, -log₁₀ú 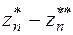ê, …

Полученные результаты прилагаются (прил. П3.3.5).

ВАРИАНТЫ ЗАДАНИЙ

1. Численное интегрирование методом левых прямоугольников.

2. Численное интегрирование методом правых прямоугольников.

3. Численное интегрирование методом трапеций.

4. Численное интегрирование методом средних прямоугольников.

5. Численное дифференцирование. Левая разностная формула первого порядка.

6. Численное дифференцирование. Правая разностная формула первого порядка.

7. Численное дифференцирование. Центрально-симметричная разностная формула второго порядка.

8. Численное дифференцирование. Вторая производная. Центрально-симметричная разностная формула второго порядка.

9. Численное решение задачи Коши методом Эйлера.

10. Численное решение задачи Коши усовершенствованным методом Эйлера.

11. Численное решение задачи Коши методом Рунге-Кутта 2-го порядка точности.

12. Краевая задача для обыкновенного линейного дифференциального уравнения. Метод конечных разностей.

13. Метод простых итераций для решения нелинейных уравнений.

14. Численное решение задачи Коши методом Рунге-Кутта 4-го порядка.

15. Численное решение задачи Коши методом Адамса 4-го порядка.

16. Численное решение смешанной задачи для уравнения теплопроводности методом конечных разностей по явной схеме.

17. Численное решение смешанной задачи для уравнения теплопроводности методом конечных разностей по неявной схеме

18. Численное решение смешанной задачи для волнового уравнения по явной трехслойной схеме.

19. Численное решение краевой задачи для уравнения Лапласа на прямоугольной области с применением метода Гаусса-Зейделя.

20. Интерполяция функции. Сравнение методов оценки погрешности (с помощью увеличения степени многочлена и уменьшения шага разбиения).

Методы экстраполяции

1. Метод Ромберга

2. Метод Нэвилла.

3. Метод Эйткена (d²-алгоритм).

4. e-алгоритм.

Приложение

П3.1. Графический интерфейс программы

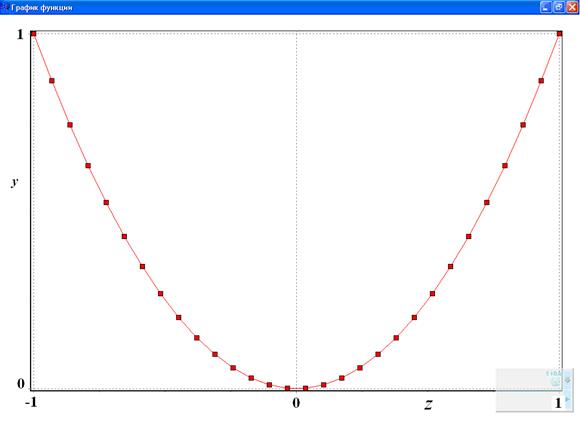
Рис. П3.1. График искомой функции y(z)

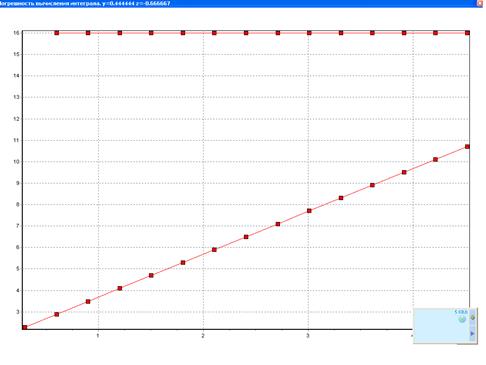
Рис. П.2. Оценка погрешности численных результатов

П.2.Численные результаты

ni	zn
	-.8068453602226698
	-.8594512716504229
	-.8730213311404762
	-.8764404712456473
	-.8772969276777106
	-.8775111463634158
	-.8775647075727431
	-.8775780982837214
	-.8775814459870084
	-.8775822829144317
	-.8775824921463595
	-.8775825444545262
	-.8775825575312410
	-.8775825608026935
	-.8775825616321526
	-.8775825618649833
	-.8775825621560216
	-.8775825621560220
	-.8775825649499893
	-.8775825649499880

П.3. Оценка и уточнение численных результатов

ni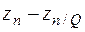
	-0.052605911
	-0.013570059
	-0.003419140
	-0.000856456
	-0.000214219
	-5.35612E-05
	-1.33907E-05
	-3.34770E-06
	-8.36927E-07
	-2.09232E-07
	-5.23082E-08
	-1.30767E-08
	-3.27145E-09
	-8.29459E-10
	-2.32831E-10
	-2.91038E-10
	-9.99201E-16
	-2.79397E-09
	9.99201E-16

П.3.1. Коэффициент уменьшения погрешности при удвоении n

ni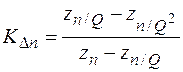
	3.87661612
	3.96885155
	3.99219386
	3.99804727
	3.99951174
	3.99987793
	3.99996948
	3.99999235
	3.99999862
	3.99998585
	4.00009994
	3.99722052
	3.94407947
	3.56249395
	0.80000175
	291270.889
	3.5763E-07
	-2796201.9

П.3.2. Вычисление экстраполированного значения

ni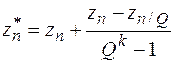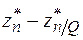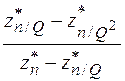
	-0.876986575
	-0.877544684	-0.000558109
	-0.877580185	-3.55003E-05	15.72124
	-0.877582413	-2.22854E-06	15.92984
	-0.877582553	-1.39437E-07	15.98243
	-0.877582561	-8.71720E-09	15.99560
	-0.877582562	-5.44861E-10	15.99894
	-0.877582562	-3.40566E-11	15.99868
	-0.877582562	-2.13496E-12	15.95190
	-0.877582562	-9.63674E-14	22.15438
	-0.877582562	-2.46692E-13	0.390639
	-0.877582562	4.35652E-13	-0.566260
	-0.877582562	-3.03102E-12	-0.143730
	-0.877582562	-1.54612E-11	0.196041
	-0.877582562	-3.39551E-11	0.455343
	-0.877582562	-3.10440E-10	0.109377
	-0.877582562	9.70114E-11	-3.200040
	-0.877582566	-3.72529E-09	-0.026040
	-0.877582565	9.31324E-10	-3.999990

П.3.3. Результат экстраполяции в сравнении с точным значением

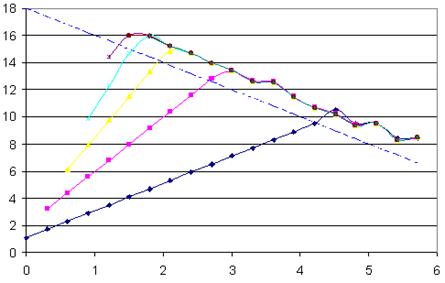
Рис. П.3. Результат экстраполяции в сравнении с точным значением

П.3.4. Результат экстраполяции в сравнении с “эталонным” значением

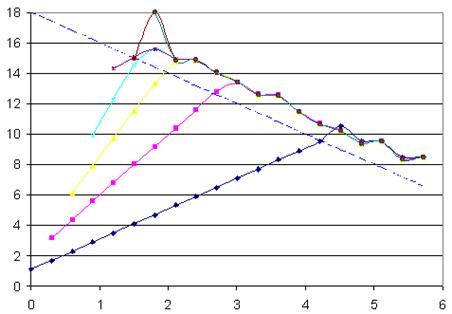
Рис. П.4. Результат экстраполяции в сравнении с “эталонным” значением

П3..5. Результат экстраполяции с оценкой погрешности по правилу Рунге (сравнением с «правым соседом»)

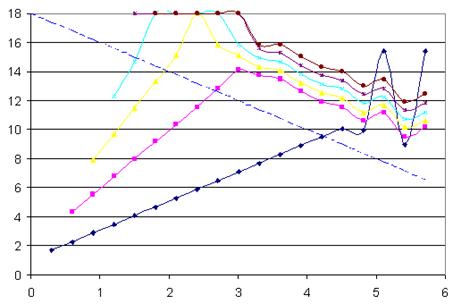
Рис. П.5. Результат экстраполяции с оценкой погрешности по правилу Рунге