ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ. Перед началом работы необходимо убедиться, что в ячейках нет шариков

Перед началом работы необходимо убедиться, что в ячейках нет шариков.

Часть 1

1. Постепенно выпустить из хранилища все шарики.

2. С помощью линейки измерить высоты получившихся столби-ков шариков в каждой ячейке – 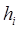и занести результаты, округлив их до 0,5 см, в таблицу 1.

3. Перевернув доску Гальтона, пересыпать все шарики в храни-лище, расположенное в верхней части доски.

Таблица 1

№ п/п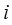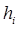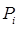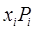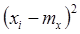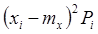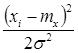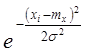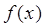
…

Часть 2

1. Выпустить из хранилища поочередно 3 шарика и записать в таблицу 3 значения координаты 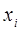, т.е. номера ячеек, куда попали шарики.

2. Аналогичные опыты проделать еще 4 раза и заполнить четыре таблицы, аналогичные таблице 2 (3,4,5,6).

Таблица 2

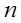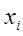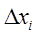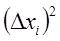				Доверительный интервал
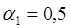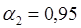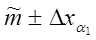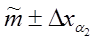Среднее

Обработка реЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Часть 1

1. Подсчитать сумму высот 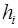во всех ячейках .

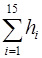2. По формуле (3.3.12) определить экспериментальное значение вероятности попадания шарика в каждую ячейку 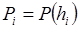. Резуль-таты занести в таблицу 1.

3. Вычислить произведение 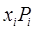и тоже занести в соответствую-щие столбцы таблицы 1. Подсчитать математическое ожидание оп-ределяемой координаты выпускного отверстия по формуле (1.11), взяв 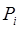, полученное в предыдущем пункте.

4. Вычислить величину 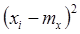и занести в таблицу 1.

5. Вычислить и занести в таблицу 2 значения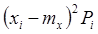

6. По формуле (1.23) определить среднее квадратичное откло-нение .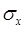

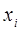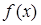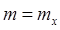7. Для каждого подсчитать по формуле (1.26) значение функ-ции , где и .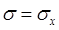

8. В одних осях координат построить график вероятности 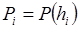в зависимости от координаты 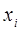и график функции 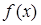. Сравнить полученные кривые.

Часть 2

1. Найти оценку математического ожидания 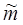координаты вы-пускного отверстия по формуле (3.3.3) для каждой из пяти серий измерений.

2. Найти погрешность :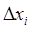

,

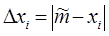а также 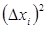для каждого измерения и занести результаты в таблицы 2-6.

3. По формуле (3.3.7), заменив предварительно величину 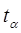на коэффициент Стьюдента 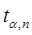, и с использованием формулы (3.3.8) вычислить 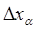отдельно для 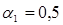и 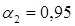, т.е. использовать формулу:

.

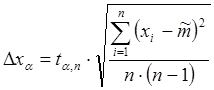4. Записать в каждой таблице, соответственно, для двух надеж-ностей ответы в виде:

.

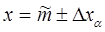5. В виде вывода по пяти сериям экспериментов записать отдельно для двух надежностей 0,5 и 0,95 количество случаев, в которых доверительный интервал перекрывает истинное значение координаты выпускного отверстия .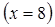

Контрольные вопросы

1. Какой процесс называется случайным?

2. Что такое случайная величина?

3. Какая величина называется частотой события?

4. Что называется законом распределения случайной величины?

5. Что такое функция распределения случайной величины?

6. Запишите основные свойства функции распределения случай-ной величины.

7. Укажите основные числовые параметры, характеризующие закон распределения случайной величины и объясните их смысл.

8. Что называется математическим ожиданием случайной вели-чины?

9. Дайте определение величины дисперсии.

10. Что называется средним квадратичным отклонением?

11. В чем удобство использования среднего квадратичного от-клонения по сравнению с использованием дисперсии?

12. Какова связь между функцией распределения и плотностью распределения?

13. Для каких случайных величин существует плотность распре-деления– дискретных или непрерывных?

14. Запишите основные свойства плотности распределения.

15. Что такое кривая распределения?

16. Запишите выражение для функции плотности распределения непрерывной случайной величины.

17. Какова вероятность принятия случайной величиной конкрет-ного значения при дискретном распределении? При непрерывном распределении?

18. Как влияет дисперсия случайной величины на форму кривой распределения?

19. Укажите аналог кривой распределения для дискретных слу-чайных величин.

20. Укажите оценку основных параметров распределения.

21. Какая оценка называется точечной?

22. Какая оценка называется несмещённой?

23. Что такое доверительная вероятность или надежность изме-рения?

24. Как измеряется доверительный интервал для среднего значе-ния измеряемой величины и что он обозначает?

25. В классической физике имеет место классическое распреде-ление Максвелла. Что это за распределение и чем оно отличается от нормального распределения?

26. Рассмотрев систему материальных точек с массами 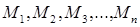, располагающимися на оси 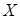в точках 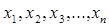, укажите механическую интерпретацию математического ожидания.

27. Воспользовавшись условиями предыдущего вопроса, укажи-те механическую интерпретацию дисперсии.

28. Как составляется статистический ряд?

29. Как производится построение гистограммы?

30. Как по гистограмме получить характеристики распределения случайной величины?