Показательный закон распределения. Привести пример
Показательное (экспоненециальное) распределение.Непрерывная случайная величина x, принимающая неотрицательные значения, имеет показательное распределение с параметром l>0, если плотность распределения вероятностей случайной величины равна
рx(x)= 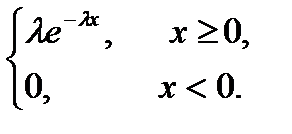
Функция распределения показательного распределения имеет вид
Fx(x)= 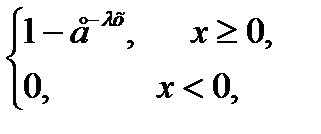
а математическое ожидание и дисперсия равныМx= 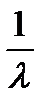 , Dx=
, Dx= 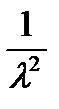 .
.
26. Нормальный закон распределения и его особенности. Привести пример.
Нормальное распределение (распределение Гаусса). Непрерывная случайная величина называется распределенной по нормальному закону с параметрами 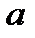 и
и 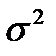 , если ее плотность распределения равна
, если ее плотность распределения равна
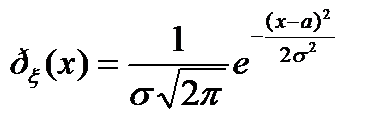 .
.
Через 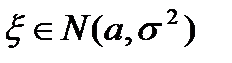 обозначается множество всех случайных величин, распределенных по нормальному закону с параметрами параметрами
обозначается множество всех случайных величин, распределенных по нормальному закону с параметрами параметрами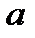 и
и 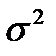 .
.
Функция распределения нормально распределенной случайной величины равна
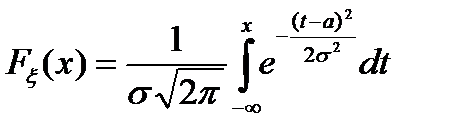 .
.
Параметры нормального распределения суть математическое ожидание 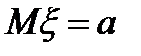 и дисперсия
и дисперсия 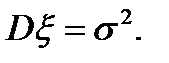
В частном случае, когда 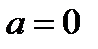 и
и 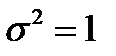 нормальное распределение называется стандартным, и класс таких распределений обозначается
нормальное распределение называется стандартным, и класс таких распределений обозначается 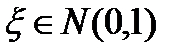 .
.
В этом случае плотность стандартного распределения равна
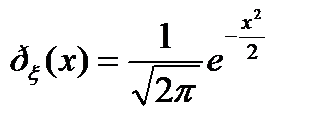 ,а функция распределения
,а функция распределения 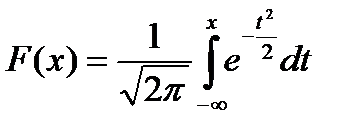
Поэтому вероятность попадания нормально распределенной случайной величины 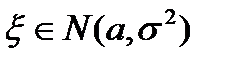 на интервал
на интервал 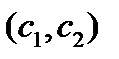 можно вычислять по формуле
можно вычислять по формуле
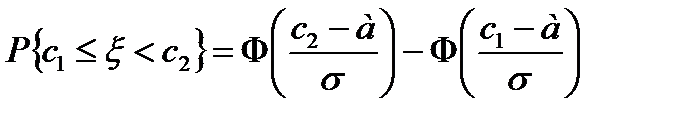 .
.
Неотрицательная случайная величина x называется логарифмически нормально распределенной, если ее логарифм h=lnxподчинен нормальному закону. Математическое ожидание и дисперсия логарифмически нормально распределенной случайной величины равны Мx= 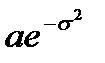 и
и
Dx= 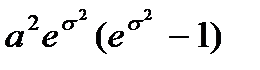 .
.
Система двух дискретных СВ. Функция распределения и её свойства.
Будем обозначать через (X, Y) двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой); обе величины X и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Функцией распределения двумерной случайной величины (X, Y) называют функцию F(x, y), определяющую для каждой пары чисел x, y вероятность того, что X примет значение, меньшее x, и при этом Y примет значение, меньшее y: F(x, y) = P(X<x, Y<y).
Свойство 1. Значения функции распределения удовлетворяют двойному неравенству 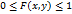 .
.
Свойство 2.F(x, y) есть неубывающая функция по каждому аргументу, т.е.
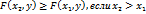 ;
; 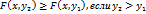
Свойство 3. Имеют место предельные соотношения:
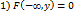 ; 2)
; 2) 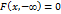 ; 3)
; 3) 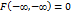 ; 4)
; 4) 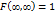
Свойство 4. а) При 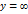 функция распределения системы становится функцией распределения составляющей Х:
функция распределения системы становится функцией распределения составляющей Х: 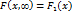 .
.
б) При 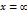 функция распределения системы становится функцией распределения составляющей Х:
функция распределения системы становится функцией распределения составляющей Х: 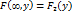 .
.
