Доверительные интервалы

Доверительный интервал для оценки неизвестного математического ожидания нормальной случайной величины..... 8

6 Доверительный интервал для неизвестной дисперсии нормальной случайной величины.........................................................9

7 Критерий согласия.....................................................................10

Исходные данные:

Построение интервального вариационного ряда

Элементы выборки, расположенные в порядке возрастания, образуют так называемый вариационный ряд. Пусть l - число различных выборочных

значений в данной выборке. Таблица 1 также называют вариационным

рядом:

Таблица 1. Вариационный ряд.

X	Частоты	Кол.	X	Частоты	Кол.	X	Частоты	Кол.	X	Частоты	Кол.

В таблице 2 приведены основные данные по вариационному ряду:

Таблица2. Основные данные по вариационному ряду.

X max
X min
Объём выборки (n)

Для определения оптимальной длины интервала можно использовать формулу Стерджеса:

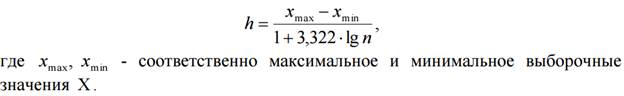
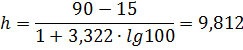
так как число h дробное, принимаем ближайшее целое – 10, то есть длина интервала – 10.

За начало первого интервала принимают величину

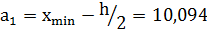
округлим до 10, таким образом, построим интервальный вариационный ряд:

Таблица 3. Интервальный вариационный ряд.

	X	N (частоты)	Относительная частота
1 интревал	10-20		0,05
2 интревал	20-30		0,1
3 интревал	30-40		0,17
4 интревал	40-50		0,2
5 интревал	50-60		0,19
6 интревал	60-70		0,15
7 интревал	70-80		0,12
8 интревал	80-90		0,02

Затем интервальный вариационный ряд условно заменяют дискретным, в

первой строке которого записывают средние значения интервалов (табл. 4):

Таблица 4. Дискретный ряд.

X среднее
Относительная частота	0,05	0,1	0,17	0,2	0,19	0,15	0,12	0,02

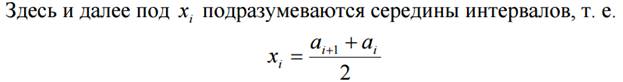
Гистограмма и полигон

Гистограмма – это ступенчатая фигура, состоящая из прямоугольников,

основания которых – интервалы длины h, а высоты - Wi/ h, т. е. площадь

каждого прямоугольника равна соответствующей относительной частоте.

Таблица 5. Данные для построения гистограммы и полигона.

	1 интревал	2 интревал	3 интревал	4 интревал	5 интревал	6 интревал	7 интревал	8 интревал
		20-30	30-40	40-50	50-60	60-70	70-80	80-90
X средн
h	9,811616954
W/h	0,005096	0,010	0,017	0,0203	0,01936	0,01528	0,0122	0,002038

.

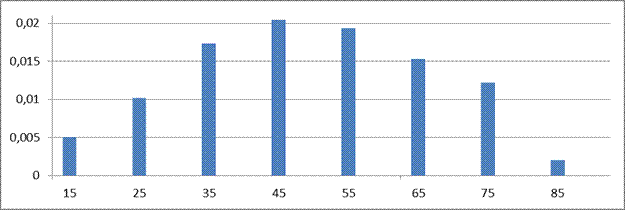
Рисунок 1 – Гистограмма.

Полигоном относительных частот называют ломаную, отрезки которой

соединяют точки (Wi, x), где x - середины интервалов, Wi- соответствующие им относительные частоты. Обычно по виду полигона выдвигают гипотезу о законе распределения дискретной случайной величины.

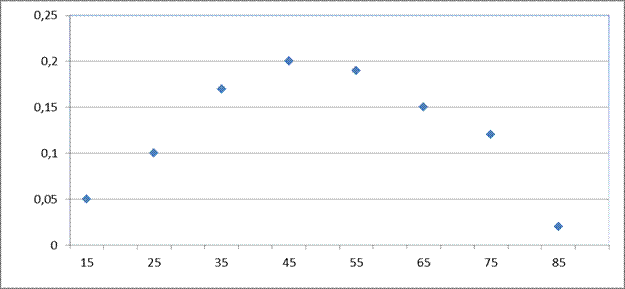
Рисунок 2 – Полигон.

Точечные оценки параметров

Предположим, что по виду гистограммы или полигона выдвинута гипотеза о виде закона распределения случайной величины. Возникает необходимость

определить неизвестные параметры этого закона распределения.

Таблица 6. Оценка выборочного среднего и выборочной дисперсии.

X среднее	n	X·n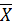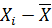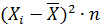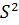
			49,1	-34,1	5814,05	304,19
			-24,1	5808,1
			-14,1	3379,77
			-4,1	336,2
			5,9	661,39
			15,9	3792,15
			25,9	8049,72
			35,9	2577,62
Сумма
				7,2

Доверительные интервалы

Точечная оценка может значительно отличаться от оцениваемого параметра. Чтобы дать представление о точности и надежности точечной оценки, строят доверительные интервалы.