Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
Колеблющееся тело может участвовать в нескольких колебательных процессах, тогда необходимо найти результирующее колебание, иными словами, колебания необходимо сложить. Сложим гармонические колебания одного направления и одинаковой частоты
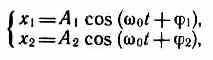
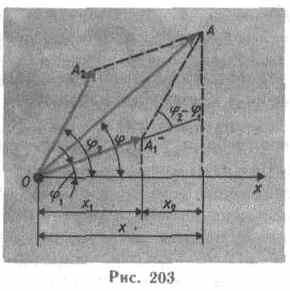
воспользовавшись методом вращающегося вектора амплитуды (см. § 140). Построим векторные диаграммы этих колебаний (рис.203). Так как векторы A1 и А2 вращаются с одинаковой угловой скоростью w0, то разность фаз (j2-j1) между ними остается постоянной.
Очевидно, что уравнение результирую-
щего колебания будет
х=х1+х2=Аcos(w0t+j). (144.1)
В выражении (144.1) амплитуда А и начальная фаза j соответственно задаются соотношениями
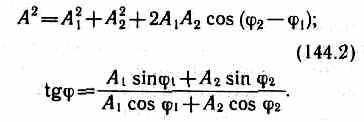
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (j2-j1) складываемых колебаний.
Проанализируем выражение (144.2) в зависимости от разности фаз (j2-j1):
1) j2-j1=±2mp (m = 0, 1, 2,...), тогда A=A1+A2, т.е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;
2) j2-j1= ±(2m+1)p (m=0, 1, 2,...), тогда A = │A1-A2│, т.е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний.
Для практики особый интерес представляет случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны w и w+Dw, причем Dw<<w. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:
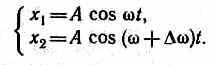
Складывая эти выражения и учитывая, что во втором сомножителе Dw/2<<w, найдем

Получившееся выражение есть произведение двух колебаний. Так как Dw<<w, то сомножитель, стоящий в скобках, почти не изменяется, когда сомножитель coswt совершит несколько полных колебаний. Поэтому результирующее колебание х можно рассматривать как гармоническое
с частотой w, амплитуда Аб, которого изменяется по следующему периодическому закону:
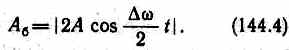
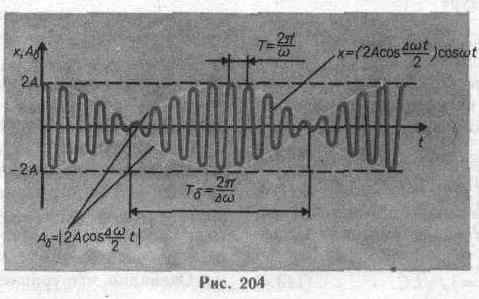
Частота изменения Aб, в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний: wб=Dw. Период биений
Tб=2p/Dw.
Характер зависимости (144.3) показан на рис. 204, где сплошные жирные линии дают график результирующего колебания (144.3), а огибающие их — график медленно меняющейся по уравнению (144.4) амплитуды.
Определение частоты тона (звука определенной высоты (см. §158)) биений между эталонным и измеряемым колебаниями — наиболее широко применяемый на практике метод сравнения измеряемой величины с эталонной. Метод биений используется для настройки музыкальных инструментов, анализа слуха и т. д.
Любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, кратными циклической частоте w0:
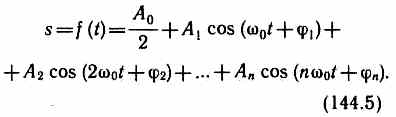
Представление периодической функции в виде (144.5) связывают с понятием гармонического анализа сложного периодического колебания,или разложения Фурье.
Члены ряда Фурье, определяющие гармонические колебания с частотами w0, 2w0, 3w0,..., называются первой(или основной),
второй, третьей и т. д. гармоникамисложного периодического колебания.
