Формальные языки и грамматики: Формы описания синтаксиса (символьная, БНФ, итерационная, синтаксические диаграммы)
Формальные языки и грамматики: задачи распознавания и синтаксического анализа.
Процесс построения цепочки с помощью правил заданной грамматики называется задачей порождения цепочки. Если задана цепочка терминальных символов и требуется определить принадлежит ли эта цепочка языку, порождаемому грамматикой, то это задача распознавания. Если в процессе распознавания необходимо определить с помощью каких правил грамматики может быть построена заданная цепочка (синтаксический разбор), такая задача называется синтаксическим анализом. В общем виде задачу распознавания можно определить с помощью операции сворачивания, которая является противоположностью вывода.
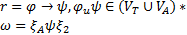
Где 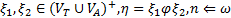 .
.
Если задана последовательность цепочек 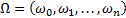 .
. 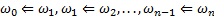 .
.
Если задана цепочка 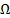 с помощью правил заданной грамматики может быть свернута, то она принадлежит языку, порождаемому данной грамматикой.
с помощью правил заданной грамматики может быть свернута, то она принадлежит языку, порождаемому данной грамматикой.
Формальные языки и грамматики: Формы описания синтаксиса (символьная, БНФ, итерационная, синтаксические диаграммы).
1) Символьное обозначение - в виде порождающих правил;
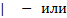
D – цифра, N – число.
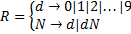
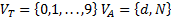
2) Нормальная форма Бекуса (БНФ);
Вместо терминального символа используются слова или группы слов, которые называются металингвистическими переменными и заключаются в угловые скобки. Вместо 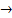 используется символ
используется символ 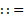 (это есть).
(это есть).
Определим синтаксис числа с помощью БНФ.
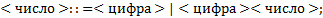
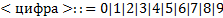
3) Итерационная ( 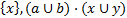 );
);
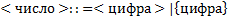
4) Синтаксические диаграммы;
Определяемое понятие всегда пишется слева от диаграммы без рамки. Каждому нетерминальному символу соответствует прямоугольник, внутри которого записывается символ, каждому терминальному символу соответствует кружок, порядок следования определяется стрелками. Синтаксические диаграммы определяются для каждого правила.
4. Формальные языки и грамматики: классификация грамматик по типам. Существует 4 основных типов грамматик (Хомский). Тип 0; Сюда относятся грамматики, не имеющих ограничение на вид правил: 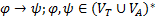 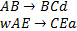 Тип 1 – контекстно-зависимая или грамматики с непосредственной составляющей; Для данного типа грамматики правила имеют вид: Тип 1 – контекстно-зависимая или грамматики с непосредственной составляющей; Для данного типа грамматики правила имеют вид: 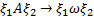 , где , где 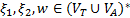 . . 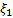 - левый контекст, а - левый контекст, а 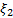 - правый контекст. Например: - правый контекст. Например: 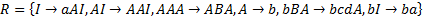 . Такой тип можно использовать на практике. Тип 2 – контекстно-свободная грамматика; . Такой тип можно использовать на практике. Тип 2 – контекстно-свободная грамматика; 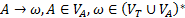 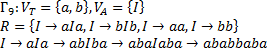 Грамматика Грамматика 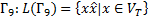 . Автоматной грамматикой или регулярной грамматикой; . Автоматной грамматикой или регулярной грамматикой; 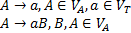 Бывает правосторонняя (все правила вправо) или левосторонняя (все правила влево). 5. Автоматные грамматики: определение А-грамматик и конечного автомата. Конечный автомат задается следующей совокупностью множеств Бывает правосторонняя (все правила вправо) или левосторонняя (все правила влево). 5. Автоматные грамматики: определение А-грамматик и конечного автомата. Конечный автомат задается следующей совокупностью множеств 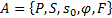 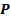 - входной алфавит. - входной алфавит. 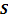 - алфавит состояний. - алфавит состояний. 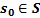 - начальный символ. - начальный символ. 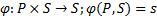 Входная лента разделена на позиции, где может быть расположен один символ, выходом автомата являются сигналы состояния. Автомат работает по тактам, в каждом такте осуществляется чтение входного символа, определение нового входного символа и сдвиг входной считывающей головки на одну позицию вправо. Чтобы описать работу автомата введем понятие конфигурация. Конфигурация состоит из состояния Входная лента разделена на позиции, где может быть расположен один символ, выходом автомата являются сигналы состояния. Автомат работает по тактам, в каждом такте осуществляется чтение входного символа, определение нового входного символа и сдвиг входной считывающей головки на одну позицию вправо. Чтобы описать работу автомата введем понятие конфигурация. Конфигурация состоит из состояния 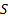 и части цепочки и части цепочки 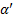 , которая не прочитана на входной ленте. Выделим начальную конфигурацию из цепочки полностью записанной на входной ленте. Каждый такт работы связан с определенной конфигурацией. Работу автомата можно представить как последовательную смену конфигураций. Рассмотрим один такт работы. , которая не прочитана на входной ленте. Выделим начальную конфигурацию из цепочки полностью записанной на входной ленте. Каждый такт работы связан с определенной конфигурацией. Работу автомата можно представить как последовательную смену конфигураций. Рассмотрим один такт работы. 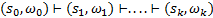 Входная цепочка Входная цепочка 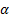 называется допустимой для конечного автомата, если при последовательном чтении символов этой цепочки: называется допустимой для конечного автомата, если при последовательном чтении символов этой цепочки: 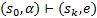 , множество цепочек допускаемых автоматом называется языком, допускаемым этим автоматом. , множество цепочек допускаемых автоматом называется языком, допускаемым этим автоматом. 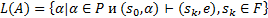 . Пусть на входе автомата записана некоторая цепочка, конечный автомат представляется собой устройство решающее задачу распознавания, если последовательно считывая символы цепочки, автомат приходит в заключительную конфигурацию, то цепочка допустима, т.е. принадлежит автомату и наоборот. Правила построения конечного автомата по заданной грамматике: 1) Преобразование грамматики; Пусть дана правосторонняя автоматная грамматика. a. Введем вспомогательный символ . Пусть на входе автомата записана некоторая цепочка, конечный автомат представляется собой устройство решающее задачу распознавания, если последовательно считывая символы цепочки, автомат приходит в заключительную конфигурацию, то цепочка допустима, т.е. принадлежит автомату и наоборот. Правила построения конечного автомата по заданной грамматике: 1) Преобразование грамматики; Пусть дана правосторонняя автоматная грамматика. a. Введем вспомогательный символ 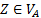 ; b. все заключительные правила преобразуем к виду ; b. все заключительные правила преобразуем к виду 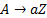 ; c. ; c. 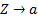 . . 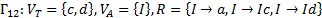 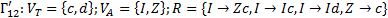 2) Построение автомата; Для каждого КА существует автоматная грамматика, порождающая язык, которая совпадает с языком допускаемым заданным автоматом. 6. Автоматные грамматики: недетерминированный конечный автомат (НКА). Если в некотором состоянии S в автомате определены несколько переходов под действием одного и того же символа 2) Построение автомата; Для каждого КА существует автоматная грамматика, порождающая язык, которая совпадает с языком допускаемым заданным автоматом. 6. Автоматные грамматики: недетерминированный конечный автомат (НКА). Если в некотором состоянии S в автомате определены несколько переходов под действием одного и того же символа 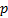 , то такой автомат недетерминированный. Недетерминированный конечный автомат задается следующей совокупностью множеств: , то такой автомат недетерминированный. Недетерминированный конечный автомат задается следующей совокупностью множеств: 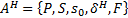 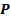 - входной алфавит. - входной алфавит. 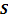 - алфавит состояний. - алфавит состояний. 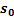 -начальное состояние. -начальное состояние. 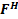 - множество заключительных состояний. - множество заключительных состояний. 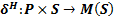 - функция переходов. Если для заданного входного слова, подаваемого на вход недетерминированного конечного автомата, существует последовательность состояний в которой первое состояние является начальным, а последнее заключительным (одно из заключительных), то это слово – допустимое входное слово. Множество допустимых входных слов называется языком совместимым с заданным НКА. дано НКА: - функция переходов. Если для заданного входного слова, подаваемого на вход недетерминированного конечного автомата, существует последовательность состояний в которой первое состояние является начальным, а последнее заключительным (одно из заключительных), то это слово – допустимое входное слово. Множество допустимых входных слов называется языком совместимым с заданным НКА. дано НКА: 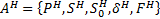 , построить ДКА , построить ДКА 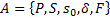 . 1) Пусть . 1) Пусть 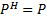 ; 2) Распишем множество всевозможных состояния для какого-то состояния ; 2) Распишем множество всевозможных состояния для какого-то состояния 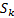 , оно будет выглядеть как: , оно будет выглядеть как: 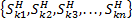 , каждому такому подмножеству множество состояний НКА поставим в соответствие одно состояние искомого , каждому такому подмножеству множество состояний НКА поставим в соответствие одно состояние искомого 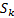 . 3) Определим множество заключительных состояний искомого ДКА: . 3) Определим множество заключительных состояний искомого ДКА: 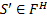 и и 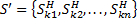 , то , то 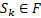 . 4) . 4) 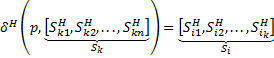 , , 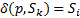 |
