Б) Теорема в интегральной (конечной) форме

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов всех внешних сил, действующих на точки механической системы, за тот же промежуток времени.

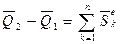
Следствия из теоремы:

1. Если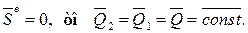

2. Если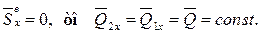

12. Кинетическим моментомилиглавныммоментом количеств движения

Механической системы относительно некоторого центра (оси) называется геометрическая (алгебраическая) сумма моментов количеств движения всех материальных точек системы, относительно того же центра. (оси).

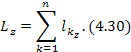
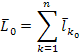
.Кинетический момент твердого тела, вращающегося во­круг неподвижной оси z с угловой скоростью 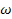равен

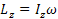
Теорема об изменении кинетического момента механической системы относительно центра и оси

а) Теорема моментов относительно центра.

Производная по времени от кинетического момента ме­ханической системы относительно некоторого неподвижно­го центра равна геометрической сумме моментов всех внеш­них сил, действующих на систему, относительно того же центра.

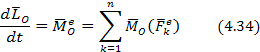
Следствие. Если главный момент внешних сил относи­тельно некоторого центра равен нулю, то кинетический мо­мент системы относительно этого центра не изменяется (за­кон сохранения кинетического момента).

Б) Теорема моментов относительно оси.

Производная по времени от кинетического момента ме­ханической системы относительно некоторой неподвижной оси равна сумме моментов всех внешних сил, действующих на систему, относительно этой оси.

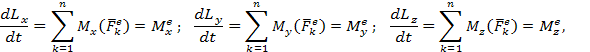
Следствие.Если главный момент внешних сил относи­тельно некоторой оси равен нулю, то кинетический момент системы относительно этой оси не изменяется.

14. Работа силы — скалярная мера действия силы.

Элементарная работа силы — это бесконечно малая ска­лярная величина, равная скалярному произведению вектора силы на вектор бесконечного малого перемещения точки приложения силы.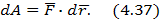

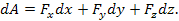
15. Кинетическая энергия материальной точки — скалярная положительная величина, равная половине произведения массы точки на квадрат ее скорости, т. е. .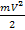

Теорема Кенига

Кинетическая энергия механической системы в общем случае ее движения равна сумме кинетической энергии движения системы вместе с центром масс и кинетической энергии системы при ее движении относительно центра масс:

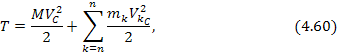
1. Работа силы тяжести.	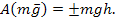4. Поступательное движение.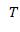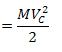
2.Работа силы упругости пружины.	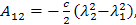5. Вращение тела вокруг неподвижной оси .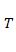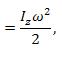
3.Работа момента	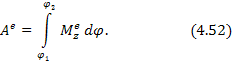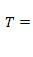6. Плоскопараллельное движение.

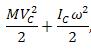17.Теорема об изменении кинетической энергии материальной точки