Случайные величины. Многоугольник распределения

Рассмотренный выше пример позволяет сделать вывод, что значения, используемые для анализа зависят от случайных причин, поэтому такие переменные величины называются случайными. В большинстве случаев они появляются в результате наблюдений или экспериментов, которые сводятся в таблицы, в первой строке которой записываются различные наблюдаемые значения случайной величины Х, а во второй – соответствующие частоты. Поэтому такая таблица называется эмпирическим распределением случайной величины Х или вариационным рядом. Для вариационного ряда мы находили среднее значение 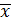, дисперсию 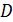и среднее квадратическое отклонение .

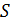Случайная величина называется непрерывной, если ее значения целиком заполняют некоторый числовой промежуток.

Случайная величина называется дискретной, если все ее значения можно занумеровать (в частности, если оно принимает конечное число значений).

Следует отметить два характерных свойства таблицы распределения дискретной случайной величины:

- все числа второй строки таблицы положительны;

- их сумма равна единице.

В соответствие с проведенными исследованиями можно предположить, что при увеличении числа наблюдений эмпирическое распределение приближается к теоретическому, заданному в табличной форме.

Важной характеристикой дискретной случайное величины является ее математическое ожидание.

Математическим ожиданием дискретной случайной величины Х, принимающей значения 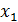, , 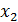…, 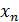.с вероятностями 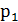, , 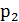…, 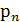называется число:

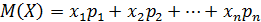. (7)

Математическое ожидание также называют средним значением.

К другим важным характеристикам случайной величины относятся дисперсия (8) и среднее квадратическое отклонение (9).

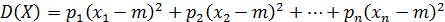, (8)

где: 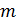математическое ожидание величины X.

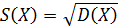. (9)

Графическое представление информации значительно нагляднее, чем табличное, поэтому возможность электронных таблиц MS Excel представлять размещенные в них данные в виде различных диаграмм, графиков и гистограмм используется очень часто. Так, помимо таблицы, распределение случайной величины изображают также с помощью многоугольника распределения. Для этого на координатной плоскости строят точки с координатами 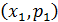, , 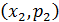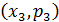… и соединяют их прямыми отрезками.

Для получения прямоугольника распределения посредством MS Excel необходимо:

1. Выбрать на панели инструментов закладу «Вставка» ® «Диаграмма с областями».

2. Активизировать появившуюся на листе MS Excel область для диаграммы правой кнопкой мыши и в контекстном меню воспользоваться командой «Выбрать данные».

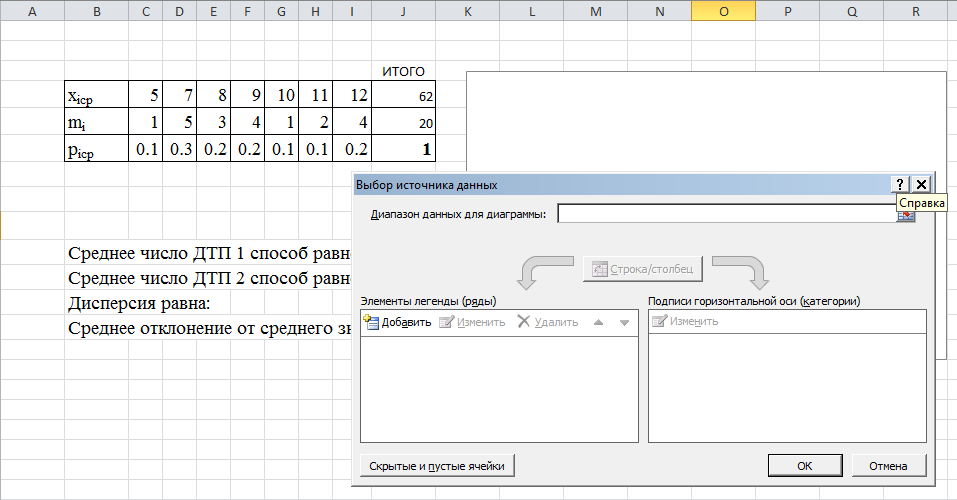
Рис. 6. Выбор источника данных

Сначала определим диапазон данных для диаграммы. Для этого в соответствующую область диалогового окна «Выбор источника данных» введем диапазон C6:I6 (в нем представлены значения частот 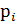под названием Ряд1, рис. 7).

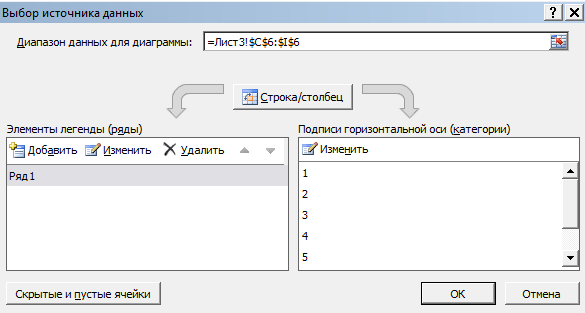
Рис. 7. Добавление ряда 1

Для изменения названия ряда необходимо выбрать кнопку изменить область «Элементы легенды (ряды)» (см. рис. 7) и назвать его .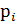

Для того, чтобы добавить подпись оси X необходимо воспользоваться кнопкой «Изменить» области «Подписи горизонтальной оси (категории)»
(рис. 8) и указать значения ряда 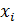(диапазон $C$6:$I$6).

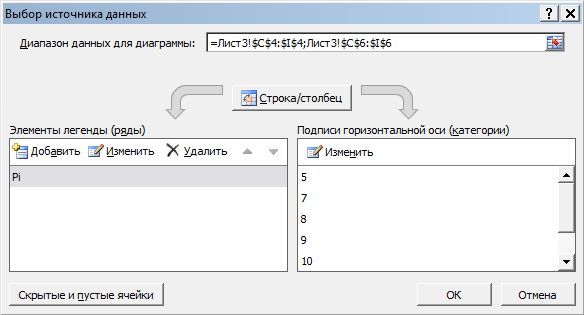
Рис. 8. Окончательный вид окна диалога «Выбор источника данных»

Выбор кнопки в окне диалога «Выбор источника данных»
(рис. 8) позволит получить требуемый многоугольник распределения случайной величины (рис. 9).

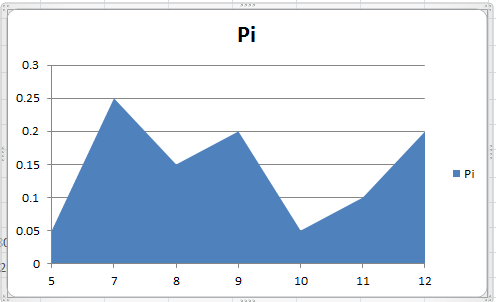
Рис. 9. Многоугольник распределения случайной величины

Внесем некоторые изменения в дизайн полученной графической информации:

- добавим подпись оси Х;

- отредактируем подпись оси Y;

- добавим заголовок для диаграммы «Многоугольник распределения».

Для этого выберем в области панели инструментов закладку «Работа с диаграммами» закладку «Макет» и в появившейся панели инструментов соответствующие кнопки: «Название диаграммы», «Названия осей» (рис. 10).

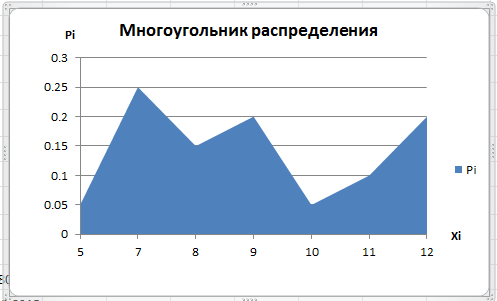
Рис. 10. Итоговый вид многоугольника распределения случайной величины