Указания по выполнению практических заданий
Прежде чем приступит к выполнению практических заданий, рекомендуется ознакомиться с соответствующей темой из теоретического раздела и разобранными примерами решения типовых задач.
Требования к математической подготовке читателя ограничиваются обычными курсами математического анализа и теории вероятностей.
Тема 1. Введение. Основы теории вероятностей и финансовой математики
Задача 1.1.Контрольная работа по теории вероятностей состоит из трех заданий. Первое задание оценивается на 6 баллов, второе на 10 баллов и последнее – 4 балла. Вероятность того, что студент специальности ПИвЭ решит правильно первое задание, равна  ; второе –
; второе –  ; третье –
; третье –  . Какова вероятность того, что средний балл за контрольную работу в потоке из 60 человек будет меньше 13?
. Какова вероятность того, что средний балл за контрольную работу в потоке из 60 человек будет меньше 13?
Решение.
Случайная величина 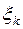
 – количество баллов, полученных за контрольную работу студентом специальности ПИвЭ.
– количество баллов, полученных за контрольную работу студентом специальности ПИвЭ.  – последовательность независимых, одинаково распределенных случайных величин. Составим ряд распределения этой случайной величины и найдем ее числовые характеристики – математическое ожидание
– последовательность независимых, одинаково распределенных случайных величин. Составим ряд распределения этой случайной величины и найдем ее числовые характеристики – математическое ожидание  и среднее квадратическое отклонение
и среднее квадратическое отклонение  .
.
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.
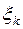 | |||||||
 | 0,02 | 0,18 | 0,03 | 0,29 | 0,18 | 0,03 | 0,27 |
 ;
;
 .
.
Используя центральную предельную теорему, найдем вероятность того, что средний балл за контрольную работу в потоке будет меньше 13.

Задача 1.2.Вероятность попадания в цель при одном выстреле равна 0,002. Цель уничтожается при условии двух и более попаданий. Найти вероятность уничтожения цели, если произведено 1000 независимых выстрелов.
Решение.
Поскольку число испытаний (количество независимых выстрелов)  достаточно велико, вероятность успеха (попадание в цель)
достаточно велико, вероятность успеха (попадание в цель)  достаточно мала (
достаточно мала (  ), то для вычисления вероятности хотя бы двух попаданий в цель воспользуемся приближенной формулой Пуассона:
), то для вычисления вероятности хотя бы двух попаданий в цель воспользуемся приближенной формулой Пуассона:
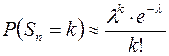 .
.
Тогда имеем

Задача 1. 3.Среди клиентов банка 80% являются физическими лицами и 20% – юридическими. Из практики известно, что 40% всех операций приходится на долгосрочные расчеты, в то же время из общего числа операций, связанных с физическими лицами, 30% приходится на долгосрочные расчеты. Какова вероятность того, что наудачу выбранный клиент является юридическим лицом и осуществляет долгосрочный расчет?
Решение.
Рассмотрим следующие события  {клиент является физическим лицом},
{клиент является физическим лицом},  {клиент осуществляет долгосрочный расчет}. Тогда
{клиент осуществляет долгосрочный расчет}. Тогда  — интересующее нас событие. При этом по условию
— интересующее нас событие. При этом по условию  ,
,  ,
,  и
и  . Очевидно, что
. Очевидно, что  , следовательно,
, следовательно,

Задача 1.4.Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения случайной величины 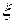 – числа возвращенных в срок кредитов из 3 выданных. Найти вероятность
– числа возвращенных в срок кредитов из 3 выданных. Найти вероятность  .
.
Решение.
В данном случае мы имеем дело с биномиальным законом с  и
и  . Случайная величина
. Случайная величина 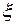 – число возвращенных в срок кредитов из трех выданных принимает значения:
– число возвращенных в срок кредитов из трех выданных принимает значения:  ,
,  ,
,  и
и  . Соответствующие им вероятности
. Соответствующие им вероятности  ,
,  ,
,  и
и  найдем, воспользовавшись формулой Бернулли:
найдем, воспользовавшись формулой Бернулли:  :
:

 ;
;

 ;
;
 .
.
Ряд распределения случайной величины 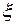 имеет вид:
имеет вид:
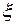 | 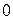 | 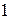 | 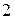 | 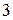 |
 |  |  |  |  |
 .
.
Задача 1.5. Негосударственный пенсионный фонд начисляет по пенсионным счетам  годовых. 1 января 2010 года вкладчик перечислил
годовых. 1 января 2010 года вкладчик перечислил  руб. Какие проценты будут начислены на эту сумму к 31 декабря 2016 года?
руб. Какие проценты будут начислены на эту сумму к 31 декабря 2016 года?
Решение.
С 1 января 2010 года до 31 декабря 2016 года пройдет  лет. По основной формуле сложных процентов к 31 декабря 2016 года на пенсионном счете будет накоплена сумма
лет. По основной формуле сложных процентов к 31 декабря 2016 года на пенсионном счете будет накоплена сумма
 .
.
Поэтому проценты составляют
 руб.
руб.
Задача 1.6. Вкладчик внес на счет  руб. Банк гарантирует, что на протяжении трех ближайших лет эффективная годовая процентная ставка будет равна
руб. Банк гарантирует, что на протяжении трех ближайших лет эффективная годовая процентная ставка будет равна 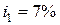 . Через три года банк установит процентную ставку
. Через три года банк установит процентную ставку 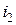 на следующие три года. Известно, что новая ставка не выйдет за пределы промежутка
на следующие три года. Известно, что новая ставка не выйдет за пределы промежутка  . Что можно сказать о сумме, которая будет накоплена за шесть лет?
. Что можно сказать о сумме, которая будет накоплена за шесть лет?
Решение.
По основной формуле сложных процентов искомое накопление есть
 .
.
Величина  не выйдет за пределы отрезка
не выйдет за пределы отрезка  . Поэтому можно гарантировать, что
. Поэтому можно гарантировать, что  .
.
Задача 1.7. Пенсионный фонд должен выплатить участнику:
1. 5000 руб. 1 июля 2009 года;
2. 3000 руб. 1 марта 2012 года;
3. 2000 руб. 1 октября 2013 года;
4. 8000 руб. 1 апреля 2015 года.
Найдите величину обязательств фонда по отношению к этому участнику на 1 января 2008 года. Техническая процентная ставка, используемая фондом для оценки своих обязательств, равна 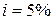 .
.
Решение.
Пусть время измеряется в годах, начиная с 1 января 2008 года, а один месяц равен  года. Тогда
года. Тогда
1. 1 июля 2009 года – это момент  ;
;
2. 1 марта 2012 года – это момент  ;
;
3. 1 октября 2013 года – это момент  ;
;
4. 1 апреля 2015 года – это момент  .
.
Коэффициент дисконтирования 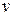 дается формулой
дается формулой
 ,
,
поэтому величина обязательств фонда на 1 января 2008 года равна:
 руб.
руб.
Задача 1.8. Эксперты негосударственного пенсионного фонда предполагают, что на протяжении ближайших пяти лет эффективная годовая процентная ставка будет равна  . На протяжении следующего пятилетия ожидается годовая процентная ставка
. На протяжении следующего пятилетия ожидается годовая процентная ставка  . Человек покупает десятилетнюю ренту с выплатой в конце каждого года 1000 руб. Подсчитайте ее стоимость.
. Человек покупает десятилетнюю ренту с выплатой в конце каждого года 1000 руб. Подсчитайте ее стоимость.
Решение.
Приведенная ценность в настоящий момент 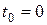 пяти годовых платежей в моменты 1, 2, 3, 4, 5 равна
пяти годовых платежей в моменты 1, 2, 3, 4, 5 равна
 ,
,
где символ  указывает эффективную годовую процентную ставку на промежутке, который рассматривается в качестве единичного, т.е.
указывает эффективную годовую процентную ставку на промежутке, который рассматривается в качестве единичного, т.е.
 руб.
руб.
Приведенная ценность в момент  пяти годовых платежей в моменты 6, 7, 8, 9, 10 равна
пяти годовых платежей в моменты 6, 7, 8, 9, 10 равна
 руб.
руб.
Чтобы привести эту сумму к моменту 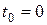 , умножим ее на
, умножим ее на  , что даст
, что даст  руб. Итак, стоимость ренты есть 3791 руб.+2616 руб.=6407 руб.
руб. Итак, стоимость ренты есть 3791 руб.+2616 руб.=6407 руб.
