Тема 3. Математическая логика
Основные понятия логики: высказывания и рассуждения. Основные логические операции и их свойства. Алгебра высказываний. Понятие о булевской алгебре; алгебра высказываний как интерпретация булевской алгебры. Логические функции и способы их задания – таблицы и формулы. Дизъюнктивные и конъюнктивные формы. Теорема о функциональной полноте. Исчисление высказываний. Понятие об алфавите, формулах, аксиомах, правилах вывода и основных теоремах исчисления высказываний. Логика предикатов. Предметная область и предметные переменные. Кванторы общности и существования. Свободные и связанные переменные. Эквивалентные соотношения в логике предикатов. Общезначимые и противоречивые формулы. Запись утверждений естественного языка в логике предикатов. Понятие об исчислении предикатов ([1, часть 1, кроме § 11]; [2, разд. 1.4,1.5]; [3, § 13.1 – 13.3]).
При изучении темы следует усвоить основные понятия алгебры логики: высказывание (предположение, которое может быть истинно или ложно, при этом логическая переменная х равна соответственно 1 или 0), логические операции (логические связки) с помощью которых строятся новые высказывания, образующие формулы алгебры логики (алгебры высказываний), таблицы истинности таких высказываний.
Надо четко знать основные логические операции: отрицание высказывания Х (высказывание 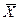 , которое истинно, когда Х ложно, и ложно, когда Х – истинно), конъюнкция (дизъюнкция) двух высказываний Х и Y (высказывание
, которое истинно, когда Х ложно, и ложно, когда Х – истинно), конъюнкция (дизъюнкция) двух высказываний Х и Y (высказывание 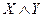 (
( 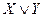 ), которое истинно (ложно) тогда и только тогда, когда Х и Y истинны (ложны)), импликация (эквивалентность) двух высказываний Х и Y (высказывание
), которое истинно (ложно) тогда и только тогда, когда Х и Y истинны (ложны)), импликация (эквивалентность) двух высказываний Х и Y (высказывание 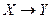 (
( 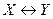 ), которое ложно (истинно) тогда и только тогда, когда Х истинно, а Y ложно (Х и Y оба истинны или оба ложны)).
), которое ложно (истинно) тогда и только тогда, когда Х истинно, а Y ложно (Х и Y оба истинны или оба ложны)).
В табл. 1 и 2 приводятся таблицы истинности этих высказываний.
Таблица 1
| Х | Отрицание 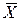 |
Таблица 2
| Х | Y | Конъюнкция 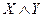 | Дизъюнкция 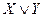 | Импликация 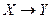 | Эквивалентность 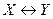 |
Логические операции высказываний тесно связаны с операциями над множествами. Отрицание высказывания соответствует дополнению множества, конъюнкция и дизъюнкция высказываний – пересечению и объединению множеств, импликация – включению подмножества в множество, эквивалентность высказываний – равенству множеств.
Студент должен также представлять основные производные логические операции: штрих Шеффера 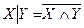 (антиконъюнкция), стрелка Пирса
(антиконъюнкция), стрелка Пирса 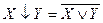 (антидизъюнкция), сумма по модулю два
(антидизъюнкция), сумма по модулю два 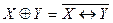 (антиэквивалентность).([1, часть 1, § 3]; [2, § 13.1]). Уметь устанавливать эквивалентность (равносильность), наличие отношения следствия двух высказываний с помощью таблиц истинности.
(антиэквивалентность).([1, часть 1, § 3]; [2, § 13.1]). Уметь устанавливать эквивалентность (равносильность), наличие отношения следствия двух высказываний с помощью таблиц истинности.
Следует отметить, что составление таблиц истинности различных высказываний является наилучшим способом запоминания определений логических операций.
Пример 4. С помощью таблиц истинности проверить эквивалентность формул: 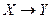 ,
, 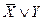 и
и 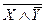 .
.
Р е ш е н и е. Составим таблицу истинности для данных формул (см. табл. 1, 2).
| Х | Y | 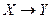 | 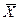 | 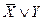 | 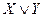 | 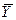 | 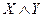 | 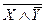 |
Сравнивая 3-й, 5-й и 9-й столбцы, убеждаемся в эквивалентности рассматриваемых формул. ►
Студенту необходимо освоить основные свойства логических операций: идемпотентность (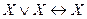 ,
, 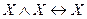 ),коммутативность (
),коммутативность ( 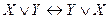 ,
, 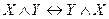 ), ассоциативность (
), ассоциативность (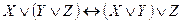 ,
, 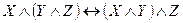 ), дистрибутивность (
), дистрибутивность (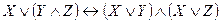 ,
,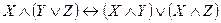 ),двойное отрицание(
),двойное отрицание( 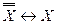 ), законы де Моргана(
), законы де Моргана( 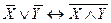 ,
, 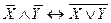 ), поглощение (
), поглощение ( 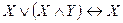 ,
, 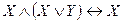 ), исключение третьего (
), исключение третьего ( 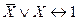 ), противоречие (
), противоречие ( 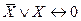 ) и другие. Уметь использовать эти свойства для упрощения формул алгебры логики. С этой целью часто используются следующие эквивалентные соотношения[4]
) и другие. Уметь использовать эти свойства для упрощения формул алгебры логики. С этой целью часто используются следующие эквивалентные соотношения[4] 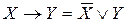 ,
, 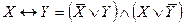 ,
, 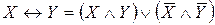 и другие.
и другие.
Пример 5. Упростить формулу 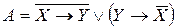 .
.
Р е ш е н и е. Используя дважды правило исключения импликации ( 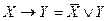 – см. пример 4), получим
– см. пример 4), получим 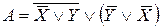 . Применяя законы де Моргана, двойного отрицания, ассоциативности и поглощения, получим
. Применяя законы де Моргана, двойного отрицания, ассоциативности и поглощения, получим 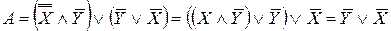 . ►
. ►
Непустое множество М любой природы 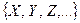 , в котором определены отношение «=» (равно) и три операции «+» (сложение), « · » (умножение) и «–» (отрицание), подчиняющиеся коммутативным, ассоциативным, дистрибутивным законам, законам идемпотентности, двойного отрицания, де-Моргана и поглощения, называется булевой алгеброй. Если под основными элементами Х, Y, Z… подразумевать высказывания, под операциями «+», « · », «–» дизъюнкцию, конъюнкцию, отрицание соответственно, то алгебра высказываний есть интерпретация (модель) булевой алгебры.
, в котором определены отношение «=» (равно) и три операции «+» (сложение), « · » (умножение) и «–» (отрицание), подчиняющиеся коммутативным, ассоциативным, дистрибутивным законам, законам идемпотентности, двойного отрицания, де-Моргана и поглощения, называется булевой алгеброй. Если под основными элементами Х, Y, Z… подразумевать высказывания, под операциями «+», « · », «–» дизъюнкцию, конъюнкцию, отрицание соответственно, то алгебра высказываний есть интерпретация (модель) булевой алгебры.
При рассмотрении формул алгебры логики важно установить, является ли данная формула тождественно истинной (тавтологией), тождественно ложной (противоречием) или выполнимой. В первом случае формула принимает значение 1, во втором случае – значение 0 при любых значениях входящих в нее переменных, в третьем случае – принимает значение 1 хотя бы при одном наборе значений переменных.
Пример 6. Установить вид формулы алгебры логики
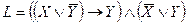 .
.
Р е ш е н и е. Используя определение логических операций (табл. 1, 2), составим таблицу истинности формулы L:
| Х | Y | 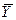 | 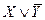 | 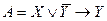 | 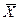 | 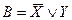 | 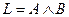 |
Из полученной таблицы видно, что формула L является выполнимой, так как она принимает значение 1, но не является тождественно выполнимой (тавтологией), ибо при определенных значениях высказываний она принимает значение 0. ►
Методы алгебры логики могут быть использованы при решении логических задач. Имея конкретные условия логической задачи, стараются записать их в виде формул алгебры логики. Далее, упрощая полученную формулу, составляя ее таблицу истинности, удается найти ответ на вопрос задачи (см., например, [1, 1-е практическое занятие, задача 4], [2, пример 13.4]).
При изучении булевых (логических) функций (в которой сами функции и каждая из ее переменных принимают одно из двух значений 0 или 1) следует обратить внимание на то, что для них справедливы свойства, аналогичные свойствам высказываний.
Каждая булева функция 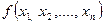 может быть представлена в виде дизъюнктивной нормальной формы (ДНФ) и конъюнктивной нормальной формы (КНФ). ДНФ (КНФ) формулы алгебры логики есть дизъюнкция (конъюнкция) элементарных конъюнкций (дизъюнкций), представляющих конъюнкции (дизъюнкции) переменных
может быть представлена в виде дизъюнктивной нормальной формы (ДНФ) и конъюнктивной нормальной формы (КНФ). ДНФ (КНФ) формулы алгебры логики есть дизъюнкция (конъюнкция) элементарных конъюнкций (дизъюнкций), представляющих конъюнкции (дизъюнкции) переменных 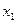 ,
, 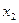 , …,
, …, 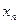 или их отрицаний. Любая булева функция может иметь много представлений в виде ДНФ и КНФ, среди которых особое место занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ), которые согласно теореме о функциональной полноте, единственны для любой булевой функции, отличной от константы 0 (для СДНФ) и отличной от константы 1 (для СКНФ).
или их отрицаний. Любая булева функция может иметь много представлений в виде ДНФ и КНФ, среди которых особое место занимают совершенные ДНФ (СДНФ) и совершенные КНФ (СКНФ), которые согласно теореме о функциональной полноте, единственны для любой булевой функции, отличной от константы 0 (для СДНФ) и отличной от константы 1 (для СКНФ).
СДНФ и СКНФ не содержат двух одинаковых элементарных конъюнкций (дизъюнкций), ни одна конъюнкция (дизъюнкция) не содержит одновременно двух одинаковых переменных; а также переменную и ее отрицание. При этом каждая конъюнкция (дизъюнкция) включает либо переменную 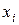 , либо ее отрицание для всех переменных, входящих в формулу.
, либо ее отрицание для всех переменных, входящих в формулу.
Одним из способов построения СДНФ и СКНФ является способ, основанный на использовании таблицы истинности булевой функции.
Для построения СДНФ (СКНФ) для каждого набора значений переменных, на которых булева функции равна 1 (равна 0), выписывают конъюнкции (дизъюнкции) переменных: над теми переменными, которые на этом наборе равны 0 (равны 1), ставятся отрицания, и все такие конъюнкции (дизъюнкции) соединяются знаками дизъюнкций (конъюнкций).
Пример 7. Найти СДНФ и СКНФ булевой функции 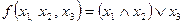 .
.
Р е ш е н и е. Составим таблицу истинности функции 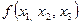 .
.
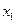 | 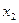 | 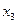 | 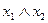 | 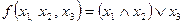 |
1) Функция 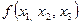 равна 1 на наборах
равна 1 на наборах 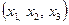 : (0; 0; 1), (0; 1; 1), (1; 0; 1), (1; 1; 0), (1; 1; 1), т.е. соответствующие конъюнкции (над равными 0 переменными ставим знак отрицания)
: (0; 0; 1), (0; 1; 1), (1; 0; 1), (1; 1; 0), (1; 1; 1), т.е. соответствующие конъюнкции (над равными 0 переменными ставим знак отрицания) 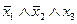 ,
, 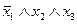 и т.д. Соединяя их знаками дизъюнкции, получим СДНФ функции:
и т.д. Соединяя их знаками дизъюнкции, получим СДНФ функции:
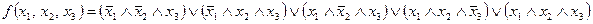 .
.
2) Функция 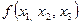 равна 0 на наборах
равна 0 на наборах 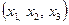 : (0; 0; 0), (0; 1; 0), (1; 0; 0), т.е. соответствующие дизъюнкции (над равными 1 переменными ставим знак отрицания)
: (0; 0; 0), (0; 1; 0), (1; 0; 0), т.е. соответствующие дизъюнкции (над равными 1 переменными ставим знак отрицания) 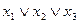 ,
, 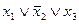 ,
, 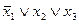 . Соединяя их знаками конъюнкции, получим СКНФ функции:
. Соединяя их знаками конъюнкции, получим СКНФ функции:
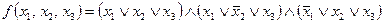 .►
.►
Система булевых функций является полной, если любая функция может быть выражена через функции этой системы с помощью суперпозиций. Так, система функций { 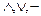 }является полной, ибо произвольную булеву функцию можно представить через конъюнкцию, дизъюнкцию и отрицание.
}является полной, ибо произвольную булеву функцию можно представить через конъюнкцию, дизъюнкцию и отрицание.
Алгебра высказываний использует логические значения высказываний (истина, ложь), не являющиеся математическими понятиями. В связи с этим желательно построить формальную математическую логику, не пользуясь понятиями истинности и ложности.
Исчисление высказываний – аксиоматическая логическая система, интерпретацией (моделью) которой является алгебра высказываний. Здесь мы вновь встречаемся с формулами алгебры логики. Однако теперь формулы рассматриваются не как способ представления функций, а как составные высказывания, образованные из элементарных высказываний (переменных) с помощью основных логических связок.
Из всех формул алгебры высказываний выделяется часть формул, объявляемых аксиомами. Определяется некоторое правило, по которому их одних формул можно получать новые. Аксиомы выделяются, а правило определяется так, что по нему из аксиом могут быть получены все тождественно-истинные высказывания (тавтологии) и только они. Получение тавтологий алгебры высказываний, представленных в виде теорем, является основной задачей исчисления высказываний. Подробнее материал об исчислении высказываний см, например, [4, §6.1].
При изучении предикатов необходимо четко понимать, что они представляют предложения, содержащие предметные переменные, при замене которых конкретными значениями (элементами) рассматриваемых множеств они обращаются в высказывания, принимающие значения «истинно» или «ложно». Например, предикат Р(х) «х2=9» представляет истинное высказывание при х=± 3 и – ложное при х≠ ±3.
Особое внимание следует уделить кванторным операциям, применимым к предикатам. Знать определение квантора общности (квантора существования) – правила, которое каждому предикату 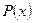 , определенному на множестве Х, сопоставляет высказывание, обозначаемое
, определенному на множестве Х, сопоставляет высказывание, обозначаемое 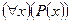 (или
(или 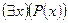 , которое истинно тогда и только тогда, когда предикат
, которое истинно тогда и только тогда, когда предикат 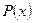 истинен для всех (хотя бы для одного) значений(я) из Х. Переход от
истинен для всех (хотя бы для одного) значений(я) из Х. Переход от 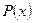 к
к 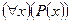 или
или 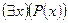 называется связыванием переменной х, или навешиванием квантора на переменную х.
называется связыванием переменной х, или навешиванием квантора на переменную х.
При рассмотрении 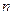 - местных предикатов, содержащих
- местных предикатов, содержащих 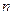 предметных переменных, студент должен понимать смысловое отличие, например, предикатов
предметных переменных, студент должен понимать смысловое отличие, например, предикатов 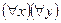 (
( 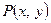 ),
), 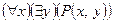 ,
, 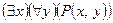 ,
, 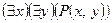 .
.
Две формулы логики предикатов называется равносильными, если они принимают одинаковые логические значения при всех значениях входящих в них переменных. Обращаем внимание на ряд правил перехода от одних формул к другим, им равносильным:
– перенос квантора через отрицание (например 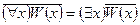 ,
, 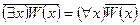 ;
;
– вынос квантора за скобки (например, 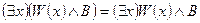 ,
, 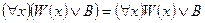 , В – не содержит х);
, В – не содержит х);
– перестановка одноименных кванторов (например, 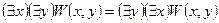 );
);
– переименование связанных кванторов (например, 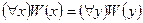 ).
).
Аналогично тому, как было построено исчисление высказываний, может быть построено и исчисление предикатов. Вывод системы аксиом высказываний, как и в случае исчисления высказываний, может осуществляться по-разному. Например, можно взять систему аксиом исчисления высказываний с добавлением двух предикатных аксиом и добавить соответствующие правила введения кванторов общности и существования [4, §6.3].
Следует отметить, что в алгебре высказываний использование таблиц истинности давало достаточно эффективный способ решений вопроса о том, является или данная формула тождественно истинной (тавтологией). В логике предикатов нет эффективного способа решения вопроса о том, являет-ся ли любая рассматриваемая формула общезначимой (всегда выполнимой). В связи с этим аксиоматический подход здесь становится необходимым.
Тема 4. Теория графов
Основные определения: неориентированные и ориентированные графы, мультиграфы и кратные ребра. Смежность и инцидентность. Способы представления графов. Матрицы смежности и инцидентности. Операции над графами. Графы и бинарные отношения. Изоморфизм графов. Полные графы и клики. Пути, циклы, цепи, простые цепи в неориентированных графах. Связность и компоненты связности. Расстояния. Центр, радиус, диаметр графа. Обходы графов. Виды связности в ориентированных графах: сильная связность, односторонняя связность. Двудольные графы и формулировка задачи о паросочетаниях. Знаковые графы и понятие стабильности. Применение знаковых графов для формализации задач в социальной сфере. Деревья и их свойства. Цикломатическое число. Направленные деревья. Приложения деревьев: иерархии, классификации. Обходы деревьев. ([1, часть 5]; [2, разд. 7.1,7.2]; [3, § 14.1, 14.2]).
Основные понятия теории графов
Графом G (V, E) называется конечное непустое множество вершин V и конечное множество ребер E. Каждое ребро связывает пару вершин. Если ребро e соединяет вершины 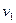 и
и 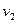 , то говорят, что ребро e и вершины
, то говорят, что ребро e и вершины 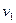 ,
, 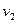 инцидентны.
инцидентны.
Два ребра, связывающие одну и ту же пару вершин 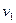 и
и 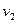 , называются кратными; ребро, связывающее вершину саму с собой, называется петлей.
, называются кратными; ребро, связывающее вершину саму с собой, называется петлей.
Степенью вершины графа называется число ребер графа, инцидентных этой вершине (петли считаются дважды). Степень вершины v обозначается d(v). Вершина степени 0 называется изолированной, вершина степени 1 – висячей. Вершина графа называется четной, если ее степень четна, и нечетной, если нечетна.
Поскольку ребро, соединяющее вершины 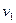 и
и 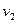 , добавляет по единице в степени этих ребер
, добавляет по единице в степени этих ребер 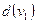 и
и 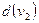 , справедливо соотношение:
, справедливо соотношение: 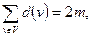 где m – количество ребер графа.
где m – количество ребер графа.
Граф называется полным, если каждые две различные его вершины соединены одним и только одним ребром.
Матрицей смежности графа G(V, E) называется квадратная матрица А(G) n-го порядка (n – число вершин) с элементами:
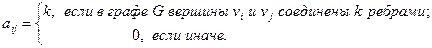
Если в графе нет петель, то на главной диагонали матрицы смежности стоят нули. Если же в графе нет кратных ребер, то все элементы матрицы равны либо нулю, либо единице.
Матрицей инцидентности графа G(V, E) называется матрица В(G) размера 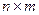 (n – число вершин, m – число ребер) с элементами:
(n – число вершин, m – число ребер) с элементами:
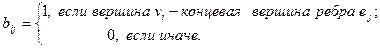
Пример 8. Для графа, изображенного на рисунке 2, построить матрицы смежности и инцидентности.
 Р е ш е н и е. Начнем с построения матрицы смежности А(G). У данного графа пять вершин, следовательно, матрица смежности будет иметь размер 5×5. Поскольку у графа есть петля и она находится в первой вершине, то на главной диагонали элемент
Р е ш е н и е. Начнем с построения матрицы смежности А(G). У данного графа пять вершин, следовательно, матрица смежности будет иметь размер 5×5. Поскольку у графа есть петля и она находится в первой вершине, то на главной диагонали элемент 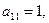 а все остальные
а все остальные 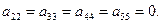
Ребро 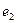 соединяет первую и вторую вершины; других ребер, соединяющих эти же вершины, нет, следовательно, элементы
соединяет первую и вторую вершины; других ребер, соединяющих эти же вершины, нет, следовательно, элементы 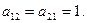 Аналогично,
Аналогично, 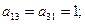
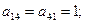
Рис. 2
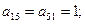
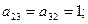
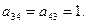 Ребра
Ребра 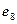 и
и 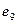 соединяют четвертую и пятую вершины и являются кратными, поэтому
соединяют четвертую и пятую вершины и являются кратными, поэтому 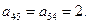 Все остальные элементы
Все остальные элементы 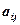 равны нулю.
равны нулю.
Таким образом, матрица смежности имеет вид:
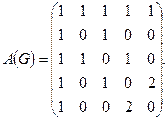
Теперь построим матрицу инцидентности В(G). Так как у графа 5 вершин и 9 ребер, матрица В(G) будет размера 5×9. Первое ребро – это петля в первой вершине, поэтому в первом столбце, который соответствует первому ребру, только один элемент 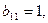 а все остальные нулевые.
а все остальные нулевые.
Второе ребро соединяет первую и вторую вершины, следовательно, 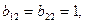 а остальные элементы второго столбца – нулевые. Рассуждая аналогично, получаем матрицу инцидентности:
а остальные элементы второго столбца – нулевые. Рассуждая аналогично, получаем матрицу инцидентности:
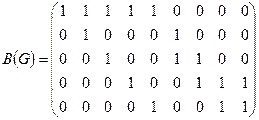 . ►
. ►
Ориентированные графы
Направленные ребра графа, т.е. ребра, для которых определены вершины, из которых они выходят, и вершины, в которые входят, называются дугами. Если все ребра графа направлены, то он называется ориентированным или орграфом.
Матрицей смежности ориентированного графа G(V, E) называется квадратная матрица А(G) n-го порядка (n – число вершин) с элементами:
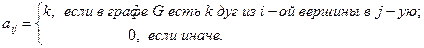
Матрицей инцидентности ориентированного графа G(V, E) называется матрица В(G) размера 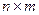 (n – число вершин, m – число ребер) с элементами:
(n – число вершин, m – число ребер) с элементами:
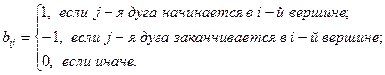
Пример 9. Построить орграфы по матрицам смежности и инцидентности:
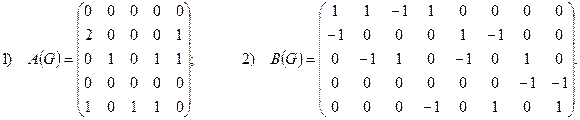
 Р е ш е н и е. 1) Даная матрица смежности – квадратная матрица пятого порядка, следовательно, у рассматриваемого графа пять вершин. Первая и четвертая строки смежной матрицы нулевые, т.е. из первой и четвертой вершин не выходит ни одной дуги. Во второй строке два элемента отличны от нуля, причем,
Р е ш е н и е. 1) Даная матрица смежности – квадратная матрица пятого порядка, следовательно, у рассматриваемого графа пять вершин. Первая и четвертая строки смежной матрицы нулевые, т.е. из первой и четвертой вершин не выходит ни одной дуги. Во второй строке два элемента отличны от нуля, причем, 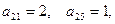 следовательно, из второй вершины выходят три дуги: две в первую вершину и одна в пятую (рис. 3).
следовательно, из второй вершины выходят три дуги: две в первую вершину и одна в пятую (рис. 3).
Рис. 3
В третьей и пятой строках по три единицы: 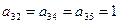 и
и 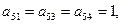 т.е. из третьей и пятой вершин выходят по три дуги: из третьей вершины – во вторую, четвертую и пятую вершины, а из пятой вершины – в первую, третью и четвертую.
т.е. из третьей и пятой вершин выходят по три дуги: из третьей вершины – во вторую, четвертую и пятую вершины, а из пятой вершины – в первую, третью и четвертую.
2) Матрица инцидентности имеет размерность 5×8, т.е. у искомого графа пять вершин и восемь дуг. В первом столбце 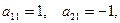 следовательно, первое ребро выходит из первой вершины и входит во вторую. Второе ребро выходит из первой вершины и входит в третью и т.д. Искомый граф представлен на рисунке 4. ►
следовательно, первое ребро выходит из первой вершины и входит во вторую. Второе ребро выходит из первой вершины и входит в третью и т.д. Искомый граф представлен на рисунке 4. ►
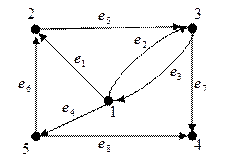


Рис. 4 Рис. 5
Пример 10. На множестве V ={1; 3; 5; 7; 9} задано отношение 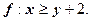 Построить орграф данного отношения.
Построить орграф данного отношения.
Р е ш е н и е. Пусть элементы множества V ={1; 3; 5; 7; 9} будут вершинами графа. Будем считать, что из вершины x проведена дуга в вершину y, если выполнено неравенство 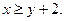
Из вершины, соответствующей числу 1, не выходит ни одна дуга (рис. 5), поскольку среди элементов множества V нет таких, что 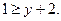
Из вершины, соответствующей числу 3, будет выходить ровно одна дуга в вершину 1, поскольку для остальных элементов множества V неравенство 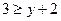 не выполнено. Аналогично, из вершин 5, 7 и 9 будут выходить соответственно две, три и четыре дуги. ►
не выполнено. Аналогично, из вершин 5, 7 и 9 будут выходить соответственно две, три и четыре дуги. ►
Операции над графами
Граф G′ = (V′, E′), вершины и ребра которого являются вершинами и ребрами графа G (V, E), т.е. 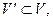
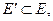 называется подграфом графа G.
называется подграфом графа G.
Подграф G′ = (V′, E′) графа G (V, E), являющийся полным графом, называется кликой. Максимальная клика — это клика с максимально возможным числом вершин среди всех существующих клик графа.
У графа, изображенного на рис. 2, существует несколько клик, например, 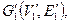 где
где 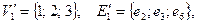 или
или 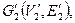 где
где 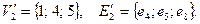 Однако клики с четырьмя вершинами в этом графе нет, поскольку для ее существования необходимо, чтобы было четыре вершины со степенью три (без учета кратных ребер), а в данном графе таких вершин только три: первая, третья и четвертая.
Однако клики с четырьмя вершинами в этом графе нет, поскольку для ее существования необходимо, чтобы было четыре вершины со степенью три (без учета кратных ребер), а в данном графе таких вершин только три: первая, третья и четвертая.
Дополнением графа G(V, E) называется граф 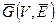 , множество вершин которого совпадает с множеством вершин исходного графа, а множество ребер является дополнением множества E, т.е.
, множество вершин которого совпадает с множеством вершин исходного графа, а множество ребер является дополнением множества E, т.е. 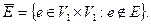
Объединением графов 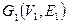 и
и 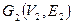 таких, что
таких, что 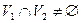 и
и 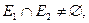 называется граф
называется граф 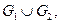 множеством вершин которого является множество
множеством вершин которого является множество 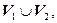 а множеством ребер – множество
а множеством ребер – множество 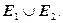
Пересечением графов 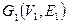 и
и 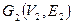 называется граф
называется граф 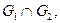 множеством вершин которого является множество
множеством вершин которого является множество 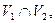 а множеством ребер – множество
а множеством ребер – множество