Последовательность решения. 1. Развертку призмы выполняем по чертежу задачи 5
1. Развертку призмы выполняем по чертежу задачи 5. Так как призма прямая, то на горизонтальную плоскость проекций ее основание проецируется без искажения, следовательно, длины боковых граней будем измерять по проекции основания призмы. Высота боковых граней равна высоте призмы на фронтальной плоскости проекций, и положение точек линии пересечения по высоте также измеряется на фронтальной плоскости проекций.
2. Строим развертку призмы. На свободном месте поля чертежа проводим горизонтальную линию и на ней откладываем точку k. Затем, последовательно измеряя длины граней, пристраиваем их друг к другу, т.е. ke , затем eu, потом ug и gk. Из каждой точки поднимаем высоту призмы и соединяем полученные точки до прямоугольника, т. е. получили развертку боковой поверхности призмы.
3. Наносим линию пересечения. Для этого определяем положение точек линии пересечения на гранях. Например, измеряем расстояние от точки k до точки 1 на горизонтальной проекции и откладываем это расстояние на развертке грани ke от точки k, затем поднимаемся на высоту точки 1, измеряя ее на фронтальной проекции призмы от основания до точки 1' (измерять надо обязательно перпендикулярно к основанию призмы). Откладываем точки е1 и е2 на ребре е. Достраиваем все точки и соединяем их в той же последовательности, что и на чертеже задачи 5. На грани ug соединяем точки 4, 5, 6, на гранях ke и eu последовательно соединяем точки 1, е1, 3, 2, е2, 1.
4. Для построения развертки пирамиды необходимо найти натуральные величины ребер пирамиды. Рассмотрим ребро с'd'. Оно расположено параллельно оси ОХ, следовательно, горизонтальная проекция ребра сd есть истинная величина. Натуральную величину ребер ab и bc находим методом вращения, для этого разворачиваем их относительно точки b до положения, параллельного оси ОХ на горизонтальной плоскости проекций, точки а и с займут новое положение а1 и с1. Из полученных точек поднимаем линии связи до пересечения с линиями связи, исходящими из точек а' и с' (линии перемещаются параллельно оси ОХ). Полученные точки а1' и с1' соединяем с точкой b' получим истинные величины ребер.
5. Натуральную величину ребра ас находим методом прямоугольного треугольника. Из точки с на горизонтальной плоскости проекций проводим перпендикуляр к ребру ас и от точки с откладываем разницу координат Zа – Zс = Zа-с. Отмечаем точку с2 и соединяем ее с точкой а, получим истинную величину ребра АС. Аналогично находим натуральные величины ребер ad и db. На фронтальной плоскости проекций из точки d' восставляем перпендикуляр к ребру d'b' и откладываем на нем от точки d' разницу координат Yb – Yd = dY1, отмечаем точку d1' , соединяем с точкой b', получим натуральную величину ребра BD. Таким же способом находим истинную величину ребра АD, только разницу координат берем между точками a и d: Ya – Yd =d Y2.
6. Фиксируем точки е1' и е2' через пересекающиеся линии. Продлеваем линию 3'е1' до пересечения со стороной b'c', так как точка е1' принадлежит грани b'c'd', отмечаем точку 9'. Тогда точка е1’ будет лежать на пересечении линий 1'7' и 3'9'. Для точки е2’ продлеваем линию 2'е2' и отмечаем точку 10' на ребре a'b'. Все точки находим на натуральных величинах ребер.
7. Построив все натуральные величины ребер пирамиды, последовательно выстраиваем ее развертку. Отмечаем точку d (произвольно на свободном месте поля чертежа) и строим прямую, на которой откладываем отрезок dc. Затем методом засечек строим точку b: для этого радиусом, равным св, из точки с проводим дугу, из точки d радиусом dc проводим дугу. Место пересечения дуг отмечаем точкой b. Так последовательно достраиваем все боковые грани пирамиды и ее основание.
8. На построенные ребра развертки пирамиды наносим точки и соединяем их между собой так, как они соединены в задаче 5.
Задача № 7
Построить пересечение сферы (с центром в точке O и радиусом R) с призматическим отверстием ABCD. Решение задачи показать в трех проекциях. Данные берут из таблицы 4.
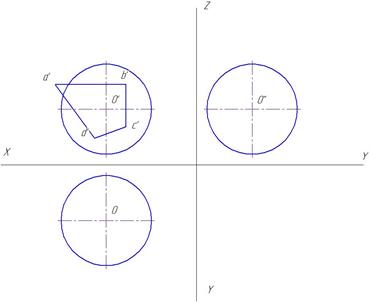
Указания к решению задачи № 7.
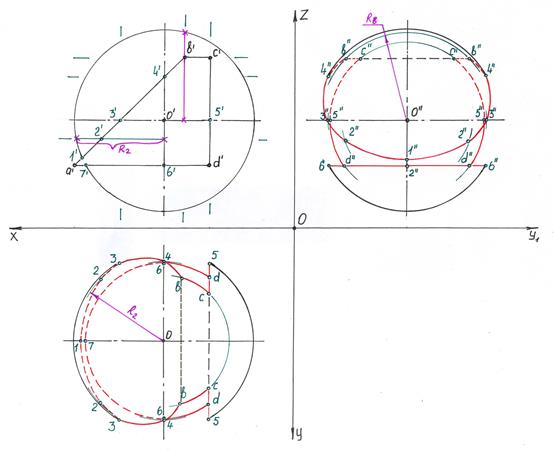
Вырожденная фронтальная проекция сквозного отверстия представлена четырехугольником ABCD. Задача сводится к построению линии пересечения граней четырехугольника ABCD с поверхностью сферы. В сечении плоскости со сферой всегда получается окружность, которая может проецироваться или в окружность, или в эллипс, в зависимости от положения ее плоскости по отношению к плоскости проекций. Обратить особое внимание к нахождению точек кривых, определяющих границы видимости кривых и точки касания эллипсов с очерковыми окружностями сферы.
Таблица 4. Данные к задаче № 7
| Номер варианта | XО | Yo | ZО | XA | ZA | XВ | ZВ | XС | ZС | XD | ZD | R |
Пример решения задачи