Раздел 2. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ 1 страница
Предмет статистической (молекулярной) физики и термодинамики.
Тема 6. Макроскопические состояния
6.1. Тепловое движение. Макроскопические параметры. Равновесные состояния и процессы, их изображения на термодинамических диаграммах. Интенсивные и экстенсивные параметры.
6.2. Идеальный газ. Уравнение молекулярно-кинетической теории идеальных газов для давления. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры.
6.3. Уравнение состояния идеального газа (Менделеева - Клапейрона). Изопроцессы и их уравнения. Законы Дальтона и Авогадро.
6.4. Число степеней свободы молекул. Закон равномерного распределения энергии по степеням свободы молекул.
6.5. Закон Максвелла для распределения молекул по скоростям и энергиям теплового движения. Средняя арифметическая и наиболее вероятная скорости теплового движения молекул.
6.6. Барометрическая формула. Распределение Больцмана для частиц во внешнем силовом поле.
6.7. Эффективное сечение рассеяния. Среднее число столкновений и длина свободного пробега молекул.
6.8. О явлениях переноса в термодинамических неравновесных системах. Опытные законы диффузии, теплопроводности и внутреннего трения. Молекулярно-кинетическая теория этих явлений.
Тема 7. Основы термодинамики и ее связь с молекулярно-кинетической теорией идеальных газов
7.1. Внутренняя энергия. Количество теплоты. Работа газа при изменении его объема. Первое начало термодинамики.
7.2. Теплоемкость многоатомных газов. Зависимость теплоемкости идеального газа от вида процесса.
7.3. Применение 1-го начала термодинамики к изопроцессам и адиабатическому процессу идеального газа.
7.4. Обратимые и необратимые процессы. Круговой процесс (цикл). Тепловые двигатели и холодильные машины.
7.5. Цикл Карно. Максимальный кпд тепловой машины. Независимость кпд цикла Карно от природы рабочего тела. Второе начало термодинамики.
7.6. Энтропия, ее статистическое толкование. Порядок и беспорядок в природе. Энтропия и второе начало термодинамики. Третье начало термодинамики (теорема Нернста). Термодинамические функции состояния.
7.7. Отступление от законов идеальных газов. Реальные газы. Уравнение Ван-дер-Ваальса и его анализ. Изотермы Ван-дер-Ваальса. Фазы и фазовые превращения. Условия равновесия фаз. Критическое состояние (точка).
7.8. Силы и потенциальная энергия межмолекулярного взаимодействия. Внутренняя энергия реального газа. Эффект Джоуля - Томпсона.
7.9. Фазовые переходы I и II рода. Диаграммы состояния. Уравнение Клапейрона - Клаузиуса.
7.10. Макросистемы вдали от равновесия. Идеи синергетики.
Список литературы
Основная литература
1. Трофимова Т.И. Курс физики. – М.: Высшая школа, 2003.
2. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Изд.центр «Академия», 2003.
3. Савельев И.В. Курс физики. Т.1-3. – М.: Наука, 1989.
4. Епифанов Г.И. Физика твердого тела. - М.: Высшая школа, 1977.
Электронная учебно – методическая литература
1. Козел С.М., Соболева Н.Н. Учебный компьютерный курс «Открытая физика 1.1». Долгопрудный: ООО «ФИЗИКОН», 2001.
Дополнительная литература
1. Суханов Л.Д. Фундаментальный курс физики. – М.: Агор, 1996, Т.1.
2. Орир Дж. Физика. Т.1-2. – М.: Мир, 1981, т.1-2.
3. Бордовский Г.А., Бурсиан Э.В. Общая физика: Курс лекций. Т.1,2. – М.: Владос. Пресс, 2001.
4. Кибец И.Н., Кибец В.И. Физика: Справочник. - Харьков: Фолио, 1997.
5. Окунь Л.Б. Физика элементарных частиц. – М.: Наука, 1988.
6. Бутиков Е.Н. Оптика. – М.: Высшая школа, 1987.
7. Широков Ю.М., Юдин Н.П. Ядерная физика. – М.: Наука, 1980.
8. Эбелинг В., Энгель А., Файстель Р. Физика процессов эволюции (синергетический подход). – М.: Эдиториал УРСС, 2001.
9. Мотылева Л.С., Скоробогатов В.А., Судариков А.М. Концепции современного естествознания. – СПб.: Союз, 2000.
Сборники задач
1. Трофимова Т.И. Сборник задач по курсу физики. – М.: Высшая школа, 1996.
2. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Изд-во физ.-мат. литературы, 2003.
3. Трофимова Т.И., Павлова З.Г. Сборник задач по курсу физики с решениями. – М.: Высшая школа, 1995.
4. Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: Книжный мир, 2004.
5. Иродов И.Е. Задачи по общей физике. – М.: Наука, 1988.
6. Волкова Е.А., Попов А.М., Рахимов А.Т. Квантовая механика на персональном компьютере. – М.: УРСС, 1995.
| 3. Основные формулы | ||
| Средняя скорость материальной точки | ||
| в векторном виде: | 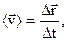 | |
в скалярном виде: где 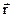 - радиус-вектор точки; - радиус-вектор точки; 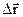 - вектор перемещения точки за промежуток времени - вектор перемещения точки за промежуток времени 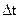 ; ; 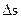 - путь, пройденный точкой за промежуток времени - путь, пройденный точкой за промежуток времени 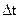 . . | 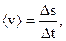 | |
| Мгновенная скорость материальной точки | ||
| в векторном виде: | 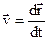 | |
| в скалярном виде: | 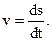 | |
| Среднее ускорение материальной точки | 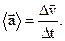 | |
| Мгновенное ускорение материальной точки | 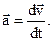 | |
| Полное ускорение при криволинейном движении | ||
| в векторном виде: | 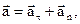 | |
| в скалярном виде: | 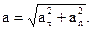 | |
| Тангенциальное ускорение | 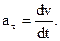 | |
| Нормальное ускорение где R – радиус кривизны траектории в данной точке. | 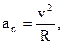 | |
Путь и скорость для равнопеременного прямолинейного движения где 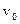 - начальная скорость. - начальная скорость. | 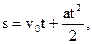 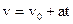 | |
| Угловая скорость в векторном виде: | 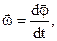 | |
в скалярном виде: где 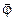 - угловое перемещение. - угловое перемещение. | 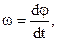 | |
| Угловое ускорение в векторном виде: | 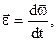 | |
| в скалярном виде: | 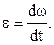 | |
Связь угловой скорости с периодом и частотой вращения где Т - период, 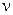 - частота вращения, N - число оборотов, совершаемых телом за время t. - частота вращения, N - число оборотов, совершаемых телом за время t. | 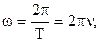 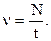 | |
Угловое перемещение и угловая скорость для равнопеременного вращательного движения где 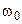 - начальная скорость. - начальная скорость. | 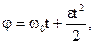 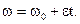 | |
| Связь между линейными и угловыми величинами где R - радиус кривизны траектории. | 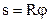 , , 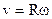 , , 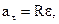 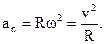 | |
| Уравнение динамики поступательного движения материальной точки (II закон Ньютона) | 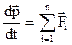 | |
| или | 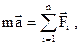 | |
где 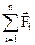 - геометрическая сумма сил, действующих на материальную точку; m – масса, - геометрическая сумма сил, действующих на материальную точку; m – масса, 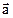 - ускорение, - ускорение, 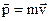 - импульс точки. - импульс точки. | ||
Сила тяжести где 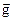 – ускорение свободного падения. – ускорение свободного падения. | 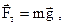 | |
| Сила гравитационного взаимодействия где G – гравитационная постоянная, m1 и m2 массы взаимодействующих тел, находящихся на расстоянии R друг от друга. | 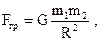 | |
| Сила упругости где k - коэффициент упругой силы (коэффициент жесткости - в случае пружины); х - абсолютная деформация. | 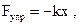 | |
Сила трения скольжения где 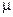 - коэффициент трения скольжения; N - сила нормального давления. - коэффициент трения скольжения; N - сила нормального давления. | 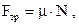 | |
Координаты центра масс системы материальных точек где 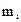 - масса i-й материальной точки; - масса i-й материальной точки; 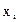 , , 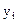 , , 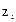 - ее координаты. - ее координаты. | 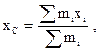 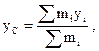 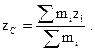 | |
Момент силы относительно оси вращения (При условии, что сила 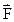 , действующая на тело, лежит в плоскости перпендикулярной оси вращения ). Здесь L - плечо силы , действующая на тело, лежит в плоскости перпендикулярной оси вращения ). Здесь L - плечо силы 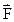 (кратчайшее расстояние от оси вращения до линии действия силы). (кратчайшее расстояние от оси вращения до линии действия силы). | 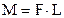 . . | |
| Момент инерции относительно оси вращения | ||
| материальной точки где m – масса точки; r - расстояние от оси вращения; | 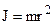 , , | |
системы материальных точек где 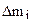 - масса i-й точки; - масса i-й точки; 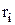 - расстояние этой точки от оси вращения; n – общее число материальных точек системы; - расстояние этой точки от оси вращения; n – общее число материальных точек системы; | 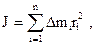 | |
| твердого тела | 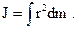 | |
Таблица 1
Моменты инерции некоторых тел правильной
геометрической формы
| Тело | Ось, относительно которой определяется момент инерции | Момент инерции |
| Однородный тонкий стержень массой m и длиной l | Проходит перпендикулярно стержню через его центр масс | 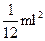 |
| Однородный тонкий стержень массой m и длиной l | Проходит перпендикулярно стержню через его конец | 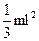  |
Продолжение таблицы 1
| Тонкое кольцо, обруч, труба радиусом R и массой m, равномерно распределенной по ободу | Проходит перпендикулярно плоскости основания через центр масс | 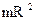 |
| Круглый однородный диск (цилиндр) радиусом R и массой m | Проходит перпендикулярно плоскости основания через центр масс | 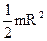 |
| Однородный шар массой m и радиусом R | Проходит через геометрический центр | 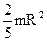 |
Момент импульса 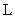 тела, вращающегося относительно неподвижной оси где J – момент инерции тела относительно этой же оси вращения, тела, вращающегося относительно неподвижной оси где J – момент инерции тела относительно этой же оси вращения, 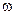 - угловая скорость. - угловая скорость. | 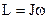 , , | ||
| Уравнение динамики вращательного движения твердого тела относительно неподвижной оси | 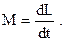 | ||
Если момент инерции тела не изменяется с течением времени, то уравнение динамики вращательного движения принимает вид: где 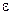 - угловое ускорение. - угловое ускорение. | 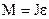 , , | ||
| Закон сохранения импульса для замкнутой системы где n - число материальных точек (тел), входящих в систему. | 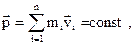 | ||
| Закон сохранения момента импульса для замкнутой системы | 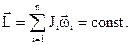 | ||
Элементарная работа силы где 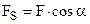 - проекция силы - проекция силы 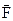 на направление перемещения на направление перемещения 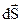 , , 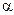 - угол между направлениями силы и перемещения. - угол между направлениями силы и перемещения. | 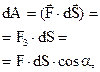 | ||
| Работа, совершаемая переменной силой, на пути S | 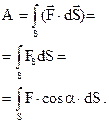 | ||
| Мгновенная мощность | 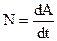 ; ; 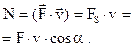 | ||
| Кинетическая энергия поступательного движения тела массы m | 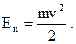 | ||
| Кинетическая энергия вращательного движения тела, имеющего момент инерции J, вокруг неподвижной оси | 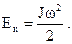 | ||
Кинетическая энергия катящегося тела: где 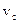 - скорость центра масс, - скорость центра масс, 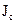 - момент инерции, относительно оси, проходящей через центр масс тела. - момент инерции, относительно оси, проходящей через центр масс тела. | 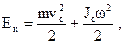 | ||
| Потенциальная энергия тела, поднятого над поверхностью Земли на высоту h где g - ускорение свободного падения. | 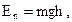 | ||
| Потенциальная энергия упруго деформированного тела где k - коэффициент упругой силы; х - абсолютная деформация. | 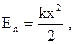 | ||
Уравнение гармонических колебаний где x - смещение колеблющейся точки от положения равновесия; t - время; 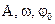 - соответственно амплитуда, круговая (циклическая) частота, начальная фаза колебаний; - соответственно амплитуда, круговая (циклическая) частота, начальная фаза колебаний; 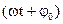 - фаза колебаний в момент времени t. - фаза колебаний в момент времени t. | 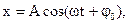 | ||
Круговая (циклическая) частота колебаний где 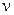 и T - частота и период колебаний. и T - частота и период колебаний. | 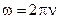 , , 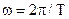 , , | ||
| Скорость точки, совершающей гармонические колебания | 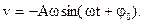 | ||
| Ускорение точки, совершающей гармонические колебания | 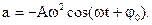 | ||
| Энергия материальной точки, совершающей гармонические колебания: | |||
кинетическая – 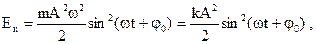 | |||
потенциальная – 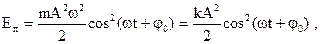 | |||
полная - 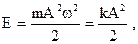 | |||
| где m - масса точки, k - коэффициент упругой (квазиупругой) силы. | |||
| Период колебаний тела, подвешенного на пружине (пружинный маятник) где m - масса тела, k - коэффициент жесткости пружины. | 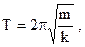 | ||
Период колебаний математического маятника где 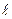 - длина маятника; g - ускорение свободного падения. - длина маятника; g - ускорение свободного падения. | 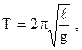 | ||
Период колебаний физического маятника где J - момент инерции колеблющегося тела относительно оси колебаний, а - расстояние центра масс маятника от оси колебаний; 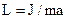 - приведенная длина физического маятника. - приведенная длина физического маятника. | 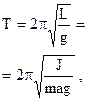 | ||
| Масса релятивистской частицы где m0 – масса покоя. | 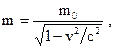 | ||
| Релятивистский импульс | 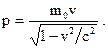 | ||
| Полная энергия релятивистской частицы | 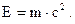 | ||
| Кинетическая энергия релятивистской частицы | 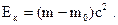 | ||
| Связь между энергией и импульсом релятивистской частицы | 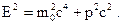 | ||
Количество вещества тела (системы) где N - число структурных элементов (молекул, атомов, ионов и т.п.), составляющих тело (систему); 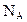 - постоянная Авогадро. - постоянная Авогадро. | 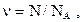 | ||
Молярная масса вещества где m - масса однородного тела (системы); 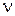 - количество вещества этого тела. - количество вещества этого тела. | 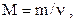 | ||
Молярная масса смеси газов где 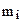 - масса i-го компонента смеси; - масса i-го компонента смеси; 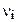 - количество вещества i -го компонента смеси; k - число компонентов смеси. - количество вещества i -го компонента смеси; k - число компонентов смеси. | 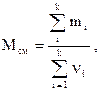 | ||
Уравнение состояния идеальных газов (уравнение Менделеева - Клапейрона) где m - масса газа; М- его молярная масса; R - молярная газовая постоянная; Т - термодинамическая температура; 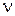 - количество вещества. - количество вещества. | 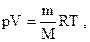 или или 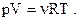 | ||
Закон Дальтона где р - давление смеси газов; 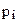 - парциальное давление i-го компонента смеси, k – число компонентов смеси. - парциальное давление i-го компонента смеси, k – число компонентов смеси. | 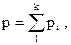 | ||
| Концентрация частиц (молекул, атомов и т.п.) однородной системы где N – число частиц, V - объем системы. | n=N/V , | ||
Основное уравнение молекулярно- кинетической теории газов где р - давление газа, n – концентрация молекул, 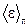 - средняя кинетическая энергия поступательного движения молекулы. - средняя кинетическая энергия поступательного движения молекулы. | 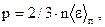 | ||
| Средняя кинетическая энергия приходящаяся на одну степень свободы молекулы | 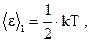 | ||
| поступательного движения молекулы | 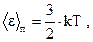 | ||
| вращательного движения молекулы | 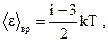 | ||
| приходящаяся на все степени свободы молекулы (полная энергия молекулы) | 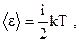 | ||
| где k - постоянная Больцмана; Т - термодинамическая температура; i - число степеней свободы молекулы. Для одноатомной молекулы i=3, для двухатомной i=5, для молекул, состоящих из трех и более атомов i=6. | |||
| Зависимость давления газа от концентрации молекул и температуры | p=nkT . | ||
| Скорости молекул газа | |||
| среднеквадратичная | 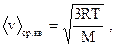 | ||
| средняя арифметическая | 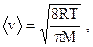 | ||
| наиболее вероятная | 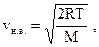 | ||
Внутренняя энергия идеального газа где 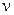 - количество вещества; m - масса газа; М - молярная масса газа; R - молярная газовая постоянная. - количество вещества; m - масса газа; М - молярная масса газа; R - молярная газовая постоянная. | 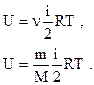 | ||
Первое начало термодинамики где Q - количество теплоты, полученное системой; 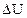 - изменение внутренней энергии системы; А - работа, совершенная системой против внешних сил. - изменение внутренней энергии системы; А - работа, совершенная системой против внешних сил. | 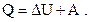 | ||
| Первое начало термодинамики для бесконечно малого изменения состояния системы | 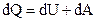 | ||
| Связь между молярной (Сm ) и удельной (с) теплоемкостями газа где М - молярная масса газа. | Сm = сМ , | ||
| Молярные теплоемкости газа | |||
| при постоянном объеме | 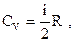 | ||
| при постоянном давлении | 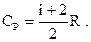 | ||
| Уравнение Майера где R - молярная газовая постоянная | СP = CV +R , | ||
| Показатель адиабаты | 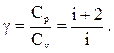 | ||
Уравнение адиабатного процесса (уравнение Пуассона) где 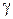 - показатель адиабаты - показатель адиабаты | 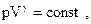 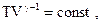 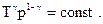 | ||
| Количество теплоты, полученное системой или отданное ею | |||
| при изохорном процессе | 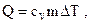 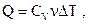 | ||
при изобарном процессе где 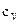 и и 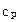 - удельные теплоемкости при постоянном объеме и давлении, а - удельные теплоемкости при постоянном объеме и давлении, а 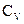 и и 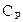 - соответствующие молярные теплоемкости, - соответствующие молярные теплоемкости, 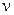 - количество вещества. - количество вещества. | 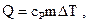 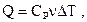 | ||
| Изменение внутренней энергии идеального газа | 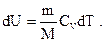 | ||
| Элементарная работа, совершаемая газом при изменении его объема | 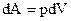 | ||
| Полная работа газа при изменении объема где V1 и V2 – соответственно начальный и конечный объемы газа. | 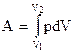 | ||
| Работа газа при изобарном процессе | 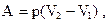 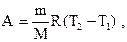 | ||
| при изотермическом процессе | 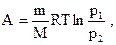 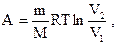 | ||
| при адиабатном процессе где Т1, Т2 и V1, V2 – соответственно начальные и конечные температуры и объемы газа. | 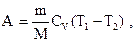 | ||
| Коэффициент полезного действия тепловой машины где Q1 – количество теплоты, полученное от нагревателя, Q2 – количество теплоты, отданное холодильнику. | 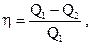 | ||
| Максимальный коэффициент полезного действия тепловой машины (КПД цикла Карно) где Т1 и Т2 – температуры нагревателя и холодильника, соответственно. | 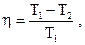 | ||
| Изменение энтропии системы при переходе из состояния 1 в состояние 2 | 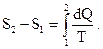 | ||
