Примеры к контрольной работе № 2

1. Какие из следующих функций являются бесконечно малыми, бесконечно большими при 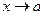(правило 2):

а) ;

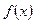имеет конечный предел при .

б) 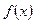является бесконечно большой при .

в) 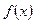является бесконечно малой при .

1. Найти пределы функций. Пользуемся правилами 1, 2, 3, 4, 5.

а) ,так как , , , .

б) .

При этом разложим квадратный трёхчлен в числителе на множители

, где и – корни, , ;

; ; .

В знаменателе , т.к. .

в) = Пусть , , =

.

г) Пусть , , =

.

1. Задана функция 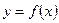. Найти точки разрыва функции, если они существуют. Сделать чертёж.

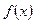– определена и непрерывна на всей числовой оси. Она может иметь разрывы в точках и . Найдем односторонние пределы (слева и справа) в этих точках.

; ; ; . Левый и правый пределы конечные, но не равны между собой; 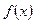имеет в точке конечный разрыв скачок равен .

; ; ; .Пределы слева и справа конечны и равны . В точке 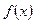– непрерывна.

Задания к контрольной работе № 2

Содержит 3 контрольных задания:

1) Какие из следующих функций являются бесконечно малыми и бесконечно большими при .

2) Найти пределы функции.

3) Задана функция . Найти точки разрыва функции, если они существуют. Сделать чертеж.

№ вар-та	Задания	№ вар-та	Задания
	1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) . 3)		1) а) ; б) ; в) . 2. а) ; б) ; в) ; г) . 3)
	1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) . 3)		1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) . 3)
	1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) 3)		1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) 3)
	1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) 3)		1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) . 3)
	1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) . 3)		1) а) ; б) ; в) . 2) а) ; б) ; в) ; г) . 3)

Контрольная работа № 3

Тема:Производные

Основные методические указания

1. Таблица основных производных

, – функции от х

с, а, const – постоянные числа,

1–1) ;

1–2)

1–3)

1–4)

1–5)

1–6)

1–7)

1–8)

1–9)

1–10)

1–11)

1–12)

2. Основные правила дифференцирования

2–1)

2–2)

2–3) (с – число)

2–4)

3. Производная функции, заданной параметрически

3–1)

4. Производные высших порядков , и так далее

Чтобы найти производную второго порядка , надо сначала найти первую производную и затем найти производную от полученной функции.

Примеры нахождения производных

1. ;

Применяем формулы 2–3, 1–3

,

2.

Применяем формулы 1–2, 1–8

3. ;

Применяем формулы 2–2, 1–2, 1–11

;

4.

Применяем формулы 2–4, 2–1, 1–7, 1–4

5.

Применяем формулы 3–1, 1–3, 1–5, 1–7, 1–2

;

6.

Найдем :

Применяем формулы 1–1, 1–2, 2–1

Применяем формулы 2–2, 2–3, 2–1, 1–1, 1–2

Задания к контрольной работе № 3

Контрольная работа содержит 6 заданий. В заданиях 1–5 надо найти производные функции , в задании 6 – найти вторую производную .

№ вар-та	Задания	№ вар-та	Задания
	1) ; 2) ; 3) ; 4) ; 5) ; 6) ;		1) ; 2) 3) ; 4) ; 5) ; 6)
	1) ; 2) ; 3) ; 4) ; 5) ; 6)		1) ; 2) ; 3) ; 4) ; 5) ; 6)
	1) ; 2) ; 3) ; 4) ; 5) ; 6)		1) ; 2) ; 3) ; 4) ; 5) ; 6)
	1) ; 2) ; 3) ; 4) ; 5) ; 6)		1) ; 2) ; 3) ; 4) ; 5) ; 6)
	1) ; 2) ; 3) ; 4) ; 5) ; 6)		1) ; 2) ; 3) ; 4) ; 5) ; 6)

Контрольная работа № 4