Исходные формы выявления и представления связей.

Удобной формой представления данных является корреляционная таблица. Пусть есть две случайные переменные X и Y, характеризующие какое-либо явление или процесс, между которыми надо изучить связь. Сначала надо произвести группировку каждой СВ, т.е. определить градации X и Y. Градации X записываются по горизонтали в верхней части таблицы, причем самая низшая градация записывается слева. Градации Y записываются по вертикали вдоль левого края таблицы, причем самая низшая градация записывается вверху. Горизонтальные и вертикальные линии, отделяющие различные градации, образуют клетки таблицы, в которые заносятся соответствующие этим интервалам изменения СВ частоты. Когда большинство частот группируется около диагонали от левого верхнего угла до правого нижнего, т.е. когда большим значениям X соответствуют большие значения Y , говорят, что две СВ коррелируют положительно. Если же большим значениям X соответствуют малые значения Y, то говорят, что СВ коррелируют отрицательно. В итоговых строках и столбцах таблицы дается два распределения: распределение по признаку X (нижняя строка – сумма частот по столбцам) и распределение по признаку Y (крайний правый столбец – сумма частот по строкам). На основе этих распределений можно рассчитать средние значения СВ 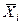и 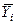для каждой градации.

Исходные данные, используемые для создания корреляционной таблицы, можно изобразить графически в виде точечной диаграммы– так называемого корреляционного поля (плоскости или решетки). По осям абсцисс и ординат откладываются интервалы изменения величин X и Y , а в двумерной плоскости каждой паре значений X и Y соответствует точка. По наибольшей плотности точек на корреляционной плоскости судят о форме корреляционной связи. Вообще, все значения случайных величин лежат внутри эллипса или окружности. Если по осям откладывать средние значения СВ X и Y , например, для центральных точек градаций Х_i откладывать 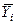, то получим эмпирическую линию регрессии .

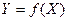Ниже на диаграммах представлены примеры корреляционных связей в поле корреляционных решеток:

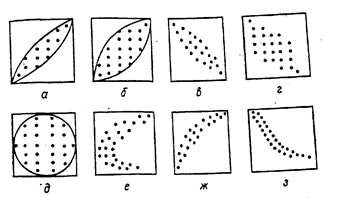
а – высокая положительная; б – средняя положительная; в – высокая отрицательная; г – средняя отрицательная; д – связь отсутствует; е – связь неопределенна; ж – криволинейная положительная; з – криволинейная отрицательная.

Когда большинство частот группируется около диагонали от левого нижнего угла до правого верхнего, т.е. когда большим значениям X соответствуют большие значения Y , говорят, что две СВ коррелируют положительно. Если же большим значениям X соответствуют малые значения Y, то говорят, что СВ коррелируют отрицательно. Когда все наблюдения попадают на прямую, тангенс угла наклона которой отличен от нуля или бесконечности, корреляция идеальная. Если все значения случайных величин лежат примерно внутри эллипса, главная ось которого расположена вертикально или горизонтально или внутри окружности, то это является признаком отсутствия корреляции. Если эллипс с наклонными осями – это признак слабой корреляции.

Следующая задача – проведение линии на графике, возможно ближе примыкающей к системе точек, нанесенных на плоскость (линии эмпирической регрессии) и подбора ее формулы. При выборе вида формулы весьма полезны альбомы кривых, которые приводятся в справочниках. Существуют также специальные методы приближенного определения параметров аппроксимирующей функции.